2.1: Integrals

We now turn our attention to the other side of Zeno's arrow paradox. In the previous chapter we began with the problem of finding the velocity of an object given a function which defined the position of the object at every instant of time. We now suppose that we are given a function which specifies the velocity \(v\) of an object, moving along a straight line, at every instant of time \(t,\) and we wish to find the position \(x\) of the object at time \(t .\) There are two approaches to finding \(x ;\) we will investigate both, leading us to the fundamental theorem of calculus.

First, from our earlier work we know that \(v\) is the derivative of \(x .\) That is, \[\frac{d x}{d t}=v .\] Hence to find \(x\) we need to find a function which has \(v\) for its derivative.

Definition

Given a function \(f\) defined on an open interval \((a, b),\) we call a function \(F\) an integral of \(f\) if \(F^{\prime}(x)=f(x)\) for all \(x\) in \((a, b)\).

Example \(\PageIndex{1}\)

If \(f(x)=3 x^{2},\) then \(F(x)=x^{3}\) is an integral of \(f\) on \((-\infty, \infty)\) since \(F^{\prime}(x)=3 x^{2}\) for all \(x .\) However, note that \(F\) is not the only integral of \(f:\) for other examples, both \(G(x)=x^{3}+4\) and \(H(x)=x^{3}+15\) are integrals of \(f\) as well. Indeed, since the derivative of a constant is 0 the function \(L(x)=x^{3}+c\) is an integral of \(f\) for any constant \(c .\)

In general, if \(F\) is an integral of \(f,\) then \(G(x)=F(x)+c\) is also an integral of \(f\) for any constant \(c\) Are there any other integrals of \(f ?\) That is, if we start with both \(F\) and \(G\) being integrals of \(f,\) does it follow that \(G(x)-F(x)=c\) for some constant \(c\) and for all \(x ?\) To answer this question, first note that if we let \(H(x)=G(x)-F(x),\) then

\[H^{\prime}(x)=G^{\prime}(x)-F^{\prime}(x)=f(x)-f(x)=0\] for all \(x .\) Hence \(H\) is an integral of the constant function \(g(x)=0\) for all \(x .\) So our question becomes: If \(H^{\prime}(x)=0\) for all \(x,\) does it follow that \(H(x)=c\) for some constant \(c\) and all \(x ?\) If it does, then \[c=H(x)=F(x)-G(x) ,\] and indeed \(F\) and \(G\) differ by only a constant. So suppose we are given \(H^{\prime}(x)=0\) for all \(x\) in an open interval \((a, b) .\) Then, for any two points \(u<v\) in \((a, b),\) it follows from the mean-value theorem that \[H(v)-H(u)=H^{\prime}(d)(u-v)\] for some \(d\) in \((a, b) .\) But then \(H^{\prime}(d)=0,\) so \(H(v)-H(u)=0,\) that is, \(H(u)=\) \(H(v) .\) Since this is true for any arbitrary points \(u\) and \(v\) in \((a, b),\) it follows that \(H\) must be constant on \((a, b) .\)

Theorem \(\PageIndex{1}\)

If \(F^{\prime}(x)=G^{\prime}(x)\) for all \(x\) in \((a, b),\) then there exists a constant \(c\) such that \(G(x)=F(x)+c\) for all \(x\) in \((a, b)\).

In particular, if \(F^{\prime}(x)=0\) for all \(x\) in \((a, b),\) then \(F\) is constant on \((a, b)\).

Example \(\PageIndex{2}\)

Since

\[\frac{d}{d x}\left(\frac{3}{2} x^{2}+4 x\right)=3 x+4 ,\] any integral of \(f(x)=3 x+4\) must be of the form \[F(x)=\frac{3}{2} x^{2}+4 x+c\] for some constant \(c\).

We denote an integral of a function \(f\) by

\[\int f(x) d x .\]

The motivation for this notation will be more evident once we discuss the fundamental theorem of calculus.

Example \(\PageIndex{3}\)

Since

\[\frac{d}{d x}\left(4 x^{3}-\sin (x)\right)=12 x^{2}-\cos (x),\]

it follows that \[\int\left(12 x^{2}-\cos (x)\right) d x=4 x^{3}-\sin (x)+c ,\] where, as before, \(c\) is some constant.

From our rules for differentiation, it follows easily that

\[\int x^{n} d x=\frac{1}{n+1} x^{n+1}+c\] or every rational \(n \neq-1,\) and \[\int \sin (x) d x=-\cos (x)+c ,\] \[\int \cos (x) d x=\sin (x)+c ,\] \[\int \sec ^{2}(x) d x=\tan (x)+c ,\] \[\int \csc ^{2}(x) d x=-\csc (x)+c ,\] \[\int \sec (x) \tan (x) d x=\sec (x)+c ,\] and \[\int \csc (x) \cot (x) d x=-\csc (x)+c ,\] where in each case \(c\) represents an arbitrary constant. Note that differentiation of the right-hand side of each of the above verifies these statements. Moreover, if follows from our work with derivatives that for any functions \(f\) and \(g\) and any constant \(k\), \[\int(f(x)+g(x)) d x=\int f(x) d x+\int g(x) d x ,\] \[\int(f(x)-g(x)) d x=\int f(x) d x-\int g(x) d x ,\] and \[\int k f(x) d x=k \int f(x) d x .\]

Example \(\PageIndex{4}\)

\[\int\left(5 x^{3}-6 x+8\right) d x=\frac{5}{4} x^{4}-3 x^{2}+8 x+c .\]

Example \(\PageIndex{5}\)

\[\int(\sin (x)-4 \cos (x)) d x=-\cos (x)-4 \sin (x)+c .\]

Example \(\PageIndex{6}\)

Making an adjustment for the chain rule, we see that

\[\int \sin (5 x) d x=-\frac{1}{5} \cos (5 x)+c .\]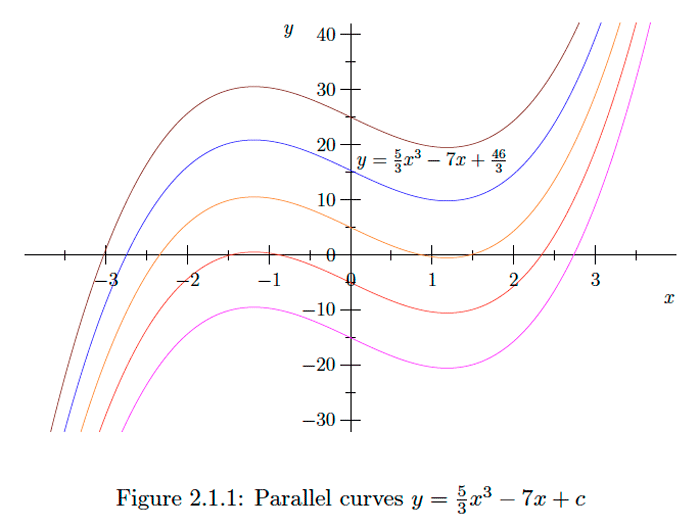

Example \(\PageIndex{7}\)

Suppose we wish to find the integral \(F(x)\) of \(f(x)=5 x^{2}-7\) for which \(F(1)=10 .\) Now

\[\int\left(5 x^{2}-7\right) d x=\frac{5}{3} x^{3}-7 x+c ,\] so \[F(x)=\frac{5}{3} x^{3}-7 x+c \] for some constant \(c .\) Now we want \[10=F(1)=\frac{5}{3}-7+c ,\] so we must have \[c=10+7-\frac{5}{3}=\frac{46}{3} .\] Hence the desired integral is \[F(x)=\frac{5}{3} x^{3}-7 x+\frac{46}{3} .\] Note that, geometrically, from the family of parallel curves with equations of the form \(y=\frac{5}{3} x^{3}-7 x+c,\) we are finding the one that passes through the point \((1,10) .\) Figure 2.1 .1 shows five such curves, with the graph of \(F\) in blue.

Exercise \(\PageIndex{1}\)

Evaluate each of the following:

\[\begin{array}{ll}{\text { (a) } \int\left(x^{2}+3\right) d x} & {\text { (b) } \int \frac{1}{x^{2}} d x} \\ {\text { (c) } \int(3 \sin (x)-5 \sec (x) \tan (x)) d x} & {\text { (d) } \int 4 \sqrt{x} d x}\end{array} \]

Answer

(a) \(\int\left(x^{2}+3\right) d x=\frac{1}{3} x^{3}+3 x+c\)

(b) \(\int \frac{1}{x^{2}} d x=-\frac{1}{x}+c\)

(c) \(\int(3 \sin (x)-5 \sec (x) \tan (x)) d x=-3 \cos (x)-5 \sec (x)+c\)

(d) \(\int 4 \sqrt{x} d x=6 x^{\frac{3}{2}}+c\)

Exercise \(\PageIndex{2}\)

Find an integral \(F\) of \(f(x)=5 x^{4}-4 x\) which satisfies \(F(2)=12\).

Answer

\(F(x)=x^{5}-2 x^{2}-12\)

Returning to our original problem, we can now say that if \(v(t)\) is, at time \(t,\) the velocity of an object moving along a straight line and \(x(t)\) is the object's position at time \(t\), then

\[x(t)=\int v(t) d t \] However, note that \((2.1 .16)\) is little more than a restatement of \((2.1 .1)\) with new notation.

Example \(\PageIndex{8}\)

Suppose the velocity of an object oscillating at the end of a spring is

\[v(t)=-20 \sin (5 t) \text { centimeters / second. } \] If \(x(t)\) is the position of the object at time \(t,\) then \[x(t)=-\int 20 \sin (5 t) d t=4 \cos (5 t)+c \text { centimeters } \] for some constant \(c .\) If in addition we know that the object was initially 4 centimeters from the origin, that is, that \(x(0)=4,\) then we would have \[4=x(0)=4+c .\] Hence we would have \(c=0,\) and so \[x(t)=4 \cos (5 t) \text { centimeters } \] completely specifies the position of the object at time \(t .\)

Exercise \(\PageIndex{3}\)

Suppose the velocity of an object at time \(t\) is \(v(t)=10 \sin (t)\) centimeters per second. Find \(x(t),\) the position of the object at time \(t,\) if \(x(0)=\) 10 centimeters.

Answer

\(x(t)=-10 \cos (t)+20\)

2.1.1 The Case of Constant Acceleration

Galileo was the first to notice that, ignoring the effects of air resistance, objects in free fall near the surface of the earth fall with constant acceleration. Suppose that \(x(t), v(t),\) and \(a(t)\) specify, at time \(t,\) the position, velocity, and acceleration of an object moving along a straight line, and, moreover, suppose

\[a(t)=g\] for some constant \(g\) and all values of \(t .\) Since acceleration is the derivative of velocity, it follows that \[v(t)=\int a(t) d t=\int g d t=g t+c \] for some constant \(c .\) Now if we let \(v_{0}=v(0),\) the velocity of the object at time \(t=0,\) then \[v_{0}=v(0)=c .\] Hence \[v(t)=g t+v_{0} .\] Next we see that \[x(t)=\int v(t) d t=\int\left(g t+v_{0}\right) d t=\frac{1}{2} g t^{2}+v_{0} t+c \] for some constant \(c .\) If we let \(x_{0}=x(0),\) the position of the object at time \(t=0,\) then \[x_{0}=x(0)=c .\] Hence we have \[x(t)=\frac{1}{2} g t^{2}+v_{0} t+x_{0} .\] In the important case of an object in free fall near the surface of the earth, \(g\) is the constant acceleration due to gravity. When working in units of meters and seconds, and taking up as the positive direction, we have \(g=-9.8\) meters per second per second, and when working with units of feet and seconds \(g=-32\) feet per second per second. Hence, in the former case, \((2.1 .23)\) becomes \[x(t)=-4.9 t^{2}+v_{0} t+x_{0}\] and, in the latter case, \((2.1 .23)\) becomes \[x(t)=-16 t^{2}+v_{0} t+x_{0}.\]

Example \(\PageIndex{9}\)

Suppose an object is thrown upward from atop a 10 meter tall tower with an initial velocity of 20 meters per second. Then, using \((2.1 .24),\) the position of the object after \(t\) seconds is

\[x(t)=-4.9 t^{2}+20 t+10 \text { meters. }\] Hence, for example, since the object will reach its maximum height when its velocity is \(0,\) we see that the object reaches its maximum height when \[-9.8 t+20=0 ,\] that is, when \[t=\frac{20}{9.8} \approx 2.04 \text { seconds. }\] Thus the object will reach a maximum height of \[x(2.04) \approx-4.9(2.04)^{2}+20(2.04)+10 \approx 30.41 \text { meters. }\]

Exercise \(\PageIndex{4}\)

For an object in free-fall near the surface of Mars, \(g=-3.69\) meters per second per second. Find the maximum height reached by an object thrown vertically into the air from atop a 10 meter tall tower on Mars with an initial velocity of 20 meters per second.

Answer

64.20 meters