2.R: Chapter 2 Review Exercises

Last updated
Save as PDF

Page ID: 50411

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

True or False. In exercises 1 - 4, justify your answer with a proof or a counterexample.

1) A function has to be continuous at $x=a$ if the $\displaystyle \lim_{x→a}f(x)$ exists.

2) You can use the quotient rule to evaluate $\displaystyle \lim_{x→0}\frac{\sin x}{x}$.

Answer: False, since we cannot have $\displaystyle \lim_{x→0}x=0$ in the denominator.

3) If there is a vertical asymptote at $x=a$ for the function $f(x)$, then $f$ is undefined at the point $x=a$.

4) If $\displaystyle \lim_{x→a}f(x)$ does not exist, then $f$ is undefined at the point $x=a$.

Answer: False. A jump discontinuity is possible.

5) Using the graph, find each limit or explain why the limit does not exist.

a. $\displaystyle \lim_{x→−1}f(x)$

b. $\displaystyle \lim_{x→1}f(x)$

c. $\displaystyle \lim_{x→0^+}f(x)$

d. $\displaystyle \lim_{x→2}f(x)$

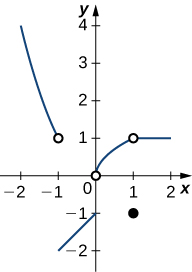
$A graph of a piecewise function with several segments. The first is a decreasing concave up curve existing for x < -1. It ends at an open circle at (-1, 1). The second is an increasing linear function starting at (-1, -2) and ending at (0,-1). The third is an increasing concave down curve existing from an open circle at (0,0) to an open circle at (1,1). The fourth is a closed circle at (1,-1). The fifth is a line with no slope existing for x > 1, starting at the open circle at (1,1).$

In exercises 6 - 15, evaluate the limit algebraically or explain why the limit does not exist.

6) $\displaystyle \lim_{x→2}\frac{2x^2−3x−2}{x−2}$

Answer: $5$

7) $\displaystyle \lim_{x→0}3x^2−2x+4$

8) $\displaystyle \lim_{x→3}\frac{x^3−2x^2−1}{3x−2}$

Answer: $8/7$

9) $\displaystyle \lim_{x→π/2}\frac{\cot x}{\cos x}$

10) $\displaystyle \lim_{x→−5}\frac{x^2+25}{x+5}$

Answer: DNE

11) $\displaystyle \lim_{x→2}\frac{3x^2−2x−8}{x^2−4}$

12) $\displaystyle \lim_{x→1}\frac{x^2−1}{x^3−1}$

Answer: $2/3$

13) $\displaystyle \lim_{x→1}\frac{x^2−1}{\sqrt{x}−1}$

14) $\displaystyle \lim_{x→4}\frac{4−x}{\sqrt{x}−2}$

Answer: $−4$

15) $\displaystyle \lim_{x→4}\frac{1}{\sqrt{x}−2}$

In exercises 16 - 17, use the squeeze theorem to prove the limit.

16) $\displaystyle \lim_{x→0}x^2\cos(2πx)=0$

Answer: Since $−1≤\cos(2πx)≤1$, then $−x^2≤x^2\cos(2πx)≤x^2$. Since $\displaystyle \lim_{x→0}x^2=0=\lim_{x→0}−x^2$, it follows that $\displaystyle \lim_{x→0}x^2\cos(2πx)=0$.

17) $\displaystyle \lim_{x→0}x^3\sin\left(\frac{π}{x}\right)=0$

18) Determine the domain such that the function $f(x)=\sqrt{x−2}+xe^x$ is continuous over its domain.

Answer: $[2,∞]$

In exercises 19 - 20, determine the value of $c$ such that the function remains continuous. Draw your resulting function to ensure it is continuous.

19) $f(x)=\begin{cases}x^2+1, & \text{if } x>c\\2^x, & \text{if } x≤c\end{cases}$

20) $f(x)=\begin{cases}\sqrt{x+1}, & \text{if } x>−1\\x^2+c, & \text{if } x≤−1\end{cases}$

In exercises 21 - 22, use the precise definition of limit to prove the limit.

21) $\displaystyle \lim_{x→1}\,(8x+16)=24$

22) $\displaystyle \lim_{x→0}x^3=0$

Answer: $δ=\sqrt[3]{ε}$

23) A ball is thrown into the air and the vertical position is given by $x(t)=−4.9t^2+25t+5$. Use the Intermediate Value Theorem to show that the ball must land on the ground sometime between 5 sec and 6 sec after the throw.

24) A particle moving along a line has a displacement according to the function $x(t)=t^2−2t+4$, where $x$ is measured in meters and $t$ is measured in seconds. Find the average velocity over the time period $t=[0,2]$.

Answer: $0$ m/sec

25) From the previous exercises, estimate the instantaneous velocity at $t=2$ by checking the average velocity within $t=0.01$ sec.

Search

Text Color

Text Size

Margin Size

Font Type