15.7E: Exercises for Section 15.7
( \newcommand{\kernel}{\mathrm{null}\,}\)
In exercises 1 - 6, the function T : S \rightarrow R, \space T (u,v) = (x,y) on the region S = \big\{(u,v) \,|\, 0 \leq u \leq 1, \space 0 \leq v \leq 1\big\} bounded by the unit square is given, where R \in R^2 is the image of S under T.
a. Justify that the function T is a C^1 transformation.
b. Find the images of the vertices of the unit square S through the function T.
c. Determine the image R of the unit square S and graph it.
1. x = 2u, \space y = 3v
2. x = \frac{u}{2}, \space y = \frac{v}{3}
- Answer
-
a. T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = \frac{u}{2} and y = h(u,v) = \frac{v}{3}. The functions g and h are continuous and differentiable, and the partial derivatives g_u (u,v) = \frac{1}{2}, \space g_v (u,v) = 0, \space h_u (u,v) = 0 and h_v (u,v) = \frac{1}{3} are continuous on S;
b. T(0,0) = (0,0), \space T(1,0) = \left(\frac{1}{2},0\right), \space T(0,1) = \left(0,\frac{1}{3}\right), and T(1,1) = \left(\frac{1}{2}, \frac{1}{3} \right);
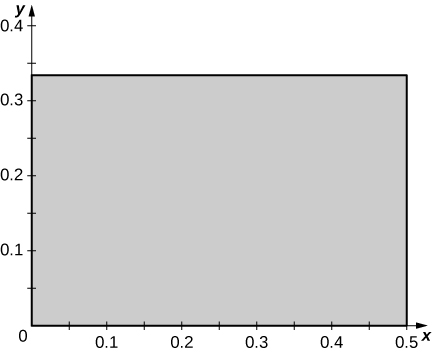
c. R is the rectangle of vertices (0,0), \space \left(0,\frac{1}{3}\right), \space \left(\frac{1}{2}, \frac{1}{3} \right), and \left(0,\frac{1}{3}\right) in the xy-plane; the following figure.
3. x = u - v, \space y = u + v
4. x = 2u - v, \space y = u + 2v
- Answer
-
a. T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = 2u - v and y = h(u,v) = u + 2v. The functions g and h are continuous and differentiable, and the partial derivatives g_u (u,v) = 2, \space g_v (u,v) = -1, \space h_u (u,v) = 1 and h_v (u,v) = 2 are continuous on S;
b. T(0,0) = (0,0), \space T(1,0) = (2,1), \space T(0,1) = (-1,2), and T(1,1) = (1,3);
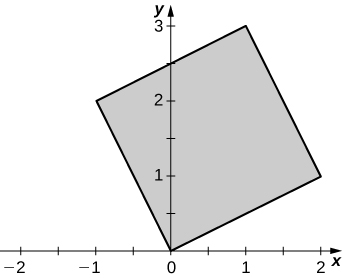
c. R is the parallelogram of vertices (0,0), \space (2,1) \space (1,3), and (-1,2) in the xy-plane; the following figure.
5. x = u^2, \space y = v^2
6. x = u^3, \space y = v^3
- Answer
-
a. T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = u^3 and y = h(u,v) = v^3. The functions g and h are continuous and differentiable, and the partial derivatives g_u (u,v) = 3u^2, \space g_v (u,v) = 0, \space h_u (u,v) = 0 and h_v (u,v) = 3v^2 are continuous on S;
b. T(0,0) = (0,0), \space T(1,0) = (1,0), \space T(0,1) = (0,1), and T(1,1) = (1,1);
c. R is the unit square in the xy-plane see the figure in the answer to the previous exercise.
In exercises 7 - 12, determine whether the transformations T : S \rightarrow R are one-to-one or not.
7. x = u^2, \space y = v^2, where S is the rectangle of vertices (-1,0), \space (1,0), \space (1,1), and (-1,1).
8. x = u^4, \space y = u^2 + v, where S is the triangle of vertices (-2,0), \space (2,0), and (0,2).
- Answer
- T is not one-to-one: two points of S have the same image. Indeed, T(-2,0) = T(2,0) = (16,4).
9. x = 2u, \space y = 3v, where S is the square of vertices (-1,1), \space (-1,-1), \space (1,-1), and (1,1).
10. T(u, v) = (2u - v, u), where S is the triangle with vertices (-1,1), \, (-1,-1), and (1,-1).
- Answer
- T is one-to-one: We argue by contradiction. T(u_1,v_1) = T(u_2,v_2) implies 2u_1 - v_1 = 2u_2 - v_2 and u_1 = u_2. Thus, u_1 = u+2 and v_1 = v_2.
11. x = u + v + w, \space y = u + v, \space z = w, where S = R = R^3.
12. x = u^2 + v + w, \space y = u^2 + v, \space z = w, where S = R = R^3.
- Answer
- T is not one-to-one: T(1,v,w) = (-1,v,w)
In exercises 13 - 18, the transformations T : R \rightarrow S are one-to-one. Find their related inverse transformations T^{-1} : R \rightarrow S.
13. x = 4u, \space y = 5v, where S = R = R^2.
14. x = u + 2v, \space y = -u + v, where S = R = R^2.
- Answer
- u = \frac{x-2y}{3}, \space v= \frac{x+y}{3}
15. x = e^{2u+v}, \space y = e^{u-v}, where S = R^2 and R = \big\{(x,y) \,|\, x > 0, \space y > 0\big\}
16. x = \ln u, \space y = \ln(uv), where S = \big\{(u,v) \,|\, u > 0, \space v > 0\big\} and R = R^2.
- Answer
- u = e^x, \space v = e^{-x+y}
17. x = u + v + w, \space y = 3v, \space z = 2w, where S = R = R^3.
18. x = u + v, \space y = v + w, \space z = u + w, where S = R = R^3.
- Answer
- u = \frac{x-y+z}{2}, \space v = \frac{x+y-z}{2}, \space w = \frac{-x+y+z}{2}
In exercises 19 - 22, the transformation T : S \rightarrow R, \space T (u,v) = (x,y) and the region R \subset R^2 are given. Find the region S \subset R^2.
19. x = au, \space y = bv, \space R = \big\{(x,y) \,|\, x^2 + y^2 \leq a^2 b^2\big\} where a,b > 0
20. x = au, \space y = bc, \space R = \big\{(x,y) \,|\, \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1\big\}, where a,b > 0
- Answer
- S = \big\{(u,v) \,|\, u^2 + v^2 \leq 1\big\}
21. x = \frac{u}{a}, \space y = \frac{v}{b}, \space z = \frac{w}{c}, \space R = \big\{(x,y)\,|\,x^2 + y^2 + z^2 \leq 1\big\}, where a,b,c > 0
22. x = au, \space y = bv, \space z = cw, \space R = \big\{(x,y)\,|\,\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} \leq 1, \space z > 0\big\}, where a,b,c > 0
- Answer
- R = \big\{(u,v,w)\,|\,u^2 - v^2 - w^2 \leq 1, \space w > 0\big\}
In exercises 23 - 32, find the Jacobian J of the transformation.
23. x = u + 2v, \space y = -u + v
24. x = \frac{u^3}{2}, \space y = \frac{v}{u^2}
- Answer
- \frac{3}{2}
25. x = e^{2u-v}, \space y = e^{u+v}
26. x = ue^v, \space y = e^{-v}
- Answer
- -1
27. x = u \space \cos (e^v), \space y = u \space \sin(e^v)
28. x = v \space \sin (u^2), \space y = v \space \cos(u^2)
- Answer
- 2uv
29. x = u \space \cosh v, \space y = u \space \sinh v, \space z = w
30. x = v \space \cosh \left(\frac{1}{u}\right), \space y = v \space \sinh \left(\frac{1}{u}\right), \space z = u + w^2
- Answer
- \frac{v}{u^2}
31. x = u + v, \space y = v + w, \space z = u
32. x = u - v, \space y = u + v, \space z = u + v + w
- Answer
- 2
33. The triangular region R with the vertices (0,0), \space (1,1), and (1,2) is shown in the following figure.
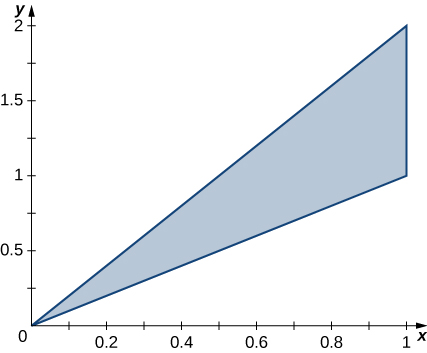
a. Find a transformation T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv), where a,b,c, and d are real numbers with ad - bc \neq 0 such that T^{-1} (0,0) = (0,0), \space T^{-1} (1,1) = (1,0), and T^{-1}(1,2) = (0,1).
b. Use the transformation T to find the area A(R) of the region R.
34. The triangular region R with the vertices (0,0), \space (2,0), and (1,3) is shown in the following figure.
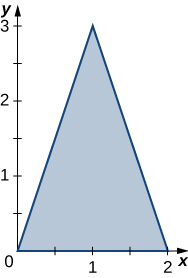
a. Find a transformation T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv), where a,b,c, and d are real numbers with ad - bc \neq 0 such that T^{-1} (0,0) = (0,0), \space T^{-1} (2,0) = (1,0), and T^{-1}(1,3) = (0,1).
b. Use the transformation T to find the area A(R) of the region R.
- Answer
-
a. T (u,v) = (2u + v, \space 3v)
b. The area of R is \displaystyle A(R) = \int_0^3 \int_{y/3}^{(6-y)/3} \, dx \, dy = \int_0^1 \int_0^{1-u} \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \, dv \space du = \int_0^1 \int_0^{1-u} 6 \, dv \, du = 3.
In exercises 35 - 36, use the transformation u = y - x, v = y, to evaluate the integrals on the parallelogram R of vertices (0,0), (1,0), (2,1) , and (1,1) shown in the following figure.
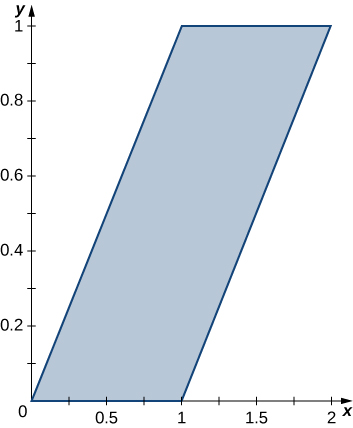
35. \displaystyle \iint_R (y - x) \, dA
36. \displaystyle \iint_R (y^2 - xy) \, dA
- Answer
- -\frac{1}{4}
In exercises 37 - 38, use the transformation y = x = u, x + y = v to evaluate the integrals on the square R determined by the lines y = x, y = -x + 2, y = x + 2, and y = -x shown in the following figure.
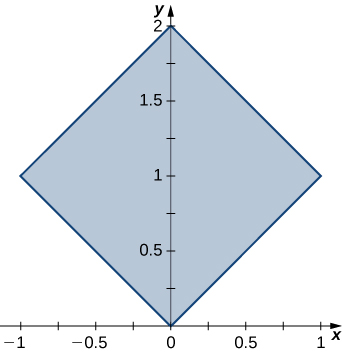
37. \displaystyle \iint_R e^{x+y} \, dA
38. \displaystyle \iint_R \sin (x - y) \, dA
- Answer
- -1 + \cos 2
In exercises 39 - 40, use the transformation x = u, 5y = v to evaluate the integrals on the region R bounded by the ellipse x^2 + 25y^2 = 1 shown in the following figure.
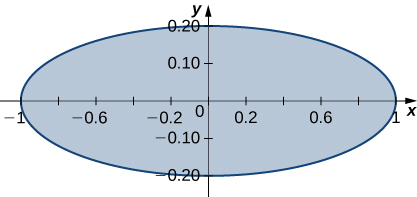
39. \displaystyle \iint_R \sqrt{x^2 + 25y^2} \, dA
40. \displaystyle \iint_R (x^2 + 25y^2)^2 \, dA
- Answer
- \frac{\pi}{15}
In exercises 41 - 42, use the transformation u = x + y, v = x - y to evaluate the integrals on the trapezoidal region R determined by the points (1,0), (2,0), (0,2), and (0,1) shown in the following figure.
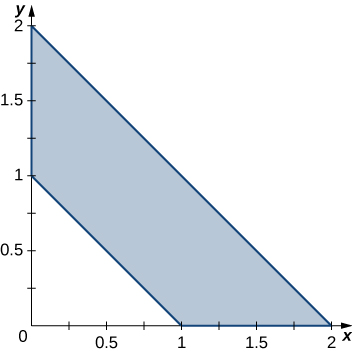
41. \displaystyle \iint_R (x^2 - 2xy + y^2) \space e^{x+y} \, dA
42. \displaystyle \iint_R (x^3 + 3x^2y + 3xy^2 + y^3) \, dA
- Answer
- \frac{31}{5}
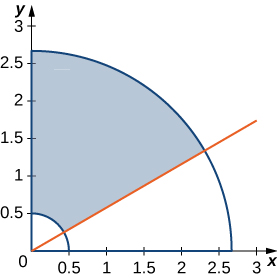
43. The circular annulus sector R bounded by the circles 4x^2 + 4y^2 = 1 and 9x^2 + 9y^2 = 64, the line x = y \sqrt{3}, and the y-axis is shown in the following figure. Find a transformation T from a rectangular region S in the r\theta-plane to the region R in the xy-plane. Graph S.
44. The solid R bounded by the circular cylinder x^2 + y^2 = 9 and the planes z = 0, \space z = 1, \space x = 0, and y = 0 is shown in the following figure. Find a transformation T from a cylindrical box S in r\theta z-space to the solid R in xyz-space.
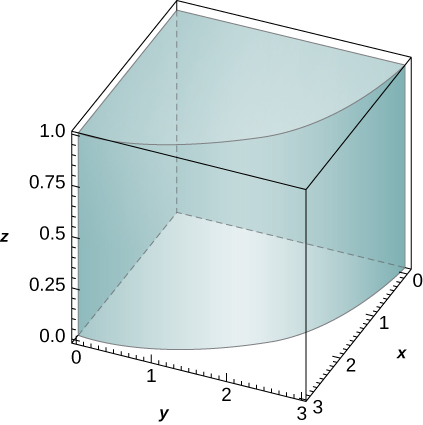
- Answer
- T (r,\theta,z) = (r \space \cos \theta, \space r \space \sin \theta, \space z); \space S = [0,3] \times [0,\frac{\pi}{2}] \times [0,1] in the r\theta z-space
45. Show that \iint_R f \left(\sqrt{\frac{x^2}{3} + \frac{y^2}{3}}\right) dA = 2 \pi \sqrt{15} \int_0^1 f (\rho) \rho \space d\rho, \nonumber where f is a continuous function on [0,1] and R is the region bounded by the ellipse 5x^2 + 3y^2 = 15.
46. Show that \iiint_R f \left(\sqrt{16x^2 + 4y^2 + z^2}\right) dV = \frac{\pi}{2} \int_0^1 f (\rho) \rho^2 d\rho, \nonumber where f is a continuous function on [0,1] and R is the region bounded by the ellipsoid 16x^2 + 4y^2 + z^2 = 1.
47. [T] Find the area of the region bounded by the curves xy = 1, \space xy = 3, \space y = 2x, and y = 3x by using the transformation u = xy and v = \frac{y}{x}. Use a computer algebra system (CAS) to graph the boundary curves of the region R.
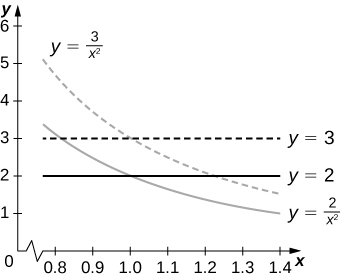
48. [T] Find the area of the region bounded by the curves x^2y = 2, \space x^2y = 3, \space y = x, and y = 2x by using the transformation u = x^2y and v = \frac{y}{x}. Use a CAS to graph the boundary curves of the region R.
- Answer
-
The area of R is 10 - 4\sqrt{6}; the boundary curves of R are graphed in the following figure.
49. Evaluate the triple integral \int_0^1 \int_1^2 \int_z^{z+1} (y + 1) \space dx \space dy \space dz \nonumber by using the transformation u = x - z, \space v = 3y, and w = \frac{z}{2}.
50. Evaluate the triple integral \int_0^2 \int_4^6 \int_{3z}^{3z+2} (5 - 4y) \space dx \space dy \space dz \nonumber by using the transformation u = x - 3z, \space v = 4y, and w = z.
- Answer
- 8
51. A transformation T : R^2 \rightarrow R^2, \space T (u,v) = (x,y) of the form x = au + bv, \space y = cu + dv, where a,b,c, and d are real numbers, is called linear. Show that a linear transformation for which ad - bc \neq 0 maps parallelograms to parallelograms.
52. A transformation T_{\theta} : R^2 \rightarrow R^2, \space T_{\theta} (u,v) = (x,y) of the form x = u \space \cos \theta - v \space \sin \theta, \space y = u \space \sin \theta + v \space \cos \theta, is called a rotation angle \theta. Show that the inverse transformation of T_{\theta} satisfies T_{\theta}^{-1} = T_{-\theta} where T_{-\theta} is the rotation of angle -\theta.
53. [T] Find the region S in the uv-plane whose image through a rotation of angle \frac{\pi}{4} is the region R enclosed by the ellipse x^2 + 4y^2 = 1. Use a CAS to answer the following questions.
a. Graph the region S.
b. Evaluate the integral \displaystyle \iint_S e^{-2uv} \, du \, dv. Round your answer to two decimal places.
54. [T] The transformations T_i : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space i = 1, . . . , 4, defined by T_1(u,v) = (u,-v), \space T_2 (u,v) = (-u,v), \space T_3 (u,v) = (-u, -v), and T_4 (u,v) = (v,u) are called reflections about the x-axis, y-axis origin, and the line y = x, respectively.
a. Find the image of the region S = \big\{(u,v)\,|\,u^2 + v^2 - 2u - 4v + 1 \leq 0\big\} in the xy-plane through the transformation T_1 \circ T_2 \circ T_3 \circ T_4.
b. Use a CAS to graph R.
c. Evaluate the integral \displaystyle \iint_S \sin (u^2) \, du \, dv by using a CAS. Round your answer to two decimal places.
- Answer
-
a. R = \big\{(x,y)\,|\,y^2 + x^2 - 2y - 4x + 1 \leq 0\big\};
b. R is graphed in the following figure;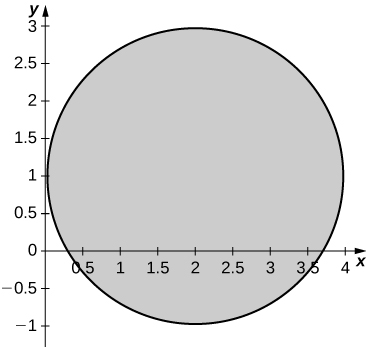
c. 3.16
55. [T] The transformations T_{k,1,1} : \mathbb{R}^3 \rightarrow \mathbb{R}^3, \space T_{k,1,1}(u,v,w) = (x,y,z) of the form x = ku, \space y = v, \space z = w, where k \neq 1 is a positive real number, is called a stretch if k > 1 and a compression if 0 < k < 1 in the x-direction. Use a CAS to evaluate the integral \displaystyle \iiint_S e^{-(4x^2+9y^2+25z^2)} \, dx \, dy \, dz on the solid S = \big\{(x,y,z) \,|\, 4x^2 + 9y^2 + 25z^2 \leq 1\big\} by considering the compression T_{2,3,5}(u,v,w) = (x,y,z) defined by x = \frac{u}{2}, \space y = \frac{v}{3}, and z = \frac{w}{5}. Round your answer to four decimal places.
56. [T] The transformation T_{a,0} : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space T_{a,0} (u,v) = (u + av, v), where a \neq 0 is a real number, is called a shear in the x-direction. The transformation, T_{b,0} : R^2 \rightarrow R^2, \space T_{o,b}(u,v) = (u,bu + v), where b \neq 0 is a real number, is called a shear in the y-direction.
a. Find transformations T_{0,2} \circ T_{3,0}.
b. Find the image R of the trapezoidal region S bounded by u = 0, \space v = 0, \space v = 1, and v = 2 - u through the transformation T_{0,2} \circ T_{3,0}.
c. Use a CAS to graph the image R in the xy-plane.
d. Find the area of the region R by using the area of region S.
- Answer
-
a. T_{0,2} \circ T_{3,0}(u,v) = (u + 3v, 2u + 7v);
b. The image S is the quadrilateral of vertices (0,0), \space (3,7), \space (2,4), and (4,9);
c. S is graphed in the following figure;
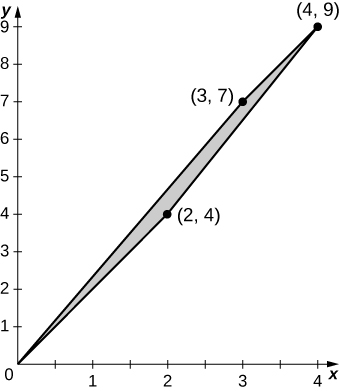
d. \frac{3}{2}
57. Use the transformation, x = au, \space y = av, \space z = cw and spherical coordinates to show that the volume of a region bounded by the spheroid \frac{x^2+y^2}{a^2} + \frac{z^2}{c^2} = 1 is \frac{4\pi a^2c}{3}.
58. Find the volume of a football whose shape is a spheroid \frac{x^2+y^2}{a^2} + \frac{z^2}{c^2} = 1 whose length from tip to tip is 11 inches and circumference at the center is 22 inches. Round your answer to two decimal places.
- Answer
- \frac{2662}{3\pi} \approx 282.45 \space in^3
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.

