16.8E: Exercises for Section 16.8
- Page ID
- 67036
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For exercises 1 - 9, use a computer algebraic system (CAS) and the divergence theorem to evaluate surface integral \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds\) for the given choice of \(\vecs F\) and the boundary surface \(S\). For each closed surface, assume \(\vecs N\) is the outward unit normal vector.
1. [T] \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\); \(S\) is the surface of cube \(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1\).
2. [T] \(\vecs F(x,y,z) = (\cos yz) \,\mathbf{\hat i} + e^{xz}\,\mathbf{\hat j} + 3z^2 \,\mathbf{\hat k}\); \(S\) is the surface of hemisphere \(z = \sqrt{4 - x^2 - y^2}\) together with disk \(x^2 + y^2 \leq 4\) in the \(xy\)-plane.
- Answer
- \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 75.3982\)
3. [T] \(\vecs F(x,y,z) = (x^2 + y^2 - x^2)\,\mathbf{\hat i} + x^2 y\,\mathbf{\hat j} + 3z\,\mathbf{\hat k}; \) \(S\) is the surface of the five faces of unit cube \(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 < z \leq 1.\)
4. [T] \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}; \) \(S\) is the surface of paraboloid \(z = x^2 + y^2\) for \(0 \leq z \leq 9\).
- Answer
- \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 127.2345\)
5. [T] \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\); \(S\) is the surface of sphere \(x^2 + y^2 + z^2 = 4\).
6. [T] \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + (z^2 - 1)\,\mathbf{\hat k}\); \(S\) is the surface of the solid bounded by cylinder \( x^2 + y^2 = 4\) and planes \(z = 0\) and \(z = 1\).
- Answer
- \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = 37.699\)
7. [T] \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + y^2 \,\mathbf{\hat j} + z^2 \,\mathbf{\hat k}\); \(S\) is the surface bounded above by sphere \(\rho = 2\) and below by cone \(\varphi = \dfrac{\pi}{4}\) in spherical coordinates. (Think of \(S\) as the surface of an “ice cream cone.”)
8. [T] \(\vecs F(x,y,z) = x^3\,\mathbf{\hat i} + y^3 \,\mathbf{\hat j} + 3a^2z \,\mathbf{\hat k} \, (constant \, a > 0)\); \(S\) is the surface bounded by cylinder \(x^2 + y^2 = a^2\) and planes \(z = 0\) and \(z = 1\).
- Answer
- \(\displaystyle \int_S \vecs F \cdot \vecs n \, ds = \dfrac{9\pi a^4}{2}\)
9. [T] Surface integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(S\) is the solid bounded by paraboloid \(z = x^2 + y^2\) and plane \(z = 4\), and \(\vecs F(x,y,z) = (x + y^2z^2)\,\mathbf{\hat i} + (y + z^2x^2)\,\mathbf{\hat j} + (z + x^2y^2) \,\mathbf{\hat k}\)
10. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = (e^{y^2} \,\mathbf{\hat i} + (y + \sin (z^2))\,\mathbf{\hat j} + (z - 1)\,\mathbf{\hat k}\) and \(S\) is upper hemisphere \(x^2 + y^2 + z^2 = 1, \, z \geq 0\), oriented upward.
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{\pi}{3}\)
11. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2z\,\mathbf{\hat k}\) and \(S\) is the surface bounded by cylinder \(x^2 + y^2 = 1\) and planes \(z = x + 2\) and \(z = 0\).
12. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\), when \(\vecs F(x,y,z) = x^2z^3 \,\mathbf{\hat i} + 2xyz^3\,\mathbf{\hat j} + xz^4 \,\mathbf{\hat k}\) and \(S\) is the surface of the box with vertices \((\pm 1, \, \pm 2, \, \pm 3)\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 0\)
13. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\), when \(\vecs F(x,y,z) = z \, \tan^{-1} (y^2)\,\mathbf{\hat i} + z^3 \ln(x^2 + 1) \,\mathbf{\hat j} + z\,\mathbf{\hat k}\) and \(S\) is a part of paraboloid \(x^2 + y^2 + z = 2\) that lies above plane \(z = 1\) and is oriented upward.
14. [T] Use a CAS and the divergence theorem to calculate flux \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = (x^3 + y^3)\,\mathbf{\hat i} + (y^3 + z^3)\,\mathbf{\hat j} + (z^3 + x^3)\,\mathbf{\hat k} \) and \(S\) is a sphere with center \((0, 0)\) and radius \(2.\)
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 241.2743\)
15. Use the divergence theorem to compute the value of flux integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = (y^3 + 3x)\,\mathbf{\hat i} + (xz + y)\,\mathbf{\hat j} + \left(z + x^4 \cos (x^2y)\right)\,\mathbf{\hat k}\) and \(S\) is the area of the region bounded by \(x^2 + y^2 = 1, \, x \geq 0, \, y \geq 0\), and \(0 \leq z \leq 1\).
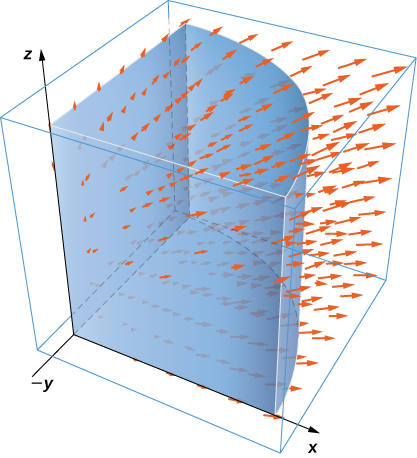
16. Use the divergence theorem to compute flux integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = y\,\mathbf{\hat j} - z\,\mathbf{\hat k}\) and \(S\) consists of the union of paraboloid \(y = x^2 + z^2, \, 0 \leq y \leq 1\), and disk \(x^2 + z^2 \leq 1, \, y = 1\), oriented outward. What is the flux through just the paraboloid?
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = -\pi\)
17. Use the divergence theorem to compute flux integral \(\displaystyle \iint_S \vecs F \cdot dS\), where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z^4 \,\mathbf{\hat k}\) and \(S\) is a part of cone \(z = \sqrt{x^2 + y^2}\) beneath top plane \(z = 1\) oriented downward.
18. Use the divergence theorem to calculate surface integral \(\displaystyle \iint_S \vecs F \cdot dS\) for \(\vecs F(x,y,z) = x^4\,\mathbf{\hat i} - x^3z^2\,\mathbf{\hat j} + 4xy^2 z\,\mathbf{\hat k}\), where \(S\) is the surface bounded by cylinder \(x^2 + y^2 = 1\) and planes \(z = x + 2\) and \(z = 0\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{2\pi}{3}\)
19. Consider \(\vecs F(x,y,z) = x^2\,\mathbf{\hat i} + xy\,\mathbf{\hat j} + (z + 1)\,\mathbf{\hat k}\). Let \(E\) be the solid enclosed by paraboloid \(z = 4 - x^2 - y^2\) and plane \(z = 0\) with normal vectors pointing outside \(E.\) Compute flux \(\vecs F\) across the boundary of \(E\) using the divergence theorem.
In exercises 20 - 23, use a CAS along with the divergence theorem to compute the net outward flux for the fields across the given surfaces \(S\).
20. [T] \(\vecs F = \langle x,\, -2y, \, 3z \rangle; \) \(S\) is sphere \(\{(x,y,z) : x^2 + y^2 + z^2 = 6 \}\).
- Answer
- \(15\sqrt{6}\pi\)
21. [T] \(\vecs F = \langle x, \, 2y, \, z \rangle\); \(S\) is the boundary of the tetrahedron in the first octant formed by plane \(x + y + z = 1\).
22. [T] \(\vecs F = \langle y - 2x, \, x^3 - y, \, y^2 - z \rangle\); \(S\) is sphere \(\{(x,y,z) \,:\, x^2 + y^2 + z^2 = 4\}.\)
- Answer
- \(-\dfrac{128}{3} \pi\)
23. [T] \(\vecs F = \langle x,y,z \rangle\); \(S\) is the surface of paraboloid \(z = 4 - x^2 - y^2\), for \(z \geq 0\), plus its base in the \(xy\)-plane.
For exercises 24 - 26, use a CAS and the divergence theorem to compute the net outward flux for the vector fields across the boundary of the given regions \(D\).
24. [T] \(\vecs F = \langle z - x, \, x - y, \, 2y - z \rangle\); \(D\) is the region between spheres of radius 2 and 4 centered at the origin.
- Answer
- \(-703.7168\)
25. [T] \(\vecs F = \dfrac{\vecs r}{\|\vecs r\|} = \dfrac{\langle x,y,z\rangle}{\sqrt{x^2+y^2+z^2}}\); \(D\) is the region between spheres of radius 1 and 2 centered at the origin.
26. [T] \(\vecs F = \langle x^2, \, -y^2, \, z^2 \rangle\); \(D\) is the region in the first octant between planes \(z = 4 - x - y\) and \(z = 2 - x - y\).
- Answer
- \(20\)
27. Let \(\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3xy\,\mathbf{\hat j} + xz^2\,\mathbf{\hat k}\). Use the divergence theorem to calculate \(\displaystyle \iint_S \vecs F \cdot dS\), where \(S\) is the surface of the cube with corners at \((0,0,0), \, (1,0,0), \, (0,1,0), \, (1,1,0), \, (0,0,1), \, (1,0,1), \, (0,1,1)\), and \((1,1,1)\), oriented outward.
28. Use the divergence theorem to find the outward flux of field \(\vecs F(x,y,z) = (x^3 - 3y)\,\mathbf{\hat i} + (2yz + 1)\,\mathbf{\hat j} + xyz\,\mathbf{\hat k}\) through the cube bounded by planes \(x = \pm 1, \, y = \pm 1, \) and \(z = \pm 1\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 8\)
29. Let \(\vecs F(x,y,z) = 2x\,\mathbf{\hat i} - 3y\,\mathbf{\hat j} + 5z\,\mathbf{\hat k}\) and let \(S\) be hemisphere \(z = \sqrt{9 - x^2 - y^2}\) together with disk \(x^2 + y^2 \leq 9\) in the \(xy\)-plane. Use the divergence theorem.
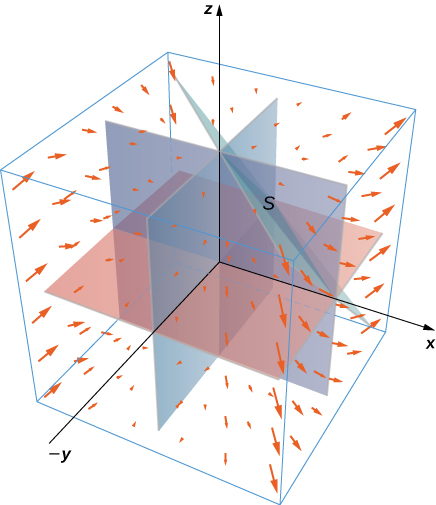
30. Evaluate \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS\), where \(\vecs F(x,y,z) = x^2 \,\mathbf{\hat i} + xy\,\mathbf{\hat j} + x^3y^3\,\mathbf{\hat k}\) and \(S\) is the surface consisting of all faces except the tetrahedron bounded by plane \(x + y + z = 1\) and the coordinate planes, with outward unit normal vector \(\vecs N.\)
- Answer
- \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS = \dfrac{1}{8}\)
31. Find the net outward flux of field \(\vecs F = \langle bz - cy, \, cx - az, \, ay - bx \rangle\) across any smooth closed surface in \(R^3\) where \(a, \, b,\) and \(c\) are constants.
32. Use the divergence theorem to evaluate \(\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds,\) where \(\vecs R(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) and \(S\) is sphere \(x^2 + y^2 + z^2 = a^2\), with constant \(a > 0\).
- Answer
- \(\displaystyle \iint_S ||\vecs R||\vecs R \cdot \vecs n \, ds = 4\pi a^4\)
33. Use the divergence theorem to evaluate \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = y^2 z\,\mathbf{\hat i} + y^3\,\mathbf{\hat j} + xz\,\mathbf{\hat k}\) and \(S\) is the boundary of the cube defined by \(-1 \leq x \leq 1, \, -1 \leq y \leq 1\), and \(0 \leq z \leq 2\).
34. Let \(R\) be the region defined by \(x^2 + y^2 + z^2 \leq 1\). Use the divergence theorem to find \(\displaystyle \iiint_R z^2 \, dV.\)
- Answer
- \(\displaystyle \iiint_R z^2 dV = \dfrac{4\pi}{15}\)
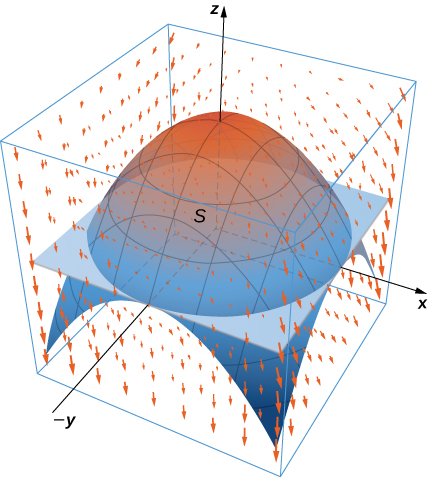
35. Let \(E\) be the solid bounded by the \(xy\)-plane and paraboloid \(z = 4 - x^2 - y^2\) so that \(S\) is the surface of the paraboloid piece together with the disk in the \(xy\)-plane that forms its bottom. If \(\vecs F(x,y,z) = (xz \, \sin(yz) + x^3) \,\mathbf{\hat i} + \cos (yz) \,\mathbf{\hat j} + (3zy^2 - e^{x^2+y^2})\,\mathbf{\hat k}\), find \(\displaystyle \iint_S \vecs F \cdot dS\) using the divergence theorem.
36. Let \(E\) be the solid unit cube with diagonally opposite corners at the origin and \((1, 1, 1),\) and faces parallel to the coordinate planes. Let \(S\) be the surface of \(E,\) oriented with the outward-pointing normal. Use a CAS to find \(\displaystyle \iint_S \vecs F \cdot dS\) using the divergence theorem if \(\vecs F(x,y,z) = 2xy\,\mathbf{\hat i} + 3ye^z\,\mathbf{\hat j} + x \sin z\,\mathbf{\hat k}\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 6.5759\)
37. Use the divergence theorem to calculate the flux of \(\vecs F(x,y,z) = x^3\,\mathbf{\hat i} + y^3\,\mathbf{\hat j} + z^3\,\mathbf{\hat k}\) through sphere \(x^2 + y^2 + z^2 = 1\).
38. Find \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) and \(S\) is the outwardly oriented surface obtained by removing cube \([1,2] \times [1,2] \times [1,2]\) from cube \([0,2] \times [0,2] \times [0,2]\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 21\)
39. Consider radial vector field \(\vecs F = \dfrac{\vecs r}{\|\vecs r\|} = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{1/2}}\). Compute the surface integral, where \(S\) is the surface of a sphere of radius a centered at the origin.
40. Compute the flux of water through parabolic cylinder \(S \,:\, y = x^2\), from \(0 \leq x \leq 2, \, 0 \leq z \leq 3\), if the velocity vector is \(\vecs F(x,y,z) = 3z^2\,\mathbf{\hat i} + 6\,\mathbf{\hat j} + 6xz\,\mathbf{\hat k}\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = 72\)
41. [T] Use a CAS to find the flux of vector field \(\vecs F(x,y,z) = z\,\mathbf{\hat i} + z\,\mathbf{\hat j} + \sqrt{x^2 + y^2}\,\mathbf{\hat k}\) across the portion of hyperboloid \(x^2 + y^2 = z^2 + 1\) between planes \(z = 0\) and \(z = \dfrac{\sqrt{3}}{3}\), oriented so the unit normal vector points away from the \(z\)-axis.
42. Use a CAS to find the flux of vector field \(\vecs F(x,y,z) = (e^y + x)\,\mathbf{\hat i} + (3 \, \cos (xz) - y)\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) through surface \(S,\) where \(S\) is given by \(z^2 = 4x^2 + 4y^2\) from \(0 \leq z \leq 4\), oriented so the unit normal vector points downward.
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = -33.5103\)
43. [T] Use a CAS to compute \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + 2z\,\mathbf{\hat k}\) and \(S\) is a part of sphere \(x^2 + y^2 + z^2 = 2\) with \(0 \leq z \leq 1\).
44. Evaluate \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = bxy^2\,\mathbf{\hat i} + bx^2y\,\mathbf{\hat j} + (x^2 + y^2)z^2 \,\mathbf{\hat k}\) and \(S\) is a closed surface bounding the region and consisting of solid cylinder \(x^2 + y^2 \leq a^2\) and \(0 \leq z \leq b\).
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = \pi a^4 b^2\)
45. [T] Use a CAS to calculate the flux of \(\vecs F(x,y,z) = (x^3 + y \, \sin z)\,\mathbf{\hat i} + (y^3 + z \, \sin x)\,\mathbf{\hat j} + 3z\,\mathbf{\hat k}\) across surface \(S,\) where \(S\) is the boundary of the solid bounded by hemispheres \(z = \sqrt{4 - x^2 - y^2}\) and \(z = \sqrt{1 - x^2 - y^2}\), and plane \(z = 0\).
46. Use the divergence theorem to evaluate \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = xy\,\mathbf{\hat i} - \dfrac{1}{2}y^2\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) and \(S\) is the surface consisting of three pieces: \(z = 4 - 3x^2 - 3y^2, \, 1 \leq z \leq 4\) on the top; \(x^2 + y^2 = 1, \, 0 \leq z \leq 1\) on the sides; and \(z = 0\) on the bottom.
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{5}{2}\pi\)
47. [T] Use a CAS and the divergence theorem to evaluate \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = (2x + y \, \cos z)\,\mathbf{\hat i} + (x^2 - y)\,\mathbf{\hat j} + y^2 z\,\mathbf{\hat k}\) and \(S\) is sphere \(x^2 + y^2 + z^2 = 4\) orientated outward.
48. Use the divergence theorem to evaluate \(\displaystyle \iint_S \vecs F \cdot dS,\) where \(\vecs F(x,y,z) = x\,\mathbf{\hat i} + y\,\mathbf{\hat j} + z\,\mathbf{\hat k}\) and \(S\) is the boundary of the solid enclosed by paraboloid \(y = x^2 + z^2 - 2\), cylinder \(x^2 + z^2 = 1\), and plane \(x + y = 2\), and \(S\) is oriented outward.
- Answer
- \(\displaystyle \iint_S \vecs F \cdot dS = \dfrac{21\pi}{2}\)
For the following exercises, Fourier’s law of heat transfer states that the heat flow vector \(\vecs F\) at a point is proportional to the negative gradient of the temperature; that is, \(\vecs F = - k \vecs \nabla T\), which means that heat energy flows hot regions to cold regions. The constant \(k > 0\) is called the conductivity, which has metric units of joules per meter per second-kelvin or watts per meter-kelvin. A temperature function for region \(D\) s given. Use the divergence theorem to find net outward heat flux \(\displaystyle \iint_S \vecs F \cdot \vecs n \, dS = -k \iint_S \vecs \nabla T \cdot N \, dS\) across the boundary \(S\) of \(D,\) where \(k = 1\).
49. \(T(x,y,z) = 100 + x + 2y + z\);
\(D = \{(x,y,z) : 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 \}\)
50. \(T(x,y,z) = 100 + e^{-z}\);
\(D = \{(x,y,z) : 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1 \}\)
- Answer
- \(- (1 - e^{-1})\)
51. \(T(x,y,z) = 100 e^{-x^2-y^2-z^2}\); \(D\) is the sphere of radius \(a\) centered at the origin.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


