16.R: Chapter 16 Review Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
True or False? Justify your answer with a proof or a counterexample.
1. The vector field
- Answer
- False
2. For vector field
3. The divergence of a vector field is a vector field.
- Answer
- False
4. If
Draw the following vector fields.
5.
- Answer
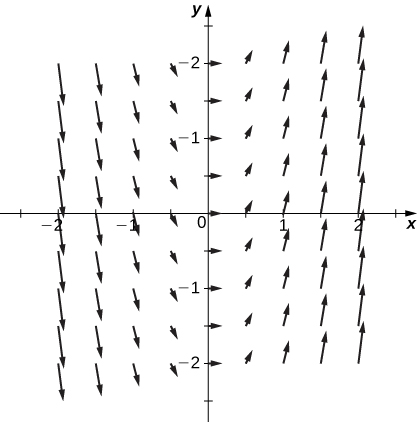
6.
Are the following the vector fields conservative? If so, find the potential function
7.
- Answer
- Conservative,
8.
9.
- Answer
- Conservative,
10.
Evaluate the following integrals.
11.
- Answer
12.
13.
- Answer
Find the divergence and curl for the following vector fields.
14.
15.
- Answer
- Divergence:
Curl:
Use Green’s theorem to evaluate the following integrals.
16.
17.
- Answer
Use Stokes’ theorem to evaluate
18.
19.
- Answer
Use the divergence theorem to evaluate
20.
21.
- Answer
22. Find the amount of work performed by a 50-kg woman ascending a helical staircase with radius 2 m and height 100 m. The woman completes five revolutions during the climb.
23. Find the total mass of a thin wire in the shape of a semicircle with radius
- Answer
24. Find the total mass of a thin sheet in the shape of a hemisphere with radius
25. Use the divergence theorem to compute the value of the flux integral over the unit sphere with
- Answer
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


