10.1: Introduction to Cartesian Coordinates in Space
( \newcommand{\kernel}{\mathrm{null}\,}\)
Up to this point in this text we have considered mathematics in a 2--dimensional world. We have plotted graphs on the
While there is wonderful mathematics to explore in "2D,'' we live in a "3D'' world and eventually we will want to apply mathematics involving this third dimension. In this section we introduce Cartesian coordinates in space and explore basic surfaces. This will lay a foundation for much of what we do in the remainder of the text.
Each point
Visualizing points in space on paper can be problematic, as we are trying to represent a 3-dimensional concept on a 2--dimensional medium. We cannot draw three lines representing the three axes in which each line is perpendicular to the other two. Despite this issue, standard conventions exist for plotting shapes in space that we will discuss that are more than adequate.
One convention is that the axes must conform to the right hand rule. This rule states that when the index finger of the right hand is extended in the direction of the positive
In Figure
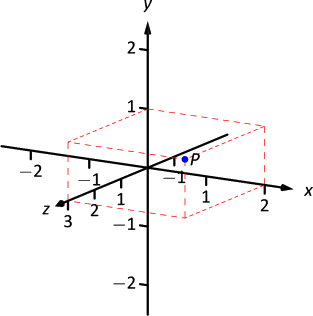
One can also consider the
Note
As long as the coordinate axes are positioned so that they follow the right hand rule, it does not matter how the axes are drawn on paper.
Measuring Distances
It is of critical importance to know how to measure distances between points in space. The formula for doing so is based on measuring distance in the plane, and is known (in both contexts) as the Euclidean measure of distance.
Definition 48: distance in space
Let
We refer to the line segment that connects points
Example
Let
Solution
The points
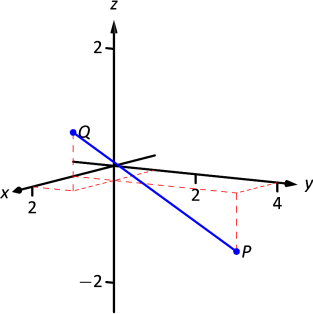
One cannot actually measure this line on the page and deduce anything meaningful; its true length must be measured analytically. Applying Definition 48, we have
Spheres
Just as a circle is the set of all points in the plane equidistant from a given point (its center), a sphere is the set of all points in space that are equidistant from a given point. Definition 48 allows us to write an equation of the sphere. We start with a point
Squaring both sides, we get the standard equation of a sphere in space with center at
KEY IDEA 45: STANDARD EQUATION OF A SPHERE IN SPACE
The standard equation of the sphere with radius
Example
Find the center and radius of the sphere defined by
Solution
To determine the center and radius, we must put the equation in standard form. This requires us to complete the square (three times).
The sphere is centered at
The equation of a sphere is an example of an implicit function defining a surface in space. In the case of a sphere, the variables
Introduction to Planes in Space
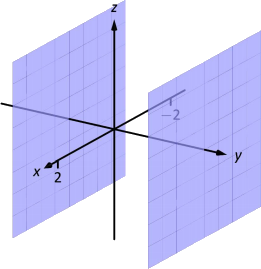
The coordinate axes naturally define three planes (shown in Figure
The equation
Example
Sketch the region defined by the inequalities
Solution
The region is all points between the planes
Cylinders
The equation
This surface looks like a "tube,'' or a "cylinder''; mathematicians call this surface a cylinder for an entirely different reason.
Definition 49: CYLINDER, Directrix and Rulings
Let
In this text, we consider curves
In the example preceding the definition, the curve
Example
Graph the cylinder following cylinders.
Solution
- We can view the equation
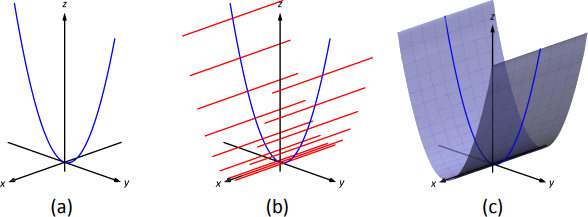
- We can view the equation
Surfaces of Revolution
One of the applications of integration we learned previously was to find the volume of solids of revolution -- solids formed by revolving a curve about a horizontal or vertical axis. We now consider how to find the equation of the surface of such a solid.
Consider the surface formed by revolving
We generalize the above principles to give the equations of surfaces formed by revolving curves about the coordinate axes.
KEY IDEA 46: SURFACES OF REVOLUTION, PART 1
Let
- The equation of the surface formed by revolving
- The equation of the surface formed by revolving
- The equation of the surface formed by revolving
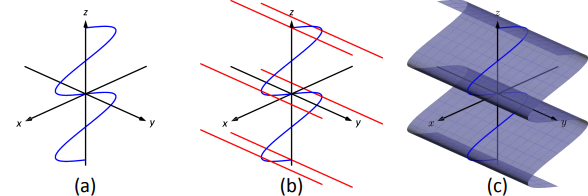
Example
Let
Solution
Using Key Idea 46, we find the surface has equation
Note how the surface (and hence the resulting equation) is the same if we began with the curve
This particular method of creating surfaces of revolution is limited. For instance, in Section 7.3 we found the volume of the solid formed by revolving
What we desire is a way of writing the surface of revolution formed by rotating
A value of
KEY IDEA 47: SURFACES OF REVOLUTION, PART 2
Let
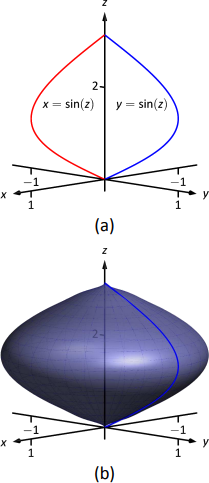
Example
Find the equation of the surface found by revolving
Solution
Using Key Idea 47, the surface has equation
Quadric Surfaces
Spheres, planes and cylinders are important surfaces to understand. We now consider one last type of surface, a quadric surface. The definition may look intimidating, but we will show how to analyze these surfaces in an illuminating way.
Definition 50: QUADRIC SURFACE
A quadric surface is the graph of the general second--degree equation in three variables:
When the coefficients
We study each shape by considering traces, that is, intersections of each surface with a plane parallel to a coordinate plane. For instance, consider the elliptic paraboloid
Divide both sides by
This describes an ellipse -- so cross sections parallel to the
Now consider cross sections parallel to the
Thus we see where the elliptic paraboloid gets its name: some cross sections are ellipses, and others are parabolas.
Such an analysis can be made with each of the quadric surfaces. We give a sample equation of each, provide a sketch with representative traces, and describe these traces.
Elliptic Paraboloid,
One variable in the equation of the elliptic paraboloid will be raised to the first power; above, this is the
Multiplying the right hand side by
Elliptic Cone,
One can rewrite the equation as
Ellipsoid,
If
Hyperboloid of One Sheet,
The one variable with a negative coefficient corresponds to the axis that the hyperboloid "opens'' along.
Hyperboloid of Two Sheets,
The one variable with a positive coefficient corresponds to the axis that the hyperboloid "opens'' along. In the case illustrated, when
Hyperbolic Paraboloid,
The parabolic traces will open along the axis of the one variable that is raised to the first power.
Example
Sketch the quadric surface defined by the given equation.
Solution
We first identify the quadric by pattern--matching with the equations given previously. Only two surfaces have equations where one variable is raised to the first power, the elliptic paraboloid and the hyperbolic paraboloid. In the latter case, the other variables have different signs, so we conclude that this describes a hyperbolic paraboloid. As the variable with the first power is
To make a decent sketch by hand, we need only draw a few traces. In this case, the traces
Graphing each trace in the respective plane creates a sketch as shown in Figure
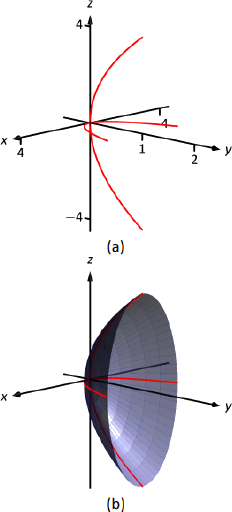
Figure
This is an ellipsoid. We can get a good idea of its shape by drawing the traces in the coordinate planes.
Graphing each trace in the respective plane creates a sketch as shown in Figure Figure
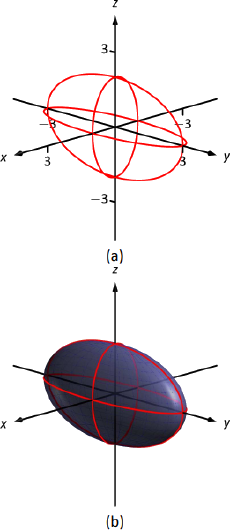
Figure
This defines a hyperbolic paraboloid, very similar to the one shown in the gallery of quadric sections. Consider the traces in the
Sketching these two parabolas gives a sketch like that in Figure Figure
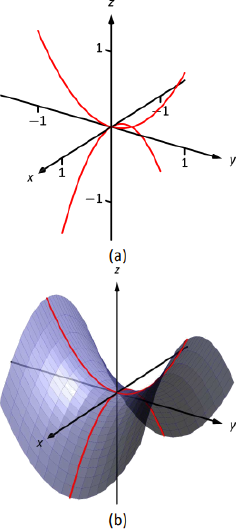
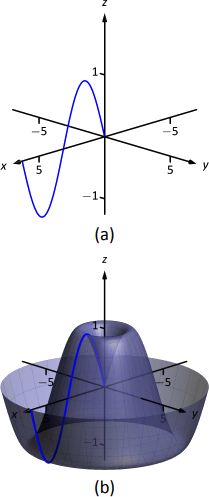
Example
Consider the quadric surface shown in Figure Figure
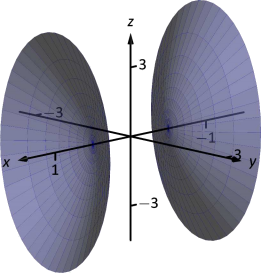
Solution
The image clearly displays a hyperboloid of two sheets. The gallery informs us that the equation will have a form similar to
We can immediately eliminate option (a), as the constant in that equation is not 1.
The hyperboloid "opens'' along the
The hyperboloid is wider in the
We already established that this equation describes a hyperboloid of two sheets that opens in the
We conclude that
This section has introduced points in space and shown how equations can describe surfaces. The next sections explore vectors, an important mathematical object that we'll use to explore curves in space.
Contributors and Attributions
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/


