9.5: Exercises

9.1. Growth of a cell. Consider the growth of a cell, assumed spherical in shape. Suppose that the radius of the cell increases at a constant rate \(k>0\) per unit time.

(a) At what rate would the volume, \(V\), increase ?

(b) At what rate would the surface area, \(S\), increase ?

(c) At what rate would the ratio of surface area to volume \(S / V\) change? Would this ratio increase or decrease as the cell grows?

Note: note that answers are expressed in terms of the radius of the cell.

9.2. Growth of a circular fungal colony. A fungal colony grows on a flat surface starting with a single spore. The shape of the colony edge is circular with the initial site of the spore at the centre of the circle. Suppose the radius of the colony increases at a constant rate \(C\) per unit time.

(a) At what rate does the area covered by the colony change ?

(b) The biomass of the colony is proportional to the area itoccupies. Let \(\alpha\) be the factor of proportionality. At what rate does the biomass increase?

9.3. Limb development. During early development, the limb of a fetus increases in size, but has constant proportions. Suppose that the limb is roughly a circular cylinder with radius \(r\) and length \(l\) in proportion

\[l / r=C \nonumber \]

where \(C\) is a positive constant. It is noted that during the initial phase of growth, the radius increases at an approximately constant rate, i.e. that

\[d r / d t=a . \nonumber \]

At what rate does the mass of the limb change during this time?

Note: assume that the density of the limb is \(1 \mathrm{gm} / \mathrm{cm}^{3}\) and recall that the volume of a cylinder is

\[V=A l \nonumber \]

where \(A\) is the base area (in this case of a circle) and \(l\) is length.

9.4. Pouring water in a trough. A rectangular trough is 2 meter long, \(0.5\) meter across the top and 1 meter deep. At what rate must water be poured into the trough such that the depth of the water is increasing at \(1 \mathrm{~m} / \mathrm{min}\) when the depth of the water is \(0.7 \mathrm{~m}\) ?

9.5. Spherical balloon. Gas is being pumped into a spherical balloon at the rate of \(3 \mathrm{~cm}^{3} / \mathrm{s}\).

(a) How fast is the radius increasing when the radius is \(15 \mathrm{~cm}\) ?

(b) Without using the result from (a), find the rate at which the surface area of the balloon is increasing when the radius is \(15 \mathrm{~cm}\).

9.6. Ice melting. A spherical piece of ice melts so that its surface area decreases at a rate of \(1 \mathrm{~cm}^{2} / \mathrm{min}\). Find the rate that the diameter decreases when the diameter is \(5 \mathrm{~cm}\).

9.7. Point moving on a parabola. A point moves along the parabola \(y=\) \(\frac{1}{4} x^{2}\) in such a way that at \(x=2\) the \(x\)-coordinate is increasing at the rate of \(5 \mathrm{~cm} / \mathrm{s}\). Find the rate of change of \(y\) at this instant.

9.8. Boyle’s Law. In chemistry, Boyle’s Law describes the behavior of an ideal gas: this law relates the volume \(V\) occupied by the gas to the temperature \(T\) and the pressure \(P\) as follows:

\[P V=n R T \nonumber \]

where \(n, R\) are positive constants.

(a) Suppose that pressure is kept fixed by allowing the gas to expand as the temperature is increased. Relate the rate of change of volume to the rate of change of temperature.

(b) Suppose that the temperature is held fixed and the pressure is decreased gradually. Relate the rate of change of the volume to the rate of change of pressure.

9.9. Spread of a population. In 1905 a Bohemian farmer accidentally allowed several muskrats to escape an enclosure. Their population grew and spread, occupying increasingly larger areas throughout Europe. In a classical paper in ecology, it was shown by the scientist Skellam (1951) that the square root of the occupied area increased at a constant rate, \(k\).

Determine the rate of change of the distance (from the site of release) that the muskrats had spread. Assume that the expanding area of occupation is circular.

9.10. A convex lens. A particular convex lens has a focal length of \(f=\) \(10 \mathrm{~cm}\). Let \(p\) be the distance between an object and the lens, and \(q\) the distance between its image and the lens. These distances are related to the focal length \(f\) by the equation:

\[\frac{1}{f}=\frac{1}{p}+\frac{1}{q} . \nonumber \]

Consider an object which is \(30 \mathrm{~cm}\) away from the lens and moving away at \(4 \mathrm{~cm} / \mathrm{sec}\).

How fast is its image moving and in which direction?

9.11. A conical cup. Water is leaking out of a small hole at the tip of a conical paper cup at the rate of \(1 \mathrm{~cm}^{3} / \mathrm{min}\). The cup has height \(8 \mathrm{~cm}\) and radius \(6 \mathrm{~cm}\), and is initially full up to the top.

Find the rate of change of the height of water in the cup when the cup just begins to leak.

Formula: Note that the volume of a cone is \(V=(\pi / 3) r^{2} h\).

9.12. Conical tank. Water is leaking out of the bottom of an inverted conical tank at the rate of \(\frac{1}{10} \mathrm{~m}^{3} / \mathrm{min}\), and at the same time is being pumped in the top at a constant rate of \(k \mathrm{~m}^{3} / \mathrm{min}\). The tank has height \(6 \mathrm{~m}\) and the radius at the top is \(2 \mathrm{~m}\).

Determine the constant \(k\) if the water level is rising at the rate of \(\frac{1}{5} \mathrm{~m} / \mathrm{min}\) when the height of the water is \(2 \mathrm{~m}\).

9.13. The gravel pile. Gravel is being dumped from a conveyor belt at the rate of \(30 \mathrm{ft}^{3} / \mathrm{min}\) in such a way that the gravel forms a conical pile whose base diameter and height are always equal.

How fast is the height of the pile increasing when the height is \(10 \mathrm{ft}\) ?

9.14. The sand pile. Sand is piled onto a conical pile at the rate of \(10 \mathrm{~m}^{3} / \mathrm{min}\). The sand keeps spilling to the base of the cone so that the shape always has the same proportions: that is, the height of the cone is equal to the radius of the base.

Find the rate at which the height of the sandpile increases when the height is \(5 \mathrm{~m}\).

9.15. Conical water reservoir. Water is flowing into a conical reservoir at a rate of \(4 \mathrm{~m}^{3} / \mathrm{min}\). The reservoir is \(3 \mathrm{~m}\) in radius and \(12 \mathrm{~m}\) deep.

(a) How fast is the radius of the water surface increasing when the depth of the water is \(8 \mathrm{~m}\) ?

(b) In (a), how fast is the surface rising?

9.16. Sliding ladder. A ladder 10 meters long leans against a vertical wall. The foot of the ladder starts to slide away from the wall at a rate of 3 \(\mathrm{m} / \mathrm{s}\).

(a) Find the rate at which the top of the ladder is moving downward when its foot is 8 meters away from the wall.

(b) In (a), find the rate of change of the slope of the ladder.

9.17. Sliding ladder. A ladder \(5 \mathrm{~m}\) long rests against a vertical wall. If the bottom of the ladder slides away from the wall at the rate of \(0.5 \mathrm{~m} / \mathrm{min}\) how fast is the top of the ladder sliding down the wall when the base of the ladder is \(1 \mathrm{~m}\) away from the wall?

9.18. Species diversity in an area. Ecologists are often interested in the relationship between the area of a region \((A)\) and the number of different species \(S\) that can inhabit that region. Hopkins (1955)suggested a relationship of the form [Hopkins, 1955]

\[S=a \ln (1+b A) \nonumber \]

where \(a\) and \(b\) are positive constants.

Find the rate of change of the number of species with respect to the area. Does this function have a maximum?

9.19. The burning candle. A candle is placed a distance \(l_{1}\) from a thin block of wood of height \(H\). The block is a distance \(l_{2}\) from a wall as shown in Figure 9.12. The candle burns down so that the height of the flame, \(h_{1}\) decreases at the rate of \(3 \mathrm{~cm} / \mathrm{hr}\). Find the rate at which the length of the shadow \(y\) cast by the block on the wall increases.

Note: your answer should be in terms of the constants \(l_{1}\) and \(l_{2}\). This is a challenging problem.

Figure 9.12: Figure for Exercise 19; shadow cast by burning candle.

9.20. Implicit differentiation. Use implicit differentiation to show that the derivative of the function

\[y=x^{1 / 3} \nonumber \]

is

\[y^{\prime}=(1 / 3) x^{-2 / 3} . \nonumber \]

First write the relationship in the form \(y^{3}=x\), and then find \(d y / d x\).

9.21. Generalizing the Power Law.

(a) Use implicit differentiation to calculate the derivative of the function

\[y=f(x)=x^{n / m} \nonumber \]

where \(m\) and \(n\) are integers (hint: rewrite the equation in the form \(y^{m}=x^{n}\) first).

(b) Use your result to derive the formulas for the derivatives of the functions \(y=\sqrt{x}\) and \(y=x^{-1 / 3}\).

9.22. Tangent lines to a circle.

The equation of a circle with radius \(r\) and centre at the origin is

\[x^{2}+y^{2}=r^{2} \nonumber \]

(a) Use implicit differentiation to find the slope of a tangent line to the circle at some point \((x, y)\).

(b) Use this result to find the equations of the tangent lines of the circle at the points whose \(x\) coordinate is \(x=r / \sqrt{3}\).

(c) Use the same result to show that the tangent line at any point on the circle is perpendicular to the radial line drawn from that point to the centre of the circle

Note: Two lines are perpendicular if their slopes are negative reciprocals.

9.23. Implicit differentiation. For each of the following, find the derivative of \(y\) with respect to \(x\).

(a) \(y^{6}+3 y-2 x-7 x^{3}=0\)

(b) \(e^{y}+2 x y=\sqrt{3}\)

9.24. Tangent line to a circle. The equation of a circle with radius 5 and centre at \((1,1)\) is

\[(x-1)^{2}+(y-1)^{2}=25 \nonumber \]

(a) Find the slope of the tangent line to this curve at the point \((4,5)\).

(b) Find the equation of the tangent line.

9.25. Tangent to a hyperbola. The curve

\[x^{2}-y^{2}=1 \nonumber \]

is a hyperbola. Use implicit differentiation to show that for large \(x\) and \(y\) values, the slope \(d y / d x\) of the curve is approximately 1.

9.26. An ellipse.

Use implicit differentiation to find the points on the ellipse

\[\frac{x^{2}}{4}+\frac{y^{2}}{9}=1 \nonumber \]

at which the slope is \(-1 / 2\).

9.27. Motion of a cell.

In the study of cell motility, biologists often investigate a type of cell called a keratocyte, an epidermal cell that is found in the scales of fish. This flat, elliptical cell crawls on a flat surface, and is known to be important in healing wounds. The \(2 \mathrm{D}\) outline of the cell can be approximated by the ellipse

\[x^{2} / 100+y^{2} / 25=1 \nonumber \]

where \(x\) and \(y\) are distances in \(\mu \mathrm{m}\). When the motion of the cell is filmed, points on the "leading edge" (top arc of the ellipse) move in a direction perpendicular to the edge.

Determine the direction of motion of the point \(\left(x_{p}, y_{p}\right)\) on the leading edge, i.e. find the slope of the dark arrow in Figure 9.13.

Figure 9.13: An elliptical cell

Units.

Note that \(1 \mu \mathrm{m}\), often called "1 micron", is \(10^{-6}\) meters.

9.28. The Folium of Descartes. A famous curve (see Figure 9.14) that was studied historically by many mathematicians (including Descartes) is

\[x^{3}+y^{3}=3 a x y \nonumber \]

Assume that \(a\) is a positive constant.

Figure 9.14: The Folium of Descartes in Exercise 9.28

(a) Explain why this curve cannot be described by a function such as \(y=f(x)\) over the domain \(-\infty<x<\infty\).

(b) Use implicit differentiation to find the slope of this curve at a point \((x, y)\).

(c) Determine whether the curve has a horizontal tangent line anywhere, and if so, find the \(x\) coordinate of the points at which this occurs.

(d) Does implicit differentiation allow you to find the slope of this curve at the point \((0,0)\) ?

9.29. Isotherms in the Van-der Waal’s equation. In thermodynamics, the Van der Waal’s equation relates the mean pressure, \(p\) of a substance to its molar volume \(v\) at some temperature \(T\) as follows:

\[\left(p+\frac{a}{v^{2}}\right)(v-b)=R T, \nonumber \]

where \(a, b, R\) are constants. Chemists are interested in the curves described by this equation when the temperature is held fixed.

Note: these curves are called isotherms.

(a) Find the slope, \(d p / d v\), of the isotherms at a given point \((v, p)\).

(b) Determine where points occur on the isotherms at which the slope is horizontal.

9.30. The circle and parabola: A circle of radius 1 is made to fit inside the parabola \(y=x^{2}\) as shown in figure 9.15. Find the coordinates of the centre of this circle, i.e. find the value of the unknown constant \(c\) (hint: set up conditions on the points of intersection of the circle and the parabola which are labeled \((a, b)\) in the figure. What must be true about the tangent lines at these points?).

Figure 9.15: Figure for Exercise 30; circle inside a parabola.

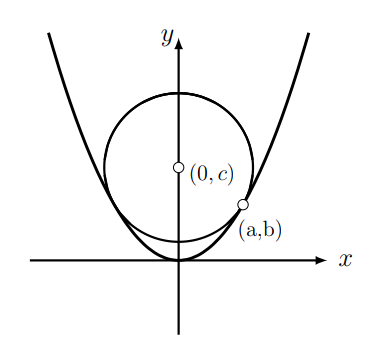
9.31. Equation of a tangent line. Consider the curve whose equation is

\[x^{3}+y^{3}+2 x y=4, y=1 \text { when } x=1 . \nonumber \]

(a) Find the equation of the tangent line to the curve when \(x=1\).

(b) Find \(y^{\prime \prime}\) at \(x=1\).

(c) Is the graph of \(y=f(x)\) concave up or concave down near \(x=1\) ? (hint: differentiate the equation \(x^{3}+y^{3}+2 x y=4\) twice with respect to \(x\) ).