16.1: Exercises

16.1. Multiple choice.

(1) The equation of the tangent line to the function \(y=f(x)\) at the point \(x_{0}\) is

(a) \(y=f^{\prime}\left(x_{0}\right)+f\left(x_{0}\right)\left(x-x_{0}\right)\)

(b) \(y=x_{0}+f\left(x_{0}\right) / f^{\prime}\left(x_{0}\right)\)

(c) \(y=f(x)-f^{\prime}(x)\left(x-x_{0}\right)\)

(d) \(y=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\)

(e) \(y=f\left(x_{0}\right)-f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\)

(2) The functions \(f(x)=x^{2}\) and \(g(x)=x^{3}\) are equal at \(x=0\) and at \(x=1\). Between \(x=0\) and at \(x=1\), for what value of \(x\) are their graphs furthest apart?

(a) \(x=1 / 2\)

(b) \(x=2 / 3\)

(c) \(x=1 / 3\)

(d) \(x=1 / 4\)

(e) \(x=3 / 4\)

(3) Consider a point in the first quadrant on the hyperbola \(x^{2}-y^{2}=1\) with \(x=2\). The slope of the tangent line at that point is

(a) \(2 / \sqrt{3}\)

(b) \(2 / \sqrt{5}\)

(c) \(1 / \sqrt{3}\)

(d) \(\sqrt{5} / 2\)

(e) \(2 / 3\)

(4) For \(a, b>0\), solving the equation \(\ln (x)=2 \ln (a)-3 \ln (b)\) for \(x\) leads to

(a) \(x=e^{2 a-3 b}\)

(b) \(x=2 a-3 b\)

(c) \(x=a^{2} / b^{3}\)

(d) \(x=a^{2} b^{3}\)

(e) \(x=(a / b)^{6}\)

(5) The function \(y=f(x)=\arctan (x)-(x / 2)\) has local maXima (LX), local minima (LM) and inflection points(IP) as follows:

(a) LX: \(x=1\), LM: \(x=-1\), IP: \(x=0\)

(b) LX: \(x=-1\), LM: \(x=1\), IP: \(x=0\)

(c) LX: \(x=-1\), LM: \(x=1\), IP: none

(d) LX: \(x=\sqrt{3}\), LM: \(x=-\sqrt{3}\), IP: \(x=0\)

(e) LX: \(x=-\sqrt{3}\), LM: \(x=\sqrt{3}\), IP: \(x=0\).

(6) Consider the function \(y=f(x)=3 e^{-2 x}-5 e^{-4 x}\).

(a) The function has a local maximum at \(x=(1 / 2) \ln (10 / 3)\)

(b) The function has a local minimum at \(x=(1 / 2) \ln (10 / 3)\)

(c) The function has a local maximum at \(x=(-1 / 2) \ln (3 / 5)\)

(d) The function has a local minimum at \(x=(1 / 2) \ln (3 / 5)\)

(e) The function has a local maximum at \(x=(-1 / 2) \ln (3 / 20)\)

(7) Let \(m_{1}\) be the slope of the function \(y=3^{x}\) at the point \(x=0\) and let \(m_{2}\) be the slope of the function \(y=\log _{3} x\) at \(x=1\) Then

(a) \(m_{1}=\ln (3) m_{2}\)

(b) \(m_{1}=m_{2}\)

(c) \(m_{1}=-m_{2}\)

(d) \(m_{1}=1 / m_{2}\)

(e) \(m_{1}=m_{2} / \ln (3)\)

(8) Consider the curve whose equation is \(x^{4}+y^{4}+3 x y=5\). The slope of the tangent line, \(d y / d x\), at the point \((1,1)\) is

(a) 1

(b) \(-1\)

(c) 0

(d) \(-4 / 7\)

(e) \(1 / 7\)

(9) Two kinds of bacteria are found in a sample of tainted food. It is found that the population size of type \(1, N_{1}\) and of type \(2, N_{2}\) satisfy the equations

\[\begin{array}{ll} \frac{d N_{1}}{d t}=-0.2 N_{1}, & N_{1}(0)=1000 \\ \frac{d N_{2}}{d t}=0.8 N_{2}, & N_{2}(0)=10 \end{array} \nonumber \]

Then the population sizes are equal \(N_{1}=N_{2}\) at the following time:

(a) \(t=\ln (40)\)

(b) \(t=\ln (60)\)

(c) \(t=\ln (80)\)

(d) \(t=\ln (90)\)

(e) \(t=\ln (100)\)

(10) In a conical pile of sand the ratio of the height to the base radius is always \(r / h=3\). If the volume is increasing at rate \(3 \mathrm{~m}^{3} / \mathrm{min}\), how fast (in \(\mathrm{m} / \mathrm{min}\) ) is the height changing when \(h=2 \mathrm{~m}\) ?

Note

Formula:

Note that the volume of a cone with height \(h\) and radius \(r\) is \(V=(\pi / 3) r^{2} h\).)

(a) \(1 /(12 \pi)\)

(b) \((1 / \pi)^{1 / 3}\)

(c) \(27 /(4 \pi)\)

(d) \(1 /(4 \pi)\)

(e) \(1 /(36 \pi)\)

(11) Shown in Figure \(16.1\) is a function and its tangent line at \(x=x_{0}\). The tangent line intersects the \(x\) axis at the point \(x=x_{1}\). Based on this figure, the coordinate of the point \(x_{1}\) is

Figure 16.1: Graph for Exercise 1; a function and its tangent line.

(a) \(x_{1}=x_{0}+\frac{f\left(x_{0}\right)}{f^{\prime}\left(x_{0}\right)}\)

(b) \(x_{1}=x_{0}-f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)\)

(c) \(x_{1}=x_{0}-\frac{f^{\prime}\left(x_{1}\right)}{f\left(x_{1}\right)}\)

(d) \(x_{1}=x_{0}+\frac{f^{\prime}\left(x_{1}\right)}{f\left(x_{1}\right)}\)

(e) \(x_{1}=x_{0}-\frac{f\left(x_{0}\right)}{f^{\prime}\left(x_{0}\right)}\)

(12) Consider Euler’s method. For the differential equation and initial condition

\[\frac{d y}{d t}=(2-y), \quad y(0)=1 \nonumber \]

using one time step of size \(\Delta t=0.1\) leads to which value of the solution at time \(t=0.1\) ?

(a) \(y(0.1)=2\)

(b) \(y(0.1)=2.1\)

(c) \(y(0.1)=2.2\)

(d) \(y(0.1)=1.2\)

(e) \(y(0.1)=1.1\)

(13) Consider the function \(y=\cos (x)\) and its tangent line to this function at the point \(x=\pi / 2\). Using that tangent line as a linear approximation of the function would lead to

(a) Overestimating the value of the actual function for any nearby \(x\).

(b) Underestimating the value of the actual function for any nearby \(x\).

(c) Overestimating the function when \(x>\pi / 2\) and underestimating the function when \(x<\pi / 2\).

(d) Overestimating the function when \(x<\pi / 2\) and underestimating the function when \(x>\pi / 2\).

(e) Overestimating the function when \(x<0\) and underestimating the function when \(x>0\).

16.2. Related Rates. Two spherical balloons are connected so that one inflates as the other deflates, the sum of their volumes remaining constant. When the first balloon has radius \(10 \mathrm{~cm}\) and its radius is increasing at \(3 \mathrm{~cm} / \mathrm{sec}\), the second balloon has radius \(20 \mathrm{~cm}\). What is the rate of change of the radius of the second balloon?

Note

Formula:

Note that the volume of a sphere of radius \(r\) is \(V=(4 / 3) \pi r^{3}\).

16.3. Particle velocity. A particle is moving along the \(x\) axis so that its distance from the origin at time \(t\) is given by

\[x(t)=(t+2)^{3}+\lambda t \nonumber \]

where \(\lambda\) is a constant

(a) Determine the velocity \(v(t)\) and the acceleration \(a(t)\).

(b) Determine the minimum velocity over all time.

16.4. Motion. A particle’s motion is described by \(y(t)=t^{3}-6 t^{2}+9 t\) where \(y(t)\) is the displacement (in metres) \(t\) is time (in seconds) and \(0 \leq t \leq 4\) seconds.

(a) During this time interval, when is the particle furthest from its initial position ?

(b) During this time interval, what is the greatest speed of the particle?

(c) What is the total distance (including both forward and backward directions) that the particle has travelled during this time interval?

16.5. Falling object. Consider an object thrown upwards with initial velocity \(v_{0}>0\) and initial height \(h_{0}>0\). Then the height of the object at time \(t\) is given by

\[y=f(t)=-\frac{1}{2} g t^{2}+v_{0} t+h_{0} \nonumber \]

Find critical points of \(f(t)\) and use both the second and first derivative tests to establish that this is a local maximum.

16.6. Linear approximation. Find a linear approximation to the function \(y=x^{2}\) at the point whose \(x\) coordinate is \(x=2\). Use your result to approximate the value of \((2.0001)^{2}\).

16.7. HIV virus. Initially, a patient has 1000 copies of the virus. How long does it take until the HIV infection is detectable? Assume that the number of virus particles \(y\) grows according to the equation

\[\frac{d y}{d t}=0.05 y \nonumber \]

where \(t\) is time in days, and that the smallest detectable viral load is 350,000 particles. Leave your answer in terms of logarithms.

16.8. Fish generations. In Fish River, the number of salmon (in thousands), \(x\), in a given year is linked to the number of salmon (in thousands), \(y\), in the following year by the function

\[y=A x e^{-b x} \nonumber \]

where \(A, b>0\) are constants.

(a) For what number of salmon is there no change in the number from one year to the next?

(b) Find the number of salmon that would yield the largest number of salmon in the following year.

16.9. Polynomial. Find a polynomial of third degree that has a local maximum a \(x=1\), a zero and an inflection point at \(x=0\), and goes through the point \((1,2)\) (hint: assume \(p(x)=a x^{3}+b x^{2}+c x+d\) and find the values of \(a, b, c, d)\).

16.10. Critical points.

(a) Find critical points for the function \(y=e^{x}(1-\ln (x))\) for \(0.1 \leq x \leq 2\) and classify their types.

(b) The function \(y=\ln (x)-e^{x}\) has a critical point in the interval \(0.1 \leq\) \(x \leq 2\). It is not possible to solve for the value of \(x\) at that point, but it is possible to find out what kind of critical point that is. Determine whether that point is a local maximum, minimum, or inflection point.

16.11. Lennard-Jones potential. The Lennard-Jones potential, \(V(x)\) is the potential energy associated with two uncharged molecules a distance \(x\) apart, and is given by the formula

\[V(x)=\frac{a}{x^{12}}-\frac{b}{x^{6}} \nonumber \]

where \(a, b>0\). Molecules would tend to adjust their separation distance so as to minimize this potential. Find any local maxima or minima of this potential. Find the distance between the molecules, \(x\), at which \(V(x)\) is minimized and use the second derivative test to verify that this is a local minimum.

16.12. Rectangle inscribed in a circle. Find the dimensions of the largest rectangle that can fit exactly into a circle whose radius is \(r\).

16.13. Race track. Figure \(16.2\) shows a \(1 \mathrm{~km}\) race track with circular ends. Find the values of \(x\) and \(y\) that maximize the area of the rectangle.

Figure 16.2: This shape is investigated in both Exercise 13 and 14; maximizing area or a racetrack, rate of growth of a leaf.

16.14. Leaf shape. Now suppose that Figure 16.2 shows the shape of a leaf of some plant. If the plant grows so that \(x\) increases at the rate \(2 \mathrm{~cm} /\) year and \(y\) increases at the rate \(1 \mathrm{~cm} /\) year, at what rate is the leaf’s entire area increasing?

16.15. Shape of E. coli. A cell of the bacterium E. coli has the shape of a cylinder with two hemispherical caps, as shown in Figure 16.3. Consider this shape, with \(h\) the height of the cylinder, and \(r\) the radius of the cylinder and hemispheres.

Figure 16.3: Shape of the cells described in Exercises 15 and 16

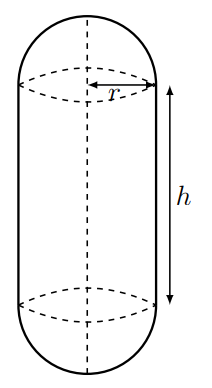
(a) Find the values of \(r\) and \(h\) that lead to the largest volume for a fixed constant surface area, \(S=\) constant.

(b) Describe or sketch the shape you found in (a).

(c) A typical E. coli cell has \(h=1 \mu \mathrm{m}\) and \(r=0.5 \mu \mathrm{m}\). Based on your results in (a) and (b), would you agree that E. coli has a shape that maximizes its volume for a fixed surface area? (Explain your answer).

16.16. Changing cell shape. If the cell shown in Figure \(16.3\) is growing so that the height increases twice as fast as the radius, and the radius is growing at \(1 \mu \mathrm{m}\) per day, at what rate does the volume of the cell increase? Leave your answer in terms of the height and radius of the cell.

16.17. Minima and Maxima.

Note

Formula.

Note that a hemisphere of radius \(r\) has volume \(V=(2 / 3) \pi r^{3}\) and surface area \(S=2 \pi r^{2}\).

For a cylinder: \(V=\pi r^{2} h\) and \(S=2 \pi r h\).

(a) Consider the polynomial \(y=4 x^{5}-15 x^{4}\). Find all local minima maxima, and inflection points for this function.

(b) Find the global minimum and maximum for this function on the interval \([-1,1]\)

16.18. Minima and Maxima. Consider the polynomial \(y=-x^{5}-x^{4}+3 x^{3}\). Use calculus to find all local minima maxima, and inflection points for this function.

16.19. Growth of vine. A vine grows up a tree in the form of a helix as shown on the left in Figure 16.4. If the length of the vine increases at a constant rate \(\alpha \mathrm{cm} /\) day, at what rate is the height of its growing tip increasing? Assume that the radius of the tree is \(r\) and the pitch of the helix (i.e. height increase for each complete turn of the helix) is \(p\), a positive constant. Note that the right panel in Figure \(16.4\) shows the unwrapped cylinder, with the vine’s location along it.

Figure 16.4: Growth of a vine in the shape of a spiral for Exercise 19.

16.20. Newton’s law of cooling. Newton’s Law of cooling leads to a differential equation that predicts the temperature \(T(t)\) of an object whose initial temperature is \(T_{0}\) in an environment whose temperature is \(E\). The predicted temperature is given by \(T(t)=E+\left(T_{0}-E\right) e^{-k t}\) where \(t\) is time and \(k\) is a constant. Shown in Figure \(16.5\) is some data points plotted as \(\ln (T(t)-E)\) versus time in minutes. The ambient temperature was \(E=22^{\circ} \mathrm{C}\). Also shown on the graph is the line that best fits those 11 points. Find the value of the constant \(k\).

Figure 16.5: Figure for Exercise 20; Newton’s law of cooling.

16.21. Blood alcohol. Blood alcohol level (BAL), the amount of alcohol in your blood stream (here represented by \(B(t)\), is measured in milligrams of alcohol per 10 millilitres of blood. At the end of a party (time \(t=0\) ), a drinker is found to have \(B(0)=0.08\) (the legal level for driving impairment), and after that time, \(B(t)\) satisfies the differential equation

\[\frac{d B}{d t}=-k B, \quad k>0 \nonumber \]

where \(k\) is a constant that represents the rate of removal of alcohol form the blood stream by the liver.

(a) If the drinker had waited for 3 hrs before driving (until = 3 ), his BAL would have dropped to \(0.04\). Determine the value of the rate constant \(k\) (specifying appropriate units) for this drinker.

(b) According to the model, how much longer would it take for the BAL to drop to \(0.01 ?\)

16.22. Population with immigration. An island has a bird population of density \(P(t)\). New birds arrive continually with a constant colonization rate \(C\) birds per day. Each bird also has a constant probability per day, \(\gamma\), of leaving the island. At time \(t=0\) the bird population is \(P(0)=P_{0}\)

(a) Write a differential equation that describes the rate of change of the bird population on the island.

(b) Find the steady state of that equation and interpret this in terms of the bird population.

(c) Give the solution of the differential equation you found in (b) and show that it satisfies the following two properties:

(i) the initial condition,

(ii) as \(t \rightarrow \infty\) it approaches the steady state you found in (b).

(d) If the island has no birds on it at time \(t=0\), how long would it take for the bird population to grow to \(80 \%\) of the steady state value?

16.23. Learning.

(a) It takes you \(1 \mathrm{hrs}\) (total) to travel to and from \(\mathrm{SFU}\) every day to study Philosophy 101 . The amount of new learning (in arbitrary units) that you can get by spending \(t\) hours at the university is given approximately by

\[L_{P}(t)=\frac{10 t}{9+t} \nonumber \]

How long should you stay at \(\mathrm{SFU}\) on a given day if you want to maximize your learning per time spent?

Note: time spent includes travel time.

(b) If you take Math 10000 instead of Philosophy, your learning at time \(t\) is

\[L_{M}(t)=t^{2} \nonumber \]

How long should you stay at SFU to maximize your learning in that case?

16.24. Learning and forgetting. Knowledge can be acquired by studying, but it is forgotten over time A simple model for learning represents the amount of knowledge, \(y(t)\), that a person has at time \(t\) (in years) by a differential equation

\[\frac{d y}{d t}=S-f y, \nonumber \]

where \(S \geq 0\) is the rate of studying and \(f \geq 0\) is the rate of forgetting. We assume that \(S\) and \(f\) are constants that are different for each person.

Note: your answers to the following questions will contain constants such as \(S\) or \(f\).

(a) Mary never forgets anything. What does this imply about the constants \(S\) and \(f\) ? Mary starts studying in school at time \(t=0\) with no knowledge at all. How much knowledge does she have after 4 years (i.e. at \(t=4\) )?

(b) Tom learned so much in preschool that his knowledge when entering school at time \(t=0\) is \(y=100\). However, once Tom is in school, he stops studying completely. What does this imply about the constants \(S\) and \(f\) ? How long does it take him to forget \(75 \%\) of what he knew?

(c) Jane studies at the rate of 10 units per year and forgets at rate of \(0.2\) per year. Sketch a "direction field" ("slope field") for the differential equation describing Jane’s knowledge. Add a few curves \(y(t)\) to show how Jane’s knowledge changes with time.

16.25. Least cost. A rectangular plot of land has dimensions \(L\) by \(D\) as depicted in Figure 16.6. A pipe is to be built joining points \(A\) and \(C\). The pipe can be above ground along the border of the plot (Section \(A B\) ), but has to be buried underground along the segment \(B C\). The cost per unit length of the underground portion is 3 times that of the cost of the above ground portion. Determine the distance \(y\) so that the cost of the pipe is as low as possible.

Figure 16.6: Figure for Exercise 25; least cost for installing a pipe.

16.26. Least heat loss. In an effort to increase sustainability, the university is aiming to use the shortest length of pipes to connect the buildings (labeled \(B\) ) with the steam power plant (labeled \(P\) ) in Figure \(16.7\) in order reduce loss of heat from the pipes to the surroundings.

Figure 16.7: Figure for Exercise 26; least heat loss.

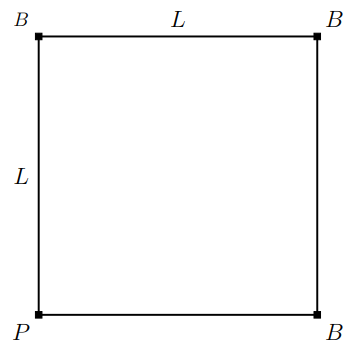
(a) Set up a model and describe how you would solve this problem. Assume that the four sites are located at the corners of a square of side length \(L\).

(b) How long is the shortest total pipe length connecting \(P\) to the 3 other corners?

16.27. Logistic equation and its solution.

(a) Show that the function

\[y(t)=\frac{1}{1+e^{-t}} \nonumber \]

satisfies the differential equation

\[\frac{d y}{d t}=y(1-y) . \nonumber \]

(b) What is the initial value of \(y\) at \(t=0\) ?

(c) For what value of \(y\) is the growth rate largest?

(d) What happens to \(y\) after a very long time?

16.28. Human growth. Given a population of 6 billion people on Planet Earth, and using the approximate growth rate of \(r=0.0125\) per year, how long ago was this population only 1 million? Assume that the growth has been the same throughout history (which is not actually true).

16.29. Ducks in a row. Graduate student Ryan Lukeman studies behavior of duck flocks swimming near Canada Place in Vancouver, BC. This figure from his \(\mathrm{PhD}\) thesis shows his photography set-up. Here \(H=10\) meters is the height from sea level up to his camera aperture at the observation point, \(D=2\) meters is the width of a pier (a stationary platform whose size is fixed), and \(x\) is the distance from the pier to the leading duck in the flock (in meters). A visual angle subtended at the camera is shown as \(\alpha\).

Figure 16.8: Figure for Exercise 29; ducks in a row.

If the visual angle is increasing at the rate of \(1 / 100\) radians per second, at what rate is the distance \(x\) changing at the instant that \(x=3\) meters?

16.30. Circular race track. Two runners are running around a circular race track whose length is \(400 \mathrm{~m}\), as shown in Figure 16.9(a). The first runner makes a full revolution every \(100 \mathrm{~s}\) and the second runner every \(150 \mathrm{~s}\). They start at the same time at the start position, and the angles subtended by each runner with the radius of the start position are \(\theta_{1}(t), \theta_{2}(t)\), respectively. As the runners go around the track both \(\theta_{1}(t)\) and \(\theta_{2}(t)\) change with time.

Figure 16.9: Figure for Exercises 30 and 31.

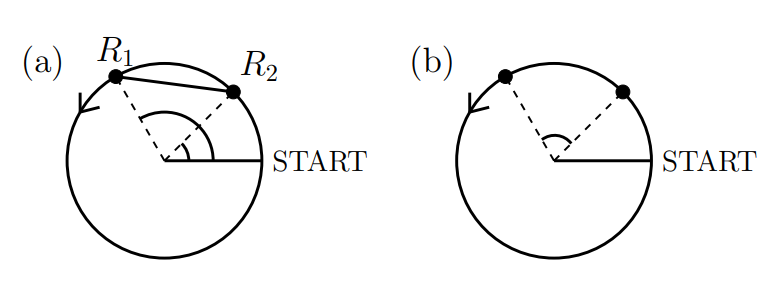
(a) At what rate it the angle \(\phi=\theta_{1}-\theta_{2}\) changing?

(b) What is the angle \(\phi\) at \(t=25 \mathrm{~s}\) ?

(c) What is the distance between the runners at \(t=25 \mathrm{~s}\) ?

Note: here "distance" refers to the length of the straight line connecting the runners.

(d) At what rate is the distance between the runners changing at \(t=25 \mathrm{~s}\) ? (a)

16.31. Phase angle and synchrony. Suppose that the same two runners as in Exercise 30 would speed up or slow down depending on the angle between them, \(\phi\) (see Figure 16.9). Then \(\phi=\phi(t)\) changes with time. We assume that the angle \(\phi\) satisfies a differential equation of the form

\[\frac{d \phi}{d t}=A-B \sin (\phi) \nonumber \]

where \(A, B>0\) are constants.

(a) What values of \(\phi\) correspond to steady states (i.e. constant solutions) of this differential equation?

(b) What restriction should be placed on the constants \(A, B\) for these steady states to exist?

(c) Suppose \(A=1, B=2\). Sketch the graph of \(f(\phi)=A-B \sin (\phi)\) fo \(-\pi \leq \phi \leq \pi\) and use it to determine what happens if the two runners start at the same point, \((\phi=0)\) at time \(t=0\).

16.32. Tumor mass. Figure \(16.10\) (not drawn to scale) shows a tumor mass containing a necrotic (dead) core (radius \(r_{2}\) ), surrounded by a layer of actively dividing tumor cells. The entire tumor can be assumed to be spherical, and the core is also spherical.

Figure 16.10: Figure for Exercise 32; tumor mass.

Note

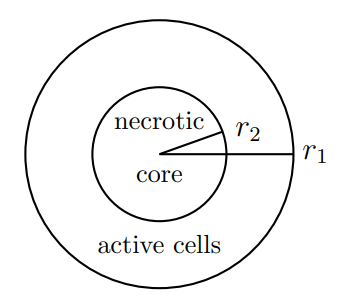
Formula.

Note that the volume and surface area of a sphere are \(V=(4 / 3) \pi r^{3}, S=4 \pi r^{2}\).

(a) If the necrotic core increases at the rate \(3 \mathrm{~cm}^{3} / y e a r\) and the volume of the active cells increases by \(4 \mathrm{~cm}^{3} /\) year, at what rate is the outer radius of the tumor \(\left(r_{1}\right)\) changing when \(r_{1}=1 \mathrm{~cm}\). (Leave your answer as a fraction in terms of \(\pi\); indicate units with your answer.) The angles in (a) are \(\theta_{1}(t), \theta_{2}(t)\). In (b), the angle between the runners is \(\phi\).

(b) At what rate (in \(\mathrm{cm}^{2} / \mathrm{yr}\) ) does the outer surface area of the tumor increase when \(r_{1}=1 \mathrm{~cm}\) ?

16.33. Blood vessel branching. Shown in Figure \(16.11\) is a major artery, (radius \(R\) ) and one of its branches (radius \(r\) ). A labeled schematic diagram is also shown (right). The length \(0 A\) is \(L\), and the distance between 0 and \(P\) is \(d\), where \(0 P\) is perpendicular to \(0 A\). The location of the branch point \((B)\) is to be determined so that the total resistance to blood flow in the path \(A B P\) is as small as possible. \((R, r, d, L\) are positive constants, and \(R>r\).)

Figure 16.11: Figure for Exercise 33; blood vessel branching.

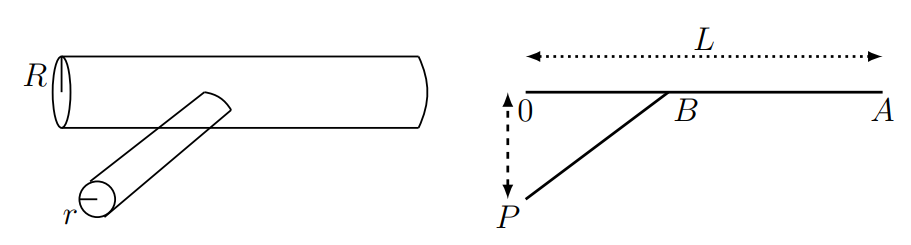
(a) Let the distance between 0 and \(B\) be \(x\). What is the length of the segment \(B A\) and what is the length of the segment \(B P\) ?

(b) The resistance of any blood vessel is proportional to its length and inversely proportional to its radius to the fourth power Based on this fact, what is the resistance, \(T_{1}\), of segment \(B A\) and what is the resistance, \(T_{2}\), of the segment \(B P\) ?

(c) Find the value of the variable \(x\) for which the total resistance, \(T(x)=\) \(T_{1}+T_{2}\) is a minimum.

16.34. Implicit differentiation. A surface that looks like an "egg carton" as depicted in Figure 16.12(a) can be described by the function

\[z=\sin (x) \cos (y) \nonumber \]

The intersection of this surface with the plane \(z=1 / 2\) is a curve (also called a level curve). One such level curve is shown in Figure \(16.12(b)\)

Figure 16.12: (a) The surface \(\sin (x) \cos (y)=\) z. (b) One level curve for this surface is shown on its own, and then enlarged, with some tangent lines. The tangent line to this level curve at the point \((\pi / 2, \pi / 3)\) is horizontal.

Note

Formula.

Note that " \(z\) is inversely proportional to \(y\) " means that \(z=k / y\) for some constant \(k\).

(a) Use implicit differentiation to find the slope of the tangent line to a point on such a curve.

(b) Find the slope of the tangent line to the same level curve at the point \(x=\frac{\pi}{2}\).

(c) Find the slope of the tangent line to the same level curve at the point \(x=\frac{\pi}{4}\).