7.4: Translations and Rotations

For convenience the ellipses, parabolas and hyperbolas in the previous sections were centered at the origin and had their foci on one of the coordinate axes. In general, the center and foci of those curves can be moved anywhere by means of coordinate transformations.

TranslationContinue editing

You have probably seen in earlier courses how the graph of a function \(y=f(x)\) can be shifted horizontally by an amount \(h\) and vertically by an amount \(k\) by replacing \(x\) and \(y\) by \(x-h\) and \(y-k\), respectively:

 

\[y - k ~=~ f(x-h) \nonumber \]

Figure \(\PageIndex{1}\): Translation

This coordinate transformation is called translation, and can be applied to any curve in the \(xy\)-plane. The origin \(O=(0,0)\) is shifted to the point \(O'=(h,k)\), which serves as the origin of the \(x'y'\)-plane,⁹ as in Figure \(\PageIndex{1}\). Let \(P=(x,y)\) be a point in the \(xy\)-plane. Consider \(P\) as a point \(P'=(x',y')\) in the \(x'y'\)-plane, so that relative to the origin \(O'\), the \(x'\) and \(y'\) coordinates of \(P'\) are:

 

\[\begin{aligned} x' ~&=~ x - h\\ y' ~&=~ y - k\end{aligned} \nonumber \]

Using these translation equations (i.e. the substitutions \(x \mapsto x-h\) and \(y \mapsto y-k\)), the graphs of the conic sections can be translated to any center \((h,k)\):

Note

9. The prime symbol (′ ) does not indicate differentiation—it acts merely to distinguish the new axes.

Ellipse:

For \(a>b>0\), an equation of the form

\[
\frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}=1
\nonumber \]

describes an ellipse with center \((h, k)\), vertexes \((h \pm a, k)\), and foci \((h \pm c, k)\), where \(c^2=a^2-b^2\). The eccentricity is \(e=\frac{c}{a}\), and the principal axis is the line \(y=k\).
Likewise, an equation of the form

\[
\frac{(y-k)^2}{a^2}+\frac{(x-h)^2}{b^2}=1
\nonumber \]

describes an ellipse with center \((h, k)\), vertexes \((h, k \pm a)\), and foci \((h, k \pm c)\), where \(c^2=a^2-b^2\). The eccentricity is \(e=\frac{c}{a}\), and the principal axis is the line \(x=h\).

Parabola:

For \(p \neq 0\), an equation of the form

\[
(x-h)^2=4 p(y-k)
\nonumber \]

describes a parabola with vertex \((h, k)\) and focus \((h, k+p)\). The directrix is the line \(y=k-p\) and the axis is the line \(x=h\).
Likewise, an equation of the form

\[
(y-k)^2=4 p(x-h)
\nonumber \]

describes a parabola with vertex \((h, k)\) and focus \((h+p, k)\). The directrix is the line \(x=h-p\) and the axis is the line \(y=k\)

Hyperbola:

For \(a \neq 0\) and \(b \neq 0\), an equation of the form

\[
\frac{(x-h)^2}{a^2}-\frac{(y-k)^2}{b^2}=1
\nonumber \]

describes a hyperbola with center \((h, k)\), vertexes \((h \pm a, k)\), and foci \((h \pm c, k)\), where \(c^2=\) \(a^2+b^2\). The eccentricity is \(e=\frac{c}{a}\), the directrices are the lines \(x=h \pm \frac{a^2}{c}\), the asymptotes are the lines \(y-k= \pm \frac{b}{a}(x-h)\), and the transverse axis is the line \(y=k\).
Likewise, an equation of the form

\[
\frac{(y-k)^2}{a^2}-\frac{(x-h)^2}{b^2}=1
\nonumber \]

describes a hyperbola with center \((h, k)\), vertexes \((h, k \pm a)\), and foci \((h, k \pm c)\), where \(c^2=\) \(a^2+b^2\). The eccentricity is \(e=\frac{c}{a}\), the directrices are the lines \(y=k \pm \frac{a^2}{c}\), the asymptotes are the lines \(y-k= \pm \frac{a}{b}(x-h)\), and the transverse axis is the line \(x=h\).

Example \(\PageIndex{1}\): ptrans1

Find the vertexes and foci of the ellipse \(\frac{(x-2)^2}{4} + (y-1)^2 = 1\)..

Solution

The translation coordinates are \((h,k)=(2,1)\). Also, \(a=2\) and \(b=1\). Thus, the vertexes are \((h \pm a,k) = (2 \pm 2,1) = (0,1)\) and \((4,1)\). Since \(c^2=a^2-b^2 = 3\) then \(c=\sqrt{3}\), so the foci are \((h \pm c,k) = (2 \pm \sqrt{3},1)\), as shown in Figure \(\PageIndex{2}\).

Note that the ellipse \(\frac{(x-2)^2}{4} + (y-1)^2 = 1\) in the \(xy\)-plane is the ellipse \(\frac{x'^2}{4} + y'^2 = 1\) in the \(x'y'\)-plane, for the translation equations \(x'=x-2\) and \(y'=y-1\) (i.e. the \(x'\)-axis is the line \(y=1\) and the \(y'\)-axis is the line \(x=2\)).

Figure \(\PageIndex{2}\): Ellipse \({(x-2)^2 \above 1pt 4} + (y-1)^2=1\)

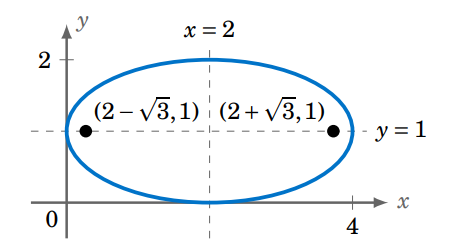
Example \(\PageIndex{2}\)

For \(a \ne 0\) and constants \(b\) and \(c\), find the vertex, focus and directrix of the parabola \(y=ax^2+bx+c\).

Solution

The idea here is to write \(y=ax^2+bx+c\) in the form \((x-h)^2 = 4p(y-k)\) for some \(h\), \(k\), and \(p\), by completing the square:

 

\[
\begin{aligned}
a x^2+b x+c & =y \\
a\left(x^2+\frac{b}{a} x\right) & =y-c \\
a\left(x^2+\frac{b}{a} x+\frac{b^2}{4 a^2}\right) & =y-c+a \frac{b^2}{4 a^2} \\
\left(x+\frac{b}{2 a}\right)^2 & =\frac{1}{a}\left(y+\frac{b^2-4 a c}{4 a}\right)
\end{aligned}
\nonumber \]

So \(h=-\frac{b}{2 a}, k=\frac{4 a c-b^2}{4 a}\), and \(4 p=\frac{1}{a}\) means \(p=\frac{1}{4 a}\). Thus, the vertex is \((h, k)=\left(-\frac{b}{2 a}, \frac{4 a c-b^2}{4 a}\right)\), the focus is \((h, k+p)=\left(-\frac{b}{2 a}, \frac{4 a c-b^2+1}{4 a}\right)\), and the directrix is the line \(y=k-p=\frac{4 a c-b^2-1}{4 a}\).

Rotation

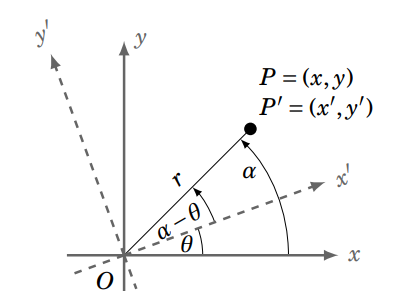
Rotation is another common coordinate transformation. Consider the case of rotating the \(xy\)-plane about the origin by an angle \(\theta\), as in Figure \(\PageIndex{3}\). The origin of the resulting \(x'y'\)-plane is unchanged from the origin \(O=(0,0)\) of the \(xy\)-plane. To find the rotation equations for \(x'\) and \(y'\), let \(P=(x,y)\) be a point in the \(xy\)-plane away from the origin. From trigonometry you know that for \(r=\sqrt{x^2+y^2} \ne 0\) and the angle \(0\circ \le \alpha < 360\circ\) measured from the positive \(x\)-axis to \(OP\),

Figure \(\PageIndex{3}\): Rotation

 

\[x ~=~ r\,\cos\,\alpha \quad\text{and}\quad y ~=~ r\,\sin\,\alpha ~.\qquad\qquad \nonumber \]

Considering \(P\) as a point \(P'=(x',y')\) in the \(x'y'\)-plane, \(OP'\) makes an angle \(\alpha - \theta\) with the positive \(x'\)-axis, so that by the sine and cosine subtraction identities,

 

\[\begin{aligned} x' ~&=~ r\,\cos\,(\alpha - \theta) ~=~ r\,\cos\,\alpha\;\cos\,\theta ~+~ r\,\sin\,\alpha\;\sin\,\theta ~=~ x\,\cos\,\theta ~+~ y\,\sin\,\theta\label{eqn:xrotate}\\ \text{and } y' ~&=~ r\,\sin\,(\alpha - \theta) ~=~ r\,\sin\,\alpha\;\cos\,\theta ~-~ r\,\cos\,\alpha\;\sin\,\theta ~=~ y\,\cos\,\theta ~-~ x\,\sin\,\theta\label{eqn:yrotate} ~.\end{aligned} \]

Similar to the translation substitutions, the above rotation equations allow any curve in the \(xy\)-plane to be rotated:

To rotate a curve in the \(x y\)-plane about the origin by an angle \(\theta\), make the following substitutions:

\[
x \mapsto x \cos \theta+y \sin \theta \text { and } y \mapsto-x \sin \theta+y \cos \theta
\nonumber \]

Example \(\PageIndex{3}\):

Find the equation of the ellipse \(\frac{x^2}{4} + y^2 = 1\) when rotated \(45\circ\) counterclockwise about the origin. Simplify the equation.

Solution

Find the equation of the ellipse \(\frac{x^2}{4}+y^2=1\) when rotated \(45^{\circ}\) counterclockwise about the origin. Simplify the equation.
Solution: For \(\theta=45^{\circ}\) the substitutions are:

 

\[
\begin{array}{l}
x \mapsto x \cos \theta+y \sin \theta=x \cos 45^{\circ}+y \sin 45^{\circ}=\frac{x+y}{\sqrt{2}} \\
y \mapsto-x \sin \theta+y \cos \theta=-x \sin 45^{\circ}+y \cos 45^{\circ}=\frac{-x+y}{\sqrt{2}}
\end{array}
\nonumber \]

The equation of the rotated ellipse (shown in Figure \(\PageIndex{4}\)) is then:

Figure \(\PageIndex{4}\)

 

\[
\begin{aligned}
\frac{1}{4}\left(\frac{x+y}{\sqrt{2}}\right)^2+\left(\frac{-x+y}{\sqrt{2}}\right)^2 & =1 \\
x^2+2 x y+y^2+4\left(x^2-2 x y+y^2\right) & =8 \\
5 x^2-6 x y+5 y^2-8 & =0
\end{aligned}
\nonumber \]

 

In the above example note the presence of the \(6xy\) term in the equation of the rotated ellipse. In general if a conic section has a second-degree equation of the form

 

\[Ax^2 ~+~ Bxy ~+~ Cy^2 ~+~ Dx ~+~ Ey ~+~ F ~=~ 0\label{eqn:degreetwo} \]

then \(B \ne 0\) indicates rotation, and either \(D \ne 0\) or \(E \ne 0\) indicates translation.

Example \(\PageIndex{4}\):

Find the value of \(a\) such that rotating the hyperbola \(\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1\) by \(45\circ\) counterclockwise about the origin results in the curve \(xy=1\).

Solution

Since \( \theta=45^{\circ}\) then as in Example } 7.3 the substitutions are again:

\[
x \mapsto \frac{x+y}{\sqrt{2}} \text { and } y \mapsto \frac{-x+y}{\sqrt{2}}
\nonumber \]

The equation of the rotated hyperbola is then:

\[
\begin{aligned}
\frac{1}{a^2}\left(\frac{x+y}{\sqrt{2}}\right)^2-\frac{1}{a^2}\left(\frac{-x+y}{\sqrt{2}}\right)^2 & =1 \\
\frac{x^2+2 x y+y^2-\left(x^2-2 x y+y^2\right)}{2 a^2} & =1 \\
\frac{2 x y}{a^2} & =1
\end{aligned}
\nonumber \]

Thus, when \(a=\sqrt{2}\) the rotated hyperbola has the equation \(x y=1\), which shows that the curve \(y=\frac{1}{x}\) is a hyperbola. In general any curve of the form \(B x y=1\) is a hyperbola for \(B \neq 0\).

The following result can be used for determining the type of conic section described by a second-degree equation:¹⁰

Note

10. For a proof see Section 6.8 in PROTTER, M.H. AND C.B. MORREY, Analytic Geometry, 2nd ed., Reading, MA: Addison-Wesley Publishing Company, Inc., 1975.

The graph of \(A x^2+B x y+C y^2+D x+E y+F=0\) (with \(A, B, C\) not all zero) describes a curve whose type is based on the sign of \(B^2-4 A C\) :

(a) \(B^2-4 A C<0\) : an ellipse (or a circle, point, or no curve)

(b) \(B^2-4 A C=0\) : a parabola (or a line, two parallel lines, or no curve)

(c) \(B^2-4 A C>0\) : a hyperbola (or two intersecting lines)

If \(B \neq 0\) and the curve is a conic section, then the rotation angle \(\theta\) is given by:

(a) \(\theta=45^{\circ}\) if \(A=C\)

(b) \(\tan 2 \theta=\frac{B}{A-C}\) if \(A \neq C\), with \(0^{\circ}<\theta<90^{\circ}\)

Recall that the rotation equations (7.7) and (7.8) for \(x^{\prime}\) and \(y^{\prime}\) in terms of \(x\) and \(y\) provided substitutions that allowed the second-degree equation of the rotated conic section to be found. Conversely, to transform a second-degree equation in \(x\) and \(y\) into a "standard" conic section equation in terms of \(x^{\prime}\) and \(y^{\prime}\) (to simplify sketching the graph), the "reverse" rotation equations for \(x\) and \(y\) in terms of \(x^{\prime}\) and \(y^{\prime}\) are needed:

\[
\begin{array}{l}
x=x^{\prime} \cos \theta-y^{\prime} \sin \theta \\
y=x^{\prime} \sin \theta+y^{\prime} \cos \theta
\end{array}
\nonumber \]

Example \(\PageIndex{5}\):

Determine the type of curve whose equation is \(5x^2+4xy+8y^2-36=0\), and sketch its graph.

Solution

Since \(A=5\), \(B=4\), and \(C=8\), then \(B^2-4AC = -144 < 0\), so the curve is an ellipse if it is a conic section. Since \(B \ne 0\) and \(A \ne C\), the rotation angle \(\theta\) would be given by \(\tan\,2\theta = \frac{B}{A-C} = \frac{4}{-3}\), with \(0\circ < \theta < 90\circ\). Then \(2\theta\) is in the second quadrant, so that \(\sin\,2\theta = \frac{4}{5}\) and \(\cos\,2\theta = \frac{-3}{5}\). Use a half-angle identity to find \(\theta\):

 

\[
\tan \theta=\frac{\sin 2 \theta}{1+\cos 2 \theta}=\frac{\frac{4}{5}}{1+\frac{-3}{5}}=2
\nonumber \]

Hence, \(\sin \theta=\frac{2}{\sqrt{5}}\) and \(\cos \theta=\frac{1}{\sqrt{5}}\). Now use equations (7.11) and (7.12) to get expressions for \(x\) and \(y\) in terms of \(x^{\prime}\) and \(y^{\prime}\) :

\[
\begin{array}{l}
x=x^{\prime} \cos \theta-y^{\prime} \sin \theta=\frac{x^{\prime}-2 y^{\prime}}{\sqrt{5}} \\
y=x^{\prime} \sin \theta+y^{\prime} \cos \theta=\frac{2 x^{\prime}+y^{\prime}}{\sqrt{5}}
\end{array}
\nonumber \]

Substitute those expressions into \(5 x^2+4 x y+8 y^2-36=0\) :

\[
\begin{aligned}
5\left(\frac{x^{\prime}-2 y^{\prime}}{\sqrt{5}}\right)^2+4\left(\frac{x^{\prime}-2 y^{\prime}}{\sqrt{5}}\right)\left(\frac{2 x^{\prime}+y^{\prime}}{\sqrt{5}}\right)+8\left(\frac{2 x^{\prime}+y^{\prime}}{\sqrt{5}}\right)^2-36 & =0 \\
45 x^{\prime 2}+20 y^{\prime 2} & =180 \\
\frac{x^{\prime 2}}{4}+\frac{y^{\prime 2}}{9} & =1
\end{aligned}
\nonumber \]

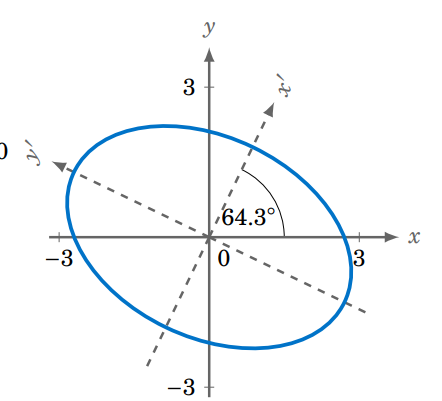
So the curve's equation in the \(x^{\prime} y^{\prime}\)-plane is \(\frac{x^{\prime 2}}{4}+\frac{y^{\prime 2}}{9}=1\). This is just the ellipse \(\frac{x^2}{4}+\frac{y^2}{9}=1\) rotated counterclockwise by the angle \(\theta=\tan ^{-1} 2 \approx 63.4^{\circ}\), as shown in the figure below.

Figure \(\PageIndex{5}\): Copy and Paste Caption here. (Copyright; author via source)

Exercises

For Exercises 1-3, sketch the graph of the given ellipse with the exact locations of the foci and vertexes.

1. \(\dfrac{(x-3)^2}{25}+\dfrac{(y-2)^2}{16}=1\)

2. \(\dfrac{(x+1)^2}{9}+\dfrac{(y+3)^2}{4}=1\)

3. \(4x^2 + y^2 + 24x - 2y + 21 = 0\vphantom{\dfrac{(x-3)^2}{25}+\dfrac{(y-2)^2}{16}=1}\)

For Exercises 4-7, sketch the graph of the given parabola with the exact locations of the focus, vertex and directrix. [[1.]]

4. \(4(x-1)^2 = 3(y+2)\)

5. \(y=4x^2 + 24x + 21\)

6. \(3(y+2)^2 = 5(x-2)\)

7. \(4x^2 - 4x + 4y - 5 = 0\)

For Exercises 8-10, sketch the graph of the given hyperbola with the exact locations of the foci, vertexes, directrices, and asymptotes.

8. \(\dfrac{(x-3)^2}{25}-\dfrac{(y-2)^2}{16}=1\)

9. \(\dfrac{(x+1)^2}{9}-\dfrac{(y+3)^2}{4}=1\)

10. \(4x^2 - y^2 + 24x - 2y + 21 = 0\vphantom{\dfrac{(x-3)^2}{25}-\dfrac{(y-2)^2}{16}=1}\)

11. Find the foci, vertexes, directrices and asymptotes for the hyperbola \(y=\frac{1}{x}\) in Example \(\PageIndex{5}\)

12. Find the equation of the parabola \(4y=x^2\) when rotated \(60\circ\) counterclockwise about the origin.

13. Prove equations \(\PageIndex{11}\) and (\(\PageIndex{12}\). (Hint: Use equations (\(\PageIndex{7}\) and \(\PageIndex{8}\)

14. Determine the type of curve whose equation is \(8x^2-12xy+17y^2-20=0\), and sketch its graph.

15, Determine the type of curve whose equation is \(7x^2+6xy-y^2-32=0\), and sketch its graph.

16. Let \(A'x'^2+B'x'y'+C'y'^2+D'x'+E'y'+F'=0\) be the equation obtained by substituting the “reverse” translation equations \(x=x'+h\) and \(y=y'+k\) into equation \(\PageIndex{10}\). Show that \(A=A'\), \(B=B'\) and \(C=C'\) (i.e. \(A\), \(B\) and \(C\) are invariant under translation).

17. Similar to Exercise 16, substitute the “reverse” rotation equations ([eqn:xprotate]) and ([eqn:yprotate]) into equation ([eqn:degreetwo]) to show that \(A+C\) and \(B^2-4AC\) are invariant under rotation.

18. Sketch the graph of the conic section whose equation is \(x^2-2 x y+y^2+4 x+4 y+10=0\). (Hint: First handle the rotation (since \(A=C\) use \(\theta=45^{\circ}\) even though \(B^2-4 A C=0\) ), then the translation (by completing the square).)