4.6: Homework- Optimization

Last updated
Save as PDF

Page ID: 88662

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Samantha has some whiskey at a party, and (being a science and math geek) estimates her blood alcohol content (BAC) follows the function:
$BAC(t) = \frac{0.25 t}{e^t},$

where $t$ is measured in hours after her first drink. Graph this function, and determine the following using a derivative:
1. How quickly is her BAC increasing (or decreasing) 15 minutes after her first drink?
  $BAC'(t) = \frac{0.25 - 0.25t}{e^t}$, (grams per dL per hour).
  ans
2. How quickly is her BAC increasing (or decreasing) 1 hour after her first drink?
  $0$ change
  ans
3. How quickly is her BAC increasing (or decreasing) 2 hours after her first drink?
  $\approx 0.034$ grams per dL per hour
  ans
Graph each function over the given interval. Use calculus to determine the location of all global and local mins and maxes.
1. $f(x) = -x^2 + 5x - 2$ on the interval $[0, 5]$.
  Local and Global Mins: $(0, -2), (5, -2)$, Local and global max: $(2.5, 4.25)$
  ans
2. $f(x) = x^2 - 6x + 10$ on the interval $[2, 6]$.
  Local min: $(2, 2)$, global and local min: $(3, 1)$, local and global max: $(6, 10)$
  ans
3. $f(x) = x^3 - 6x^2 + 11x - 6$ on the interval $[0, 3]$.
  Local and global maximum at $(1.42, 0.38 )$, Local min: $(2.58,-0.38 )$, local and global minimum: $(0, -6)$, local maximum: $(3, -2)$
  ans
4. $f(x) = x^3-5 x^2+8 x-4$ on the interval $[0, 2.5]$.
  Local max at $x = 0.75$, local min at $x = 2$, global max at $x = 2.5$, global min at $x = 0$.
  ans
5. $f(x) = x^4 - 16x$ on the interval $[0, 3]$.
  Local max at $x = 0$, global min at $x = \sqrt[3]{4}$, global max at $x = 3$
  ans
6. $f(x) = \frac{x^2}{x + 1}$ on the interval $[-3, 3]$.
  Local min at $x = -3$, local max at $x = -2$, local min at $x = 0$, local max at $x = 3$
  ans
Using a chemotherapy drug on a petri-dish of cancer cells, it is found that $P(x)$ percent more of the cancer cells are killed using $x$ milligrams of drug per square centimeter than healthy cells, where $x$ ranges from $0$ to $4$. It is thought
$P(x) = x^3-8 x^2+16 x$

For what value of $x$ is $P(x)$ maximized?

$quicklatex.com-b8a57ab2026731e3ad99b44c428a20a5_l3.png$
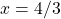ans
Bananas as we know them may be doomed! Suppose the fungus Tropical Race 4 mentioned in the article is killing off bananas on an island in Jamaica. The number of viable banana farms starts at $16000$, with $800$ being forced to close per year. But new banana farms are according to the function $20e^{0.3t}$ with new varieties immune to the fungus ($t$ measured in years). So the total number of viable banana farms is
$V(t) = 16000- 800t + 20e^{0.3t}$

on the interval $[0, 20]$. At what point is the number of banana farms minimized? What is the number of viable banana farms at this point?

This function is minimized at $t \approx 16.3$ with the number of banana farms at $5619$
ans
The area of a rectangle is length times width. A farmer needs to build a pig pen against the side of the barn using $20$ meters of fence. What is the maximum amount of area he can enclose?
$pen.svgfixme$
Watch the KhanAcademy videos on maximizing the area of a box:
Optimizing Box Volume Graphically and
Optimizing Box Volume Analytically
An open-topped box is formed by removing the square corners of sidelength $x$ off of a $40$ in by $80$ in piece of cardboard, and folding each side up. What value of $x$ maximizes the volume of the box?
$x \approx 8.45$
ans
The height and radius of a cone together add to $5$ inches. What value of the radius maximizes the volume? The volume is given by $V = \frac{1}{3} \pi r^2 h$.
in
ans