3.9: Inverse Trigonometric Functions

We now turn our attention to finding derivatives of inverse trigonometric functions. These derivatives will prove invaluable in the study of integration later in this text. The derivatives of inverse trigonometric functions are quite surprising in that their derivatives are actually algebraic functions. Previously, derivatives of algebraic functions have proven to be algebraic functions and derivatives of trigonometric functions have been shown to be trigonometric functions. Here, for the first time, we see that the derivative of a function need not be of the same type as the original function.

Example \(\PageIndex{4A}\): Derivative of the Inverse Sine Function

Use the inverse function theorem to find the derivative of \(g(x)=\sin^{−1}x\).

Solution

Since for \(x\) in the interval \(\left[−\frac{π}{2},\frac{π}{2}\right],f(x)=\sin x\) is the inverse of \(g(x)=\sin^{−1}x\), begin by finding \(f′(x)\). Since

\[f′(x)=\cos x \nonumber \]

and

\[f′\big(g(x)\big)=\cos \big( \sin^{−1}x\big)=\sqrt{1−x^2} \nonumber \]

we see that

\[g′(x)=\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{f′\big(g(x)\big)}=\dfrac{1}{\sqrt{1−x^2}} \nonumber \]

Analysis

To see that \(\cos(\sin^{−1}x)=\sqrt{1−x^2}\), consider the following argument. Set \(\sin^{−1}x=θ\). In this case, \(\sin θ=x\) where \(−\frac{π}{2}≤θ≤\frac{π}{2}\). We begin by considering the case where \(0<θ<\frac{π}{2}\). Since \(θ\) is an acute angle, we may construct a right triangle having acute angle \(θ\), a hypotenuse of length \(1\) and the side opposite angle \(θ\) having length \(x\). From the Pythagorean theorem, the side adjacent to angle \(θ\) has length \(\sqrt{1−x^2}\). This triangle is shown in Figure \(\PageIndex{2}\) Using the triangle, we see that \(\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}\).

Figure \(\PageIndex{2}\): Using a right triangle having acute angle \(θ\), a hypotenuse of length \(1\), and the side opposite angle \(θ\) having length \(x\), we can see that \(\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}\).

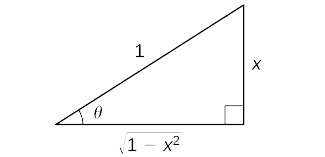
In the case where \(−\frac{π}{2}<θ<0\), we make the observation that \(0<−θ<\frac{π}{2}\) and hence

\(\cos\big(\sin^{−1}x\big)=\cos θ=\cos(−θ)=\sqrt{1−x^2}\).

Now if \(θ=\frac{π}{2}\) or \(θ=−\frac{π}{2},x=1\) or \(x=−1\), and since in either case \(\cosθ=0\) and \(\sqrt{1−x^2}=0\), we have

\(\cos\big(\sin^{−1}x\big)=\cosθ=\sqrt{1−x^2}\).

Consequently, in all cases,

\[\cos\big(\sin^{−1}x\big)=\sqrt{1−x^2}.\nonumber \]

Example \(\PageIndex{4B}\): Applying the Chain Rule to the Inverse Sine Function

Apply the chain rule to the formula derived in Example \(\PageIndex{4A}\) to find the derivative of \(h(x)=\sin^{−1}\big(g(x)\big)\) and use this result to find the derivative of \(h(x)=\sin^{−1}(2x^3).\)

Solution

Applying the chain rule to \(h(x)=\sin^{−1}\big(g(x)\big)\), we have

\(h′(x)=\dfrac{1}{\sqrt{1−\big(g(x)\big)^2}}g′(x)\).

Now let \(g(x)=2x^3,\) so \(g′(x)=6x^2\). Substituting into the previous result, we obtain

\(\begin{align*} h′(x)&=\dfrac{1}{\sqrt{1−4x^6}}⋅6x^2\\[4pt]&=\dfrac{6x^2}{\sqrt{1−4x^6}}\end{align*}\)

Exercise \(\PageIndex{4}\)

Use the inverse function theorem to find the derivative of \(g(x)=\tan^{−1}x\).

Hint

The inverse of \(g(x)\) is \(f(x)=\tan x\). Use Example \(\PageIndex{4A}\) as a guide.

Answer

\(g′(x)=\dfrac{1}{1+x^2}\)

The derivatives of the remaining inverse trigonometric functions may also be found by using the inverse function theorem. These formulas are provided in the following theorem.

Derivatives of Inverse Trigonometric Functions

\[\begin{align} \dfrac{d}{dx}\big(\sin^{−1}x\big) &=\dfrac{1}{\sqrt{1−x^2}} \label{trig1} \\[4pt] \dfrac{d}{dx}\big(\cos^{−1}x\big) &=\dfrac{−1}{\sqrt{1−x^2}} \label{trig2} \\[4pt] \dfrac{d}{dx}\big(\tan^{−1}x\big) &=\dfrac{1}{1+x^2} \label{trig3} \\[4pt] \dfrac{d}{dx}\big(\cot^{−1}x\big) &=\dfrac{−1}{1+x^2} \label{trig4} \\[4pt] \dfrac{d}{dx}\big(\sec^{−1}x\big) &=\dfrac{1}{|x|\sqrt{x^2−1}} \label{trig5} \\[4pt] \dfrac{d}{dx}\big(\csc^{−1}x\big) &=\dfrac{−1}{|x|\sqrt{x^2−1}} \label{trig6} \end{align} \]

Example \(\PageIndex{5A}\): Applying Differentiation Formulas to an Inverse Tangent Function

Find the derivative of \(f(x)=\tan^{−1}(x^2).\)

Solution

Let \(g(x)=x^2\), so \(g′(x)=2x\). Substituting into Equation \ref{trig3}, we obtain

\(f′(x)=\dfrac{1}{1+(x^2)^2}⋅(2x).\)

Simplifying, we have

\(f′(x)=\dfrac{2x}{1+x^4}\).

Example \(\PageIndex{5B}\): Applying Differentiation Formulas to an Inverse Sine Function

Find the derivative of \(h(x)=x^2 \sin^{−1}x.\)

Solution

By applying the product rule, we have

\(h′(x)=2x\sin^{−1}x+\dfrac{1}{\sqrt{1−x^2}}⋅x^2\)

Exercise \(\PageIndex{5}\)

Find the derivative of \(h(x)=\cos^{−1}(3x−1).\)

Hint

Use Equation \ref{trig2}. with \(g(x)=3x−1\)

Answer

\(h′(x)=\dfrac{−3}{\sqrt{6x−9x^2}}\)

Example \(\PageIndex{6}\): Applying the Inverse Tangent Function

The position of a particle at time \(t\) is given by \(s(t)=\tan^{−1}\left(\frac{1}{t}\right)\) for \(t≥ \ce{1/2}\). Find the velocity of the particle at time \( t=1\).

Solution

Begin by differentiating \(s(t)\) in order to find \(v(t)\).Thus,

\(v(t)=s′(t)=\dfrac{1}{1+\left(\frac{1}{t}\right)^2}⋅\dfrac{−1}{t^2}\).

Simplifying, we have

\(v(t)=−\dfrac{1}{t^2+1}\).

Thus, \(v(1)=−\dfrac{1}{2}.\)

Exercise \(\PageIndex{6}\)

Find the equation of the line tangent to the graph of \(f(x)=\sin^{−1}x\) at \(x=0.\)

Hint

\(f′(0)\) is the slope of the tangent line.

Answer

\(y=x\)