1.2: Volume by Discs and Washers
- Page ID
- 503
Volumes of Revolution
Suppose you wanted to make a clay vase. It is made by shaping the clay into a curve and spinning it along an axis. If we want to determine how much water it will hold, we can consider the cross sections that are perpendicular to the axis of rotation, and add up all the volumes of the small cross sections. We have the following definition:
\[ \text{Volume} = \int_a^b A(x) dx \]
where \(A(x)\) is the area the cross section at a point \(x\).
Example 1
Find the volume of the solid that is produced when the region bounded by the curve
\[ y = x^2, \; y = 0\; ,\text{ and } x = 2 \nonumber\]
is revolved around the x-axis.
Solution
Since we are revolving around the x-axis, we have that the cross section is in the shape of a disk with radius equal to the y-coordinate of the point.
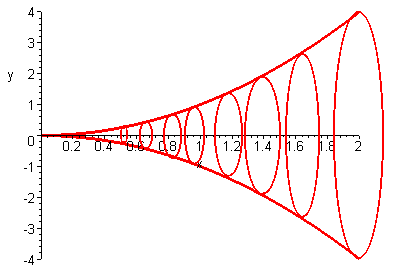
Hence
\[ A(x) = \pi r^2 = \pi (x^2)^2. \nonumber \]
We have
\[ \begin{align*} \text{ Volume} &= \int_{0}^{2} \pi (x^2)^2 dx \\ &= \left( \dfrac{\pi}{5}x^5 \right]_{0}^{2} \\ &= \dfrac{32 \pi}{5}. \end{align*}\]
Example 2
Find the volume of the solid formed be revolving the region between the curves
\[ y = x^2 \text{ and } y = \sqrt{x} \nonumber\]
about the x-axis.
Solution
We draw the picture and revolve a cross section about the x-axis and come up with a washer. The area of the washer is equal to the area of the outer disk minus the area of the inner disk.
\[ A = \pi (R^2 - r^2) \nonumber\]
We have that \(R\) is the y-coordinate of the top curve and \(r\) is the y-coordinate of the bottom curve \( x^2\). We have
\[ A = \pi([\sqrt{x}]^2 - [x^2]^2) = \pi[x - x^4] \nonumber\]
Hence
\[ \begin{align*} Volume &= \int _0^1 \pi \left( x-x^4 \right) \,dx \\ &= \pi \left[\dfrac{x^2}{2} - \dfrac{x^5}{5} \right]_0^1 \\ &= \dfrac{3 \pi}{10}. \end{align*} \]
Example 3: Revolving about the y-axis
Find the volume of the solid that is formed by revolving the curve bounded by
\[ y = x \text{ and } y = \sqrt{x}. \nonumber \]
about the y-axis.
Solution
This time our cross section is perpendicular to the y-axis. When we revolve, we get a washer with \(R\) equal to the x-coordinate of the\( y = \sqrt{x} \) curve and \(r\) equal to the x-coordinate of the \(y = x\) curve.
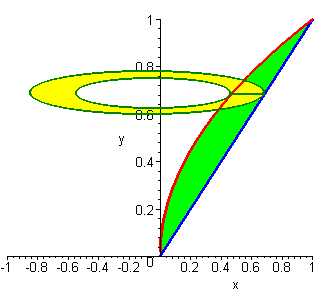
Hence
\[ A = \pi\left(\left(y\right)^2 - \left(y^2\right)^2\right) = \pi \left(y^2 - y^4\right). \nonumber\]
We get
\[ \begin{align*} \text{Volume} &= \int_0^1 \pi(y^2-y^4) dy \\ &= \pi\left(\dfrac{y^3}{3}-\dfrac{y^5}{5}\right]_0^1\\ &= \dfrac{2\pi}{15}. \end{align*} \]
Revolving About a Non-axis Line
Example 4
Find the volume of the region formed by revolving the curve
\[y=x^3 \;\;\; 0<x<2 \nonumber\]
about the line \(y=-2 \)
Solution
This time we revolve the cross-section and obtain a disk. The radius of the disk is 2 plus the y-coordinate of the curve.
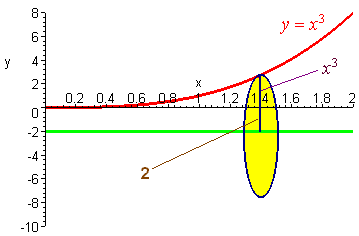
Hence
\[ A = \pi (2 + x^3)^2 \nonumber\]
so that
\[ \text{Volume} = \int _0^2 \pi (2 + x^3)^2 \, dx. \nonumber\]
This integral can be evaluated by FOIL-ing out the binomial and then integrating each monomial. We get a value of approximately 133.
Example 5
Try revolving the curve
\[ y =x^2 \nonumber\]
from 0 to 2 about the line \( x = 5 \).
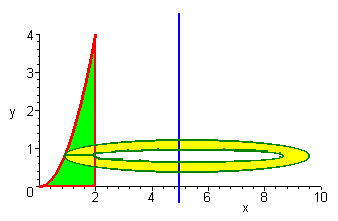
We have
\[ A = \pi \left[\left(5 - \sqrt{y} \right)^2 - 9\right] \nonumber \]
so that
\[ \text{Volume} = \int_0^4 \pi \left[ \left( 5 - \sqrt{y} \right)^2 -9 \right] dy. \nonumber \]
This integral works out to be approximately 59.
Applications of Volume
Example 6: The Volume of the Khufu Pyramid
The base of the Khufu pyramid is a square with wide length 736 feet and the angle that the base makes with the ground is 50.8597 degrees. Find the volume of the Khufu pyramid.
Solution
First note that we need to change to radian measure.
\[ 50.8597^{\circ} = 0.88767 \text{ radians} \nonumber\]
The height of the pyramid is
\[ 736 \tan(0.88767) = 904.348. \nonumber\]
We have that the area of a cross section is \(s^2\)where \(s\) is the side length of the square. Placing the y-axis through the top of the pyramid and the origin at the middle of the base, we have that
\[ s = \sqrt{2} x. \nonumber\]
Hence
\[ A(x) = 2x^2. \nonumber\]
Since the axis perpendicular to the cross sections is the y-axis, we need \(A\) in terms of \(y\). We set up similar triangles:
\[ \dfrac{x}{736} = \dfrac{y}{904.348} \nonumber\]
\[ x = 0.8138\, y. \nonumber\]
Hence
\[ A(y) = 1.3247\, x^2 \nonumber \]
We calculate
\[ \int _0^{904.35} 1.3247\, x^2\, dx = 361,131\; \text{ cubic feet}. \nonumber \]
Example 7
A sphere is formed by rotation the curve
\[ y= \sqrt{r^2 - x^2}. \nonumber \]
We have
\[ \begin{align*} \text{Volume} &= \int_{-r}^{r} \pi (\sqrt{r^2-x^2})^2 dx \\ &= \int_{-r}^{r} \pi (r^2-x^2) dx \\ &= \pi \left( r^2x-\dfrac{x^2}{3} \right]_{-r}^r \\ &= \pi \Big[ \big( r^3-\dfrac{r^3}{3}\big) - \big( -r^3+\dfrac{r^3}{3} \big) \Big] \\ &= \dfrac{4}{3} \pi r^3\end{align*}.\]
Exercise
Two cylinders of radius \(r\) intersect each other at right angles. Find the volume of their intersection.
Hint: Consider cross sections parallel to both axes of rotation. These cross sections are squares. Then show that the side length is \( 2\sqrt{r^2 - x^2} \)
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


