4.7: Surface Integrals
- Page ID
- 572
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Up until this point we have been integrating over one dimensional lines, two dimensional domains, and finding the volume of three dimensional objects. In this section we will be integrating over surfaces, or two dimensional shapes sitting in a three dimensional world. These integrals can be applied to real world situations such as finding the upward force on an open parachute.
Introduction
In the last section, we learned how to find the surface area for parametric surfaces. We cut the region in the uv-plane into tiny rectangles and added up the area of the corresponding tiny parallelograms in the xy-plane. The area of these parallelograms was
\[ \Delta A = \left|r_u \times r_v \right| \Delta u \Delta v\nonumber \]
If we think of the surface as having varying density \(f(x,y,z)\), then the mass of this parallelogram will be
\[\Delta M = f(x(u,v),y(u,v),z(u,v)) ||r_u \times r_v || \Delta u \Delta v \nonumber \]
and adding up all these masses and taking the limit as the rectangle sizes approach zero, gives the definition of the surface integral.
To compute the integral of a surface, we extend the idea of a line integral for integrating over a curve. Although surfaces can fluctuate up and down on a plane, by taking the area of small enough square sections we can essentially ignore the fluctuations and treat is as a flat rectangle. Over time the area of the surface can successfully be calculated by taking small enough sections, much like what you learned with Reimann sums previously. The surface integral can be calculated in one of three ways depending on how the surface is defined. All three are valid and can be used interchangeably, but depending on how the surfaces are described, one integral will be easier to solve than the others. The integrals from the above methods are typically impossible or very difficult to analytically solve, but can easily solved numerically.
Surface Integral: Parametric Definition
For a smooth surface \(S\) defined parametrically as \(r(u,v) = f(u,v)\hat{\textbf{i}} + g(u,v) \hat{\textbf{j}} + h(u,v) \hat{\textbf{k}} , (u,v) \in R \), and a continuous function \(G(x,y,z)\) defined on \(S\), the surface integral of \(G\) over \(S\) is given by the double integral over \(R\):
\[ \iint_{S} G(x,y,z)\, d\sigma = \iint_{R} G(f(u,v), g(u,v), h(u,v)) |r_{u} \times r_{v}| \, du \,dv .\nonumber \]
Surface Integral: implicit Definition
For a surface \(S\) given implicitly by \( F(x,y,z) = c \), where \(F\) is a continuously differentiable function, with \(S\) lying above its closed and bounded shadow region \(R\) in the coordinate plane beneath it, the surface integral of the continuous function \(G\) over \(S\) is given by the double integral \(R\),
\[ \iint_{S} G(x,y,z)d\sigma = \iint_{R} G(x,y,z) \frac{|\nabla F|}{|\nabla F \cdot p|} dA ,\nonumber \]
where \(p\) is a unit vector normal to \(R\) and \( \nabla F \cdot p \neq 0\).
Surface Integral: explicit Definition
For a surface \(S\) given explicitly as the graph of \(z = f(x,y)\), where \(f\) is a continuously differentiable function over a region \(R\) in the \(xy\)-plane, then the parameterization
\[ {\textbf{r}}(u,v) = u \hat{\textbf{i}} + v\hat{\textbf{j}} + f(u,v)\hat{\textbf{k}}\nonumber \]
has the property that
\[ \left| \textbf{r}_u \times \textbf{r}_v \right| = \sqrt{f_{x}^{2} + f_{y}^{2} + 1}\nonumber \]
So the surface integral of the continuous function \(G\) over \(S\) is given by the double integral over \(R\),
\[ \iint_{S} G(x,y,z)\,d\sigma = \iint_{R} G(x,y, f(x,y)) \sqrt{f_{x}^{2} + f_{y}^{2} + 1} \,dx\, dy. \nonumber \]
We call a smooth surface \(S\) orientable or two-sided if it is possible to define a field \(\textbf{n}\)of unit normal vectors on \(S\) that varies continuously with position. All parts of an orientable surface are orientable. Spheres and other smooth closed surfaces in space are orientable. In general, we choose \(\textbf{n}\) on a closed surface to point outward.
Example \(\PageIndex{1}\)
Integrate the function \( H(x,y,z) = 2xy + z \) over the plane \( x + y + z = 2 \).
Solution
First, let's draw out the plane.
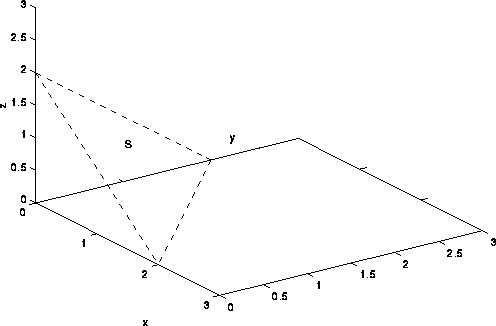
Next, notice the equation of the plane can be manipulated. Thus, we can put it in the explicit form \( z = 2 - x - y \). This gives us the integral
\[ \iint_{S} H(x,y,z)\,d \sigma = \iint_{R} H(x,y,z) \sqrt{f_{x}^{2} + f_{y}^{2} + 1} \,dA. \nonumber\nonumber \]
Take the partial derivatives of \(x\) and \(y\) of the surface. In this case, \(f_x = -1\) and \(f_y = -1\). Substitute these values into the integral along with \(H(x,y,z)\) with \(z = 2 - x - y \) to get the integral
\[ \iint_{R} (2xy + 2 - x - y) \sqrt{ (-1)^{2} + (-1)^{2} + 1 }\, dA. \nonumber\nonumber \]
In order to determine the bounds for the integral, we need to compress the surface to 2-dimensions, or look at its "shadow region". The idea is to imagine looking at the above graph from above, down the \(z\)-axis. Thus, you will be looking at the \(xy\) plane and the surface will look like the triangle bordered by the \(x\)-axis, \(y\)-axis, and the equation \(y = 2 - x \). This yields the integral
\[ \int_{0}^{2} \int_{0}^{2-x} (2xy + 2 - x - y) \sqrt{ (-1)^{2} + (-1)^{2} + 1 }\,dy\,dx .\nonumber\nonumber \]
Now we can solve this integral just like any other double integral
\[\begin{align*} & \sqrt{3} \int_{0}^{2} \int_{0}^{2-x} 2xy + 2 - x - y \, dy\, dx \\ &= \sqrt{3} \int_{0}^{2} \left[ xy^2 + 2y - xy - \frac{y^{2}}{2} \right]_{0} ^{2 - x} dx \\ &= \sqrt{3} \int_{0}^{2} x(2-x)^2 - x(2-x) - \frac{(2-x)^{2}}{2} dx \\ &= \sqrt{3} \int_{0}^{2} 4x - 4x^{2} + x^{3} - 2x + x^{2} - 2 + 2x - \frac{x^{2}}{2} dx \\ &= \sqrt{3} \int_{0}^{2} x^{3} - \frac{7x^{2}}{2} + 4x - 2 dx \\ &= \left. \sqrt{3} \left( \frac{x^4}{4} - \frac{7x^3}{6} + 2x^2 - 2x \right) \right|_0^2 \\ &= \sqrt{3} \left(16 - \frac{56}{6} \right) . \end{align*}\nonumber \]
Example \(\PageIndex{2}\)
Find
\[ \iint_S f(x,y,z)\,dS \nonumber\nonumber \]
where \(S\) is the surface
\[ r(u,v) = u\hat{\textbf{i}} + u2\hat{\textbf{j}}+ (u+ v) \hat{\textbf{k}} \nonumber\nonumber \]
with \( 0 \le u \le 2 \) and \(1 \le v \le 4\) and \( f(x,y,z) = x + 2z\).
Solution
We find the partial derivatives
\[ \textbf{r}_u = \hat{\textbf{i}}+ (2u)\hat{\textbf{j}}+ \hat{\textbf{k}} \nonumber\nonumber \]
\[ \textbf{r}_v = \hat{\textbf{k}} \nonumber\nonumber \]
and take the cross product
\[\begin{align*} ||r_u \times r_v || &= \begin{vmatrix} \hat{\textbf{i}} &\hat{\textbf{j}} &\hat{\textbf{k}} \\[4pt] 1 &2u &1 \\[4pt] 0 &0 &1 \end{vmatrix} \\[4pt] &= ||2u \hat{\textbf{i}} - \hat{\textbf{j}} || \\[4pt] &= \sqrt{1+4u^2}. \end{align*} \nonumber \]
We have
\[\begin{align*} f(x(u,v),y(u,v),z(u,v)) &= x(u,v) +2z(u,v) \\[4pt] &= u +2(u + v) \\[4pt] &= 3u + v. \end{align*} \nonumber \]
We find
\[\int_3^4\int_2^6 (3u +2v)\sqrt{1+4u^2}\, dv\,du.\nonumber \nonumber \]
Although this integral is possible, its solution is quite involved. You can verify that the surface integral evaluates to \( \approx 525.27\).
Example \(\PageIndex{3}\)
Find
\[ \iint_S f(x,y,z)\,dS\nonumber\nonumber \]
where \(S\) is the part of the paraboloid
\[ z = x^2 + y^2 \nonumber\nonumber \]
that lies inside the cylinder
\[ x^2 + y^2 = 1 \nonumber\nonumber \]
and
\[ f(x,y,z) = z.\nonumber\nonumber \]
Solution
We have
\[ \sqrt{1+g_x^2 +g_y^2} = \sqrt{1+4x^2 + 4y^2}\nonumber\nonumber \]
and
\[ f(x,y,z) = z = x^2 + y^2 . \nonumber\nonumber \]
At this point, you should be thinking, "This looks like a job for polar coordinates." And we get
\[ \int_0^{2\pi}\int_0^1 r^2\sqrt{1+4r^2} \, r\,dr\,d\theta.\nonumber\nonumber \]
Let
\( u = 1 + 4r^2\) and \(du = 8r\, dr\) with \(r^2 = \dfrac{1}{4} u - \dfrac{1}{4}\)
and the substitution gives us
\[ \dfrac{1}{32} \int_0^{2pi}\int_0^5 (u-1)u^{1/2} \, dr\,d\theta = \dfrac{1}{32} \int_0^{2\pi} \left[ \dfrac{2}{5} u^{5/2} - \dfrac{2}{3} u^{3/2} \right]_1^5 \, d\theta \approx 2.98\nonumber\nonumber \]
Oriented Surfaces
We have seen how a region \(R\) with boundary curve \(C\) can be oriented. Traveling along \(C\), we look to see if the region is on the right or left. Unfortunately, this definition does not work will for surfaces in three dimensions. The idea of right and left is not well defined. In fact not all surfaces can be oriented. We say that a surface is orientable if a unit normal vector can be defined on the surface such that it varies continuously over the surface. Below is an example of a non-orientable surface (called the Möbius Strip). You can see that there is no front or back of this surface.

Contributors and Attributions
- Michael Rea (UCD)
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


