3.6: Functions

One very, very important type of relation is called a function. Some mathematicians treat functions totally separately from relations, but I think it’s more useful to think of a function as a special kind of relation. Many of the ideas are the same, as you’ll see.

Think back to the relations between wizards and soft drinks. One such relation (we called it \(R\)) had (Harry, Mt. Dew) and (Ron, Mt. Dew) in it. Another one (\(S\)) contained (Hermione, Mt. Dew), (Hermione, Dr. Pepper), and (Harry, Dr. Pepper). Since there were three wizards and two soft drinks, we calculated that there were \(2^6\) such relations.

Now some of those relations have exactly one ordered pair for each wizard. For instance, the relation \(F\) which contains { (Harry, Dr. Pepper), (Ron, Mt. Dew), (Hermione, Mt. Dew) }. This kind of relation is a function. It associates each element of the first set with exactly one element of the second set. Obviously not all relations are functions: \(R\), for example, is not (there’s no pair with Hermione) and neither is \(S\) (there’s more than one pair with Hermione). But those that do form a very special class of interest, and warrant a whole new terminology.

When we have a function \(F\) between a set \(X\) and \(Y\), we write \(F : X \rightarrow Y\) to indicate this. The set \(X\) is called the domain of the function, and the set \(Y\) is called the codomain. The colon and the arrow are just there to complete the syntax. The rule with functions is very simple: every element of the domain is related to exactly one element of the codomain. Sometimes we say that a domain element is “mapped" to its corresponding codomain element. Note very carefully that the reverse is not necessarily true. In fact, with the wizards-and-drinks example, it can’t possibly be true: there are fewer drinks than wizards, so some drink is bound to be related to more than one wizard. (Think about it.) It’s also perfectly legit to have a function like { (Harry, Dr. Pepper), (Ron, Dr. Pepper), (Hermione, Dr. Pepper) }, where some element(s) of the codomain are left out altogether.

One of the things that makes functions useful is that we can ask “which element of \(Y\) goes with \(X\)?" and we will always get back a well-defined answer. We can’t really do that with relations in general, because the answer might be “none" or “several." Take a look back at the \(R\) and \(S\) examples, above: what answer would we get if we asked “which drink goes Hermione map to?" for either relation? Answer: there is no answer.

But with functions, I can freely ask that question because I know I’ll get a kosher answer. With \(F\), I can ask, “which drink does Hermione map to?" and the answer is “Mt. Dew." In symbols, we write this as follows:

\(F\)(Hermione) = Mt. Dew

This will look familiar to computer programmers, since it resembles a function call. In fact, it is a function call. That’s exactly what it is. “Functions" in languages like C++ and Java were in fact named after this discrete math notion. And if you know anything about programming, you know that in a program I can “call the F() function" and “pass it the argument ‘Hermione’" and “get the return value ‘Mt.Dew.’" I never have to worry about getting more than one value back, or getting none at all.

You might also remember discussing functions in high school math, and the so-called “vertical line test." When you plotted the values of a numerical function on a graph, and there was no vertical (up-and-down) line that intersected more than one point, you could safely call the plot a “function." That’s really exactly the same thing as the condition I just gave for functions, stated graphically. If a plot passes the vertical line test, then there is no \(x\) value for which there’s more than one \(y\) value. This means it makes sense to ask “which is the value of \(y\) for a particular value of \(x\)?" You’ll always get one and only one answer. (There’s no such thing, of course, as a “horizontal line test," since functions are free to map more than one \(x\) value to the same \(y\) value. They just can’t do the reverse.)

The difference between the functions of high school math and the functions we’re talking about here, by the way, is simply that our functions aren’t necessarily numeric. Sometimes we do draw “plots" of sorts, though, like this one:

Figure \(\PageIndex{1}\): A function represented graphically.

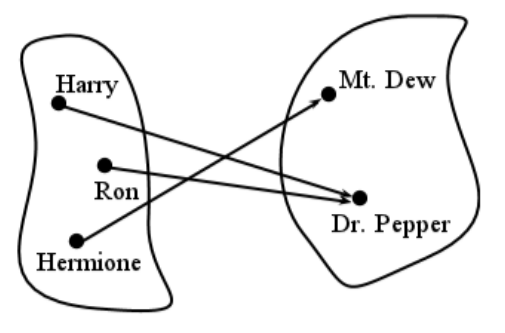
This simply shows which elements of the domain map to which elements of the codomain. The left blob is the domain, the right blob is the codomain, and there’s an arrow representing each mapping.

Now as with relations, functions normally have “meaning." We could define a function called “firstTasted" that associates each wizard with the soft drink he or she first sampled as a child. We could define another called “faveDrink" that maps each wizard to his or her favorite — presuming that every wizard has a favorite drink in the set (Hermione will have to overlook her iced tea and choose among the options provided). A third function called “wouldChooseWithMexicanFood" provides information about which drink each wizard provides with that type of cuisine. Here are Ron’s values for each of the three functions:

firstTasted(Ron) = Mt. Dew
faveDrink(Ron) = Mt. Dew
wouldChooseWithMexicanFood(Ron) = Dr. Pepper

These values indicate that Mt. Dew was the soda pop that Ron first sipped, and it has been his favorite ever since, although at La Estrellita he prefers a Pepper.

Functions can be defined intensionally or extensionally, just as with relations. Intensionally, we provide the conceptual meaning of what the function represents. Extensionally, we list the values for each element of the domain.

One other term that applies to every function is its range. A function’s range is the subset of the codomain that at least one element the domain actually maps to. It’s the part of the codomain that’s “reachable." For instance, if the function \(G : X \rightarrow Y\) is { (Harry, Dr. Pepper), (Ron, Dr. Pepper), (Hermione, Dr. Pepper) }, then even though the codomain is { Dr. Pepper, Mt. Dew } the range is merely { Dr. Pepper }. That’s because there isn’t any ordered pair that contains Mt. Dew, so it’s left out of the range. You can’t “reach" Mt. Dew via the \(G\) function by starting with any of its inputs, so it’s left out in the cold.

By the way, a function’s range is sometimes called its image. These terms are synonymous.