6.6: Inverse Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
A bijection is a function that is both one-to-one and onto. Naturally, if a function is a bijection, we say that it is bijective. If a function f:A→B is a bijection, we can define another function g that essentially reverses the assignment rule associated with f. Then, applying the function g to any element y from the codomain B, we are able to obtain an element x from the domain A such that f(x)=y. Let us refine this idea into a more concrete definition.
Definition: inverse function
Let f:A→B be a bijective function. Its inverse function is the function f−1:B→A with the property that f−1(b)=a⇔b=f(a). The notation f−1 is pronounced as “f inverse.” See Figure 6.6.1 for a pictorial view of an inverse function.
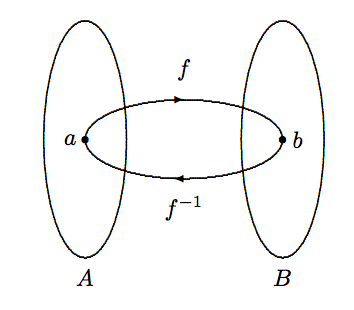
Why is f−1:B→A a well-defined function? For it to be well-defined, every element b∈B must have a unique image. This means given any element b∈B, we must be able to find one and only one element a∈A such that f(a)=b. Such an a exists, because f is onto, and there is only one such element a because f is one-to-one. Therefore, f−1 is a well-defined function.
If a function f is defined by a computational rule, then the input value x and the output value y are related by the equation y=f(x). In an inverse function, the role of the input and output are switched. Therefore, we can find the inverse function f−1 by following these steps:
- Interchange the role of x and y in the equation y=f(x). That is, write x=f(y).
- Solve for y. That is, express y in terms of x. The resulting expression is f−1(x).
Be sure to write the final answer in the form f−1(x)=…. Do not forget to include the domain and the codomain, and describe them properly.
Example 6.6.1
To find the inverse function of f:R→R defined by f(x)=2x+1, we start with the equation y=2x+1. Next, interchange x with y to obtain the new equation x=2y+1. Solving for y, we find y=12(x−1). Therefore, the inverse function is f−1:R→R,f−1(x)=12(x−1). It is important to describe the domain and the codomain, because they may not be the same as the original function.
Example 6.6.2
The function s:[−π2,π2]→[−1,1] defined by s(x)=sinx is a bijection. Its inverse function is
s−1:[−1,1]→[−π2,π2],s−1(x)=arcsinx.
The function arcsinx is also written as sin−1x, which follows the same notation we use for inverse functions.
hands-on Exercise 6.6.1
The function f:[−3,∞)→[0,∞) is defined as f(x)=√x+3. Show that it is a bijection, and find its inverse function
hands-on Exercise 6.6.2
Find the inverse function of g:R→(0,∞) defined by g(x)=ex.
Remark
Exercise caution with the notation. Assume the function f:Z→Z is a bijection. The notation f−1(3) means the image of 3 under the inverse function f−1. If f−1(3)=5, we know that f(5)=3. The notation f−1({3}) means the preimage of the set {3}. In this case, we find f−1({3})={5}. The results are essentially the same if the function is bijective.
If a function g:Z→Z is many-to-one, then it does not have an inverse function. This makes the notation g−1(3) meaningless. Nonetheless, g−1({3}) is well-defined, because it means the preimage of {3}. If g−1({3})={1,2,5}, we know g(1)=g(2)=g(5)=3.
In general, f−1(D) means the preimage of the subset D under the function f. Here, the function f can be any function. If f is a bijection, then f−1(D) can also mean the image of the subset D under the inverse function f−1. There is no confusion here, because the results are the same.
Example 6.6.3
The function f:R→R is defined as f(x)={3x if x≤1, 2x+1 if x>1. Find its inverse function.
- Solution
-
Since f is a piecewise-defined function, we expect its inverse function to be piecewise-defined as well. First, we need to find the two ranges of input values in f−1. The images for x≤1 are y≤3, and the images for x>1 are y>3. Hence, the codomain of f, which becomes the domain of f−1, is split into two halves at 3. The inverse function should look like f−1(x)={??? if x≤3, ??? if x>3. Next, we determine the formulas in the two ranges. We find
f−1(x)={13x if x≤3, 12(x−1) if x>3. The details are left to you as an exercise.
hands-on Exercise 6.6.3
Find the inverse function of g:R→R defined by g(x)={3x+5 if x≤6, 5x−7 if x>6. Be sure you describe g−1 properly.
Example 6.6.4
The function g:Z10→Z10 is defined by g(x)≡7x+2 (mod 10). Find its inverse function.
- Solution
-
From x=g(y)≡7y+2 (mod 10), we obtain y≡7−1(x−2)≡3(x−2)(mod10). Hence, the inverse function g−1:Z10→Z10 is defined by g−1(x)≡3(x−2) (mod 10).
hands-on Exercise 6.6.4
The function h:Z57→Z57 defined by h(x)≡49x−3 (mod 57). Find its inverse function.
Example 6.6.5
Define h:Z10→Z10 according to h(x)=2(x+3)mod. Does h^{-1} exist?
- Solution
-
Since 2^{-1} does not exist, we suspect the answer is no. In fact, h(x) is always even, and it is easy to verify that \text{im}h = \{0,2,4,6,8\}. Since h is not onto, h^{-1} does not exist.
Example \PageIndex{6}\label{eg:invfcn-06}
Find the inverse function of f :{\mathbb{Z}}\to{\mathbb{N}\cup\{0\}} defined by f(n) = \cases{ 2n & if $n\geq0$, \cr -2n-1 & if $n < 0$. \cr} \nonumber
- Solution
-
In an inverse function, the domain and the codomain are switched, so we have to start with f^{-1}:\mathbb{N} \cup \{0\} \to \mathbb{Z} before we describe the formula that defines f^{-1}. Writing n=f(m), we find n = \cases{ 2m & if $m\geq0$, \cr -2m-1 & if $m < 0$. \cr} \nonumber We need to consider two cases.
- If n=2m, then n is even, and m=\frac{n}{2}.
- If n=-2m-1, then n is odd, and m=-\frac{n+1}{2}.
Therefore, the inverse function is defined by f^{-1}:\mathbb{N} \cup \{0\} \to \mathbb{Z} by:
f^{-1}(n) = \cases{ \frac{2}{n} & if $n$ is even, \cr -\frac{n+1}{2} & if $n$ is odd. \cr} \nonumber
Verify this with some numeric examples.
hands-on Exercise \PageIndex{5}\label{he:invfcn-05}
The function f :{\mathbb{Z}}\to{\mathbb{N}} is defined as f(n) = \cases{ -2n & if $n < 0$, \cr 2n+1 & if $n\geq0$. \cr} \nonumber Find its inverse.
Let A and B be finite sets. If there exists a bijection f :{A}{B}, then the elements of A and B are in one-to-one correspondence via f. Hence, |A|=|B|. This idea provides the basis for some interesting proofs.
Example \PageIndex{7}\label{eg:invfcn-07}
Let A=\{a_1,a_2,\ldots,a_n\} be an n-element sets. Recall that the power set \wp(A) contains all the subsets of A, and \{0,1\}^n = \{(b_1,b_2,\ldots,b_n) \mid b_i\in\{0,1\} \mbox{ for each $i$, where $1\leq i\leq n$} \}. \nonumber Define F:{\wp(A)}\to{\{0,1\}^n} according to F(S) = (x_1,x_2,\ldots,x_n), where x_i = \cases{ 1 & if $a_i\in S$, \cr 0 & if $a_i\notin S$. \cr} \nonumber Simply put, F(S) is an ordered n-tuple whose ith entry is either 1 or 0, indicating whether S contains the ith element of A (1 for yes, and 0 for no).
It is clear that F is a bijection. For n=8, we have, for example, F(\{a_2,a_5,a_8\}) = (0,1,0,0,1,0,0,1), \nonumber and F^{-1}\big((1,1,0,0,0,1,1,0)\big) = \{a_1,a_2,a_6,a_7\}. \nonumber The function F defines a one-to-one correspondence between the subsets of A and the ordered n-tuples in \{0,1\}^n. Since there are two choices for each entry in these ordered n-tuples, we have 2^n such ordered n-tuples. This proves that |\wp(A)|=2^n, that is, A has 2^n subsets.
hands-on Exercise \PageIndex{6}\label{he:invfcn-06}
Consider the function F defined in Example 6.6.7. Assume n=8. Find F(\emptyset) and F^{-1}\big( (1,0,1,1,1,0,0,0)\big).
Summary and Review
- A bijection is a function that is both one-to-one and onto.
- The inverse of a bijection f :{A}{B} is the function {f^{-1}}:{B}\to{A} with the property that f(x)=y \Leftrightarrow x=f^{-1}(y). \nonumber
- In brief, an inverse function reverses the assignment rule of f. It starts with an element y in the codomain of f, and recovers the element x in the domain of f such that f(x)=y.
Exercise \PageIndex{1}\label{ex:invfcn-01}
Which of the following functions are bijections? Explain!
- f :{\mathbb{R}}\to{\mathbb{R}}, f(x)=x^3-2x^2+1.
- g :{[\,2,\infty)}\to{\mathbb{R}}, g(x)=x^3-2x^2+1.
- h:{\mathbb{R}}\to{\mathbb{R}}, h(x)=e^{1-2x}.
- p :{\mathbb{R}}\to{\mathbb{R}}, p(x)=|1-3x|.
- q:{[\,2,\infty)}\to{[\,0,\infty)}, q(x)=\sqrt{x-2}.
Exercise \PageIndex{2}\label{ex:invfcn-02}
For those functions that are not bijections in the last problem, can we modify their codomains to change them into bijections?
Exercise \PageIndex{3}\label{ex:invfcn-03}
Let f and g be the functions from (1,3) to (4,7) defined by f(x) = \frac{3}{2}\,x+\frac{5}{2}, \qquad\mbox{and}\qquad g(x) = -\frac{3}{2}\,x+\frac{17}{2}. \nonumber Find their inverse functions. Be sure to describe their domains and codomains.
Exercise \PageIndex{4}\label{ex:invfcn-04}
Find the inverse function f :{\mathbb{R}}\to{\mathbb{R}} defined by f(x) = \cases{ 3x+5 & if $x\leq 6$, \cr 5x-7 & if $x > 6$. \cr} \nonumber
Be sure you describe f^{-1} correctly and properly.
Exercise \PageIndex{5}\label{ex:invfcn-05}
The function g :{[\,1,3\,]}\to{[\,4,\,7]} is defined according to g(x) = \cases{ x+3 & if $1\leq x< 2$, \cr 11-2x & if $2\leq x\leq 3$. \cr} \nonumber Find its inverse function. Be sure you describe it correctly and properly.
Exercise \PageIndex{6}\label{ex:invfcn-06}
Find the inverse of the function r :{(0,\infty)}\to{\mathbb{R}} defined by r(x)=4+3\ln x.
Exercise \PageIndex{7}\label{ex:invfcn-07}
Find the inverse of the function s :{\mathbb{R}}\to{(-\infty,-3)} defined by s(x)=4-7e^{2x}.
Exercise \PageIndex{8}\label{ex:invfcn-08}
Find the inverse of each of the following bijections.
- h:{\{1,2,3,4,5\}}\to{\{a,b,c,d,e\}}, h(1)=e, h(2)=c, h(3)=b, h(4)=a, h(5)=d.
- k :{\{1,2,3,4,5\}}\to{\{1,2,3,4,5\}}, k(1)=3, k(2)=1, k(3)=5, k(4)=4, k(5)=2.
Exercise \PageIndex{9}\label{ex:invfcn-09}
Find the inverse of each of the following bijections.
- u:{\mathbb{Q}}\to{\mathbb{Q}}, u(x)=3x-2.
- v:{\mathbb{Q}-\{1\}}\to{\mathbb{Q}-\{2\}}, v(x)=\frac{2x}{x-1}.
- w:{\mathbb{Z}}\to{\mathbb{Z}}, w(n)=n+3.
Exercise \PageIndex{10}\label{ex:invfcn-10}
Find the inverse of each of the following bijections.
- r :{\mathbb{Z}_{12}}\to{\mathbb{Z}_{12}}, r(n)\equiv 7n (mod 12).
- s :{\mathbb{Z}_{33}}\to{\mathbb{Z}_{33}}, s(n)\equiv 7n+5 (mod 33).
- t :{\mathbb{Z}}\to{\mathbb{N}\cup\{0\}}, t(n) = \cases{ 2n-1 & if $n > 0$, \cr -2n & if $n\leq0$,\cr}
Exercise \PageIndex{11}\label{ex:invfcn-11}
The images of the bijection {\alpha}:{\{1,2,3,4,5,6,7,8\}}\to{\{a,b,c,d,e,f,g,h\}} are given below. \begin{array}{|c||*{8}{c|}} \hline x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline \alpha(x)& g & a & d & h & b & e & f & c \\ \hline \end{array} \nonumber Find its inverse function.
Exercise \PageIndex{12}\label{ex:invfcn-12}
Below is the incidence matrix for the bijection {\beta}: {\{a,b,c,d,e,f\}}\to{\{x,y,z,u,v,w\}}. \begin{array}[t]{cc} & \begin{array}{cccccc} u & v & w & x & y & z \end{array} \\ \begin{array}{c} a \\ b \\ c \\ d \\ e \\ f \end{array} & \left(\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{array}\right) \end{array} \nonumber Find its inverse function.


