7.4: Partial and Total Ordering
- Page ID
- 8424
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two special relations occur frequently in mathematics. Both have to do with some sort of ordering of the elements in a set. A branch of mathematics is devoted to their study. As you can tell from the brief discussion in this section, they cover many familiar concepts.
A relation on a nonempty set \(A\) is called a partial ordering or a partial-order relation if it is reflexive, antisymmetric, and transitive. We often use \(\preceq\) to denote a partial ordering, and called \((A,\preceq)\) a partially ordered set or a poset.
Example \(\PageIndex{1}\label{eg:ordering-01}\)
The usual “less than or equal to” relation on \(R\), denoted \(\leq\), is a perfect example of partial ordering. In fact, this is the reason why we adopt the notation \(\preceq\), as it reflects the similarities between the two symbols.
Example \(\PageIndex{2}\label{eg:ordering-02}\)
Another classic example of partial ordering is the subset relation, denoted \(\subseteq\), on \(\wp(S)\), where \(S\) is any set of elements. Observe that \(S\) can be empty, in which case \(\wp(\emptyset) = \{\emptyset\}\), and \((\wp(\emptyset),\subseteq)\) is obviously a partially ordered set.
Example \(\PageIndex{3}\label{eg:ordering-03}\)
Another standard example of poset is \((\mathbb{N},\mid)\). It is easy to verify that the “divides” relation over the natural numbers is a partial ordering. Can you explain why \((\mathbb{Z}^*,\mid)\) is not a poset?
Exercise \(\PageIndex{1}\label{he:ordering-01}\)
Find a counterexample to illustrate why the “divides” relation, denoted \(\mid\) , over \(\mathbb{Z}^*\) is not antisymmetric. Is the “divides” relation reflexive over \(\mathbb{Z}\)? How about transitivity?
Exercise \(\PageIndex{2}\label{he:ordering-02}\)
Define the relation \(\sqsubseteq\) on \(\wp(\{a,b,c,d\})\) according to \[S\sqsubseteq T \,\Leftrightarrow\, S\subseteq T\cup\{a\}. \nonumber\] Is \((\wp(\{a,b,c,d\},\sqsubseteq)\) a poset? Which properties it does not possess? Explain.
Obviously, if \(a\preceq b\) but \(a\neq b\), then we can write \(a \prec b\). We sometimes say \(a\) precedes \(b\), or \(b\) succeeds \(a\). We also say \(a\) is the predecessor of \(b\), or \(b\) is the successor of \(a\).
The digraph for a poset can be simplified. Since \(a\) is always related to \(a\) itself, it is redundant to draw a loop around every vertex. Since \(a\preceq b\) and \(b\preceq c\) always imply that \(a\preceq c\), there is no need to include the arc (directed edge) from \(a\) to \(c\). So we follow the convention that we only draw an arc from \(a\) to \(b\) if \(a\prec b\) and there does not exist another element \(t\) such that \(a\prec t\) and \(t\prec b\). Lastly, if \(a\prec b\), we can place \(b\) above \(a\) so that all the arcs are pointing upward. This suggests that we can use undirected lines to make the graph easier to read. All these modifications lead to a much simpler graphical representation called a Hasse diagram.
Example \(\PageIndex{4}\label{eg:ordering-04}\)
It is clear that \((\{1,2,3,4,6,12\},\mid)\) is a poset. Its Hasse diagram is displayed below.
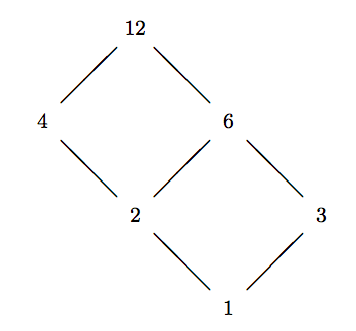
In this convention of using undirected line, the \(\preceq\) relation (hence, the ordering of the elements) is read from the bottom up.
Exercise \(\PageIndex{3}\label{he:ordering-03}\)
Draw the Hasse diagram for the poset \((\{1,2,3,4,6,9,12,18,36\},\mid)\).
The definition of a poset does not require every pair of distinct elements to be comparable. This means there may exist \(a\neq b\) such that \(a\not\preceq b\) and \(b\not\preceq a\). An example can be found in the numbers 2 and 3 in Example 7.4.4. If a partial ordering has the additional property that for any two distinct elements \(a\) and \(b\), either \(a\prec b\) or \(b\prec a\) (hence, any pair of distinct elements are comparable), we call the relation a total ordering.
Example \(\PageIndex{5}\label{eg:ordering-05}\)
The poset \((\mathbb{N},\leq)\) is a totally ordered set. The poset \((\{1,5,25,125\},\mid)\) is also a totally ordered set. Its Hasse diagram is shown below.
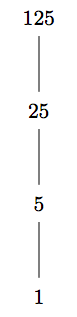
It is clear that the Hasse diagram of any totally ordered set will look like the one displayed above. Consequently, a total ordering is also called a linear ordering. A totally ordered set is also called a chain.
Exercise \(\PageIndex{4}\label{he:ordering-04}\)
Construct the Hasse diagram for the poset \((\{1,2,4,18,16\},\mid)\). Is it a totally ordered set?
Exercise \(\PageIndex{5}\label{he:ordering-05}\)
Construct the Hasse diagram for the poset \((\wp(\{a,b,c\}),\subseteq)\).
Summary and Review
- A relation that is reflexive, antisymmetric, and transitive is called a partial ordering.
- A set with a partial ordering is called a partially ordered set or a poset.
- A poset with every pair of distinct elements comparable is called a totally ordered set.
- A total ordering is also called a linear ordering, and a totally ordered set is also called a chain.
Exercise \(\PageIndex{1}\label{ex:ordering-01}\)
Let \(A\) be the set of natural numbers that are divisors of 30. Construct the Hasse diagram of \((A,\mid)\).
Exercise \(\PageIndex{2}\label{ex:ordering-02}\)
Let \(S = \big\{\{a\},\{b\},\{c\},\{a,b\},\{a,c\},\{b,c\}\big\}\). Construct the Hasse diagram for \((S,\subseteq)\).
Exercise \(\PageIndex{3}\label{ex:ordering-03}\)
Let \((A,\preceq)\) be a poset, and \(B\) a nonempty subset of \(A\). Show that \((B,\preceq)\) is also a poset. Naturally, we call \((B,\preceq)\) a subposet of \((A,\preceq)\).
Exercise \(\PageIndex{4}\label{ex:ordering-04}\)
Define the relation \(\preceq\) on \(\mathbb{Z}\) according to \[a\preceq b \,\Leftrightarrow\, a=b \mbox{ or } a\bmod3 < b\bmod3. \nonumber\]
- Show that \((\mathbb{Z},\preceq)\) is a poset.
- Let \(B=\{-3,-2,-1,0,1,2,-3\}\). Construct the Hasse diagram for the subposet \((B,\preceq)\).
Exercise \(\PageIndex{5}\label{ex:ordering-05}\)
Define the relation \(\preceq\) on \(\mathbb{Z}\) according to \[a\preceq b \,\Leftrightarrow\, a=b \mbox{ or } |a|<|b|. \nonumber\]
- Show that \((\mathbb{Z},\preceq)\) is a poset.
- Construct the Hasse diagram for the subposet \((B,\preceq)\), where \(B=\{-2,-1,0,1,2\}\).
Exercise \(\PageIndex{6}\label{ex:ordering-06}\)
Define the relation \(\preceq\) on \(\mathbb{Z}\times\mathbb{Z}\) according to \[(a,b)\preceq(c,d) \,\Leftrightarrow\, (a,b)=(c,d) \mbox{ or } a^2+b^2<c^2+d^2. \nonumber\]
- Show that \((\mathbb{Z}\times\mathbb{Z},\preceq)\) is a poset.
- Construct the Hasse diagram for the subposet \((B,\preceq)\), where \(B=\{0,1,2\}\times\{0,1,2\}\).
Exercise \(\PageIndex{7}\label{ex:ordering-07}\)
Construct an example of a subset \(B\) of \(\wp(\{a,b,c,d\})\) such that \((B,\subseteq)\) is a totally ordered set.
Exercise \(\PageIndex{8}\label{ex:ordering-08}\)
Let \[A = \{(m,n)\mid m,n\in\mathbb{N} \mbox{ and } \gcd(m,n)=1\}, \nonumber\] and define the relation \(\preceq\) on \(A\) according to \[(a,b)\preceq(c,d) \,\Leftrightarrow\, ad\leq bc. \nonumber\] Prove that \((A,\preceq)\) is a totally ordered set.


