2.1: Strings- A First Look

Let \(n\) be a positive integer. Throughout this text, we will use the shorthand notation \([n]\) to denote the \(n\)-element set \(\{1,2,...,n\}\). Now let \(X\) be a set. Then a function \(s:[n] \rightarrow X\) is also called an \(X\)-string of length \(n\). In discussions of \(X\)-strings, it is customary to refer to the elements of \(X\) as characters, while the element \(s(i)\) is the \(i^{th}\) character of \(s\). Whenever practical, we prefer to denote a string \(s\) by writing \(s = "x_1x_2x_3...x_n"\), rather than the more cumbersome notation \(s(1) = x_1, s(2) = x_2, ..., s(n) = x_n\).

There are a number of alternatives for the notation and terminology associated with strings. First, the characters in a string \(s\) are frequently written using subscripts as \(s_1,s_2,...,s_n\), so the \(i^{th}\)-term of \(s\) can be denoted \(s_i\) rather than \(s(i)\). Strings are also called sequences, especially when \(X\) is a set of numbers and the function \(s\) is defined by an algebraic rule. For example, the sequence of odd integers is defined by \(s_i = 2i - 1\).

Alternatively, strings are called words, the set \(X\) is called the alphabet and the elements of \(X\) are called letters. For example, \(aababbccabcbb\) is a 13-letter word on the 3-letter alphabet \(\{a,b,c\}\).

In many computing languages, strings are called arrays. Also, when the character \(s(i)\) is constrained to belong to a subset \(X_i \subseteq X\), a string can be considered as an element of the Cartesian product \(X_1 \times X_2 \times ... \times X_n\), which is normally viewed as \(n\)-tuples of the form \((x_1,x_2,...,x_n)\) such that \(x_i \in X_i\) for all \(i \in [n]\).

Example 2.1

In the state of Georgia, license plates consist of four digits followed by a space followed by three capital letters. The first digit cannot be a 0. How many license plates are possible?

Solution

Let \(X\) consist of the digits \(\{0,1,2,...,9\}\), let \(Y\) be the singleton set whose only element is a space, and let \(Z\) denote the set of capital letters. A valid license plate is just a string from

\((X - \{0\}) \times X \times X \times X \times Y \times Z \times Z \times Z\)

so the number of different license plates is \(9 \times 10^3 \times 1 \times 26^3 = 158 184 000\), since the size of a product of sets is the product of the sets' sizes. We can get a feel for why this is the case by focusing just on the digit part of the string here. We can think about the digits portion as being four blanks that need to be filled. The first blank has 9 options (the digits 1 through 9). If we focus on just the digit strings beginning with 1, one perspective is that they range from 1000 to 1999, so there are 1000 of them. However, we could also think about there being 10 options for the second spot, 10 options for the third spot, and 10 options for the fourth. Multiplying \(10 \times 10 \times 10\) gives \(1000\). Since our analysis of filling the remaining digit blanks didn't depend on our choice of a 1 for the first position, we see that each of the 9 choices of initial digit gives 1000 strings, for a total of \(9000 = 9 \times 10^3 \).

In the case that \(X = \{0,1\}\), an \(X\)-string is called a 0-1 string (also a binary string or bit string). When \(X = \{0,1,2\}\), an \(X\)-string is also called a ternary string.

Example 2.2

A machine instruction in a 32-bit operating system is just a bit string of length 32. Thus, there are 2 options for each of 32 positions to fill, making the number of such strings \(2^{32} = 4 294 967 296\). In general, the number of bit strings of length \(n\) is \(2^n\).

Example 2.3

Suppose that a website allows its users to pick their own usernames for accounts, but imposes some restrictions. The first character must be an upper-case letter in the English alphabet. The second through sixth characters can be letters (both upper-case and lower-case allowed) in the English alphabet or decimal digits (0–9). The seventh position must be ‘@’ or ‘.’. The eighth through twelfth positions allow lower-case English letters, ‘*’, ‘%’, and ‘#’. The thirteenth position must be a digit. How many users can the website accept registrations from?

Solution

We can visualize the options by thinking of the 13 positions in the string as blanks that need to be filled in and putting the options for that blank above. In Figure 2.4, we've used U to denote the set of upper-case letters, L for the set of lower-case letters, and D for the set of digits.

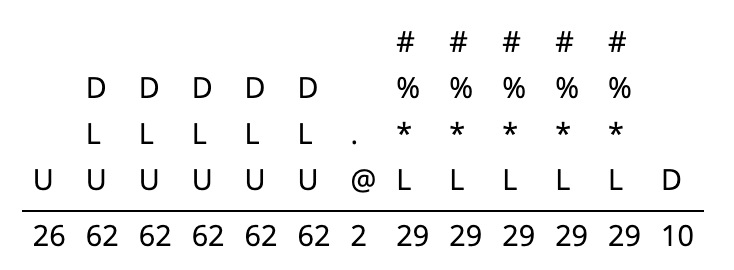
Figure 2.4: String Template

Below each position in the string, we've written the number of options for that position. (For example, there are 62 options for the second position, since there are 52 letters once both cases are accounted for and 10 digits. We then multiply these possibilities together, since each choice is independent of the others. Therefore, we have

\(26 \times 62^5 \times 2 \times 29^5 \times 10 = 9 771 287 890 863 360\)

total possible usernames.