6.5: The Subset Lattice

When \(X\) is a finite set, the family of all subsets of \(X\), partially ordered by inclusion, forms a subset lattice. We illustrate this in Figure 6.26 where we show the lattice of all subsets of {1,2,3,4}. In this figure, note that we are representing sets by bit strings, and we have further abbreviated the notation by writing strings without commas and parentheses.

Figure 6.26. A Subset Lattice

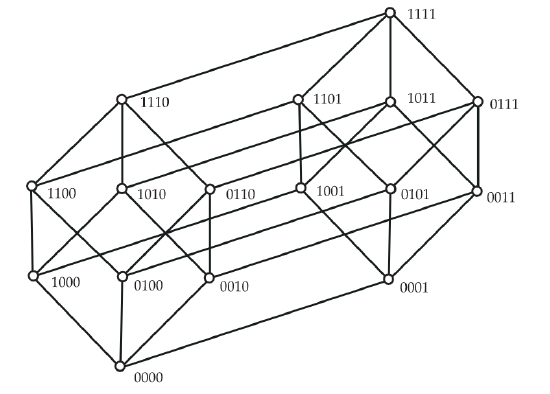
For a positive integer \(t\), we let \(2^t\) denote the subset lattice consisting of all subsets of \(\{1,2,…,t\}\) ordered by inclusion. Some elementary properties of this poset are:

1. The height is \(t+1\) and all maximal chains have exactly \(t+1\) points.
2. The size of the poset \(\textbf{2}^t\) is \(2^t\) and the elements are partitioned into ranks (antichains) \(A_0,A_1,…,A_t\) with \(|A_i|= \binom{t}{i}\) for each \(i=0,1,…,t\).
3. The maximum size of a rank in the subset lattice occurs in the middle, i.e. if \(s=⌊t/2⌋\), then the largest binomial coefficient in the sequence \( \binom{t}{0}, \binom{t}{1}, \binom{t}{2},…,\binom{t}{t}\) is \( \binom{t}{s}\). Note that when \(t\) is odd, there are two ranks of maximum size, but when \(t\) is even, there is only one.

6.5.1 Sperner's Theorem

For the width of the subset lattice, we have the following classic result of Sperner.

Theorem 6.27. Sperner's Theorem

For each \(t \geq 1\), the width of the subset lattice \(2^t\) is the maximum size of a rank, i.e.,

width\((\textbf{2}^t) = \dbinom{t}{⌊\frac{t}{2}⌋}\)

Proof

The width of the poset \(\textbf{2}^t\) is at least \(C(t,\frac{t}{2}⌋)\) since the set of all \(⌊\frac{t}{2}⌋\)-element subsets of \(\{1,2,…,t\}\) is an antichain. We now show that the width of \(\textbf{2}^t\) is at most \(C(t,⌊\frac{t}{2}⌋)\).

Let \(w\) be the width of \(\textbf{2}^t\) and let \(\{S_1,S_2,…,S_w\}\) be an antichain of size \(w\) in this poset, i.e., each \(S_i\) is a subset of \(\{1,2,…,t\}\) and if \(1 \leq i<j \leq w\), then \(S_i \nsubseteq S_j\) and \(S_j \nsubseteq S_i\).

For each \(i\), consider the set \(S_i\) of all maximal chains which pass through \(S_i\). It is easy to see that if \(|S_i|=k_i\), then \(|S_i|=k_i!(t−k_i)!\). This follows from the observation that to form such a maximum chain beginning with \(S_i\) as an intermediate point, you delete the elements of \(S_i\) one at a time to form the sets of the lower part of the chain. Also, to form the upper part of the chain, you add the elements not in \(S_i\) one at a time.

Note further that if \(1 \leq i<j \leq w\), then \(S_i \cap S_j= \emptyset\), for if there was a maximum chain belonging to both \(S_i\) and \(S_j\), then it would imply that one of Si and Sj is a subset of the other.

Altogether, there are exactly \(t!\) maximum chains in \(\textbf{2}^t\). This implies that

\(\displaystyle \sum_{i=1}^w k_i!(t-k_i)! \leq t!\).

This implies that

\( \displaystyle \sum_{i=1}^w \dfrac{k_i! (t - k_i)!}{t!}\) = \(\displaystyle \sum_{i=1}^w \dfrac{1}{\binom{t}{k_i}} \leq 1 \).

It follows that

\(\displaystyle \sum_{i=1}^{i=w} \dfrac{1}{\binom{t}{⌈\frac{t}{2}⌉}} \leq 1\).

Thus

\(w \leq \dbinom{t}{⌈\frac{t}{2}⌉}\).