15.6: Exercises

Last updated
Save as PDF

Page ID: 97968

Mitchel T. Keller & William T. Trotter
Georgia Tech & Morningside College

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Write the permutations shown below in cycle notation.

\begin{pmatrix}

1 & 2 & 3 & 4 & 5 & 6 \\

4 & 2 & 5 & 6 & 3 & 1

\end{pmatrix}

2. Compute $\pi_1 \pi_2, \pi_2 \pi_1, \pi_3 \pi_4$, and $\pi_4 \pi_3$ for the permutations $\pi_i$ in Exercise 15.6.1.

3. Find $stab_{D_8}⁡(C_3)$ and $stab_{D_8}⁡(C_{16})$ for the colorings of the vertices of the square shown in Figure 15.1 by referring to Figure 15.2.

4. In Figure 15.15, we show a regular pentagon with its vertices labeled. Use this labeling to complete this exercise.

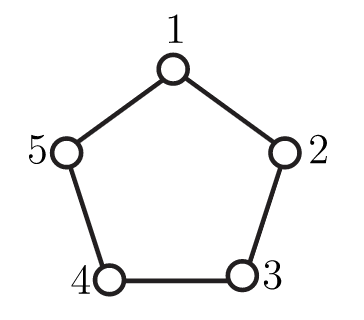
$Screen Shot 2022-03-20 at 5.04.02 PM.png$

Figure 15.15. A pentagon with labeled vertices

a. The dihedral group of the pentagon, $D_{10}$, contains 10 permutations. Let $r_1=(12345)$ be the clockwise rotation by $72^\circ $ and $f_1=(1)(25)(34)$ be the flip about the line passing through 1 and perpendicular to the opposite side. Let $r_2, r_3$, and $r_4$ be the other rotations in $D_{10}$. Denote the flip about the line passing through vertex $i$ and perpendicular to the other side by $f_i$, $1≤i≤5$. Write all 10 elements of $D_{10}$ in cycle notation.

b. Suppose we are coloring the vertices of the pentagon using black and white. Draw the colorings fixed by $r_1$. Draw the colorings fixed by $f_1$.

c. Find $stab_{D_{10}}⁡(C)$ where $C$ is the coloring of the vertices of the pentagon in which vertices 1, 2, and 5 are colored black and vertices 3 and 4 are colored white.

d. Find the cycle index of $D_{10}$.

e. Use the cycle index to determine the number of nonequivalent colorings of vertices of the pentagon using black and white.

f. Making an appropriate substitution for the $x_i$ in the cycle index, find the number of nonequivalent colorings of the vertices of the pentagon in which two vertices are colored black and three vertices are colored white. Draw these colorings.

5. Write all permutations in $C_{12}$, the cyclic group of order 12, in cycle notation.

6. The 12-note western scale is not the only system on which music is based. In classical Thai music, a scale with seven equally-spaced notes per octave is used. As in western music, a scale is a subset of these seven notes, and two scales are equivalent if they are transpositions of each other. Find the number of $k$-note scales in classical Thai music for $1 \leq k \leq 7$.

7. Xylene is an aromatic hydrocarbon having two methyl groups (and four hydrogen atoms) attached to the hexagonal carbon ring. How many isomers are there of xylene?

8. Find the permutations in $S_4^{(2)}$ corresponding to the permutations (1234) and (12)(34) in $S_4$. Confirm that the first consists of a 4-cycle and a 2-cycle and the second consists of two 2-cycles and two 1-cycles.

9. Draw the three nonisomorphic graphs on four vertices with 3 edges and the two nonisomorphic graphs on four vertices with 4 edges.

10.

a. Use the method of Subsection 15.5.3 to find the cycle index of the pair group $S_5^{(2)}$ of the symmetric group on five elements.

b. Use the cycle index from Item 15.6.10.a to determine the number of nonisomorphic graphs on five vertices. How many of them have 6 edges?

11. Tic-tac-toe is a two-player game played on a 9×9 grid. The players mark the squares of the grid with the symbols X and O. This exercise uses Pólya's enumeration theorem to investigate the number of different tic-tac-toe boards. (The analysis of games is more complex, since it requires attention to the order the squares are marked and stopping when one player has won the game.)

$Screen Shot 2022-03-20 at 5.11.23 PM.png$

Figure 15.16. Numbered squares of a tic-tac-toe board

a. Two tic-tac-toe boards are equivalent if one may be obtained from the other by rotating the board or flipping it over. (Imagine that it is drawn on a clear piece of plastic.) Since the 9×9 grid is a square, the group that acts on it in this manner is the dihedral group $D_8$ that we have studied in this chapter. However, as with counting nonisomorphic graphs, we have to be careful to choose the way this group is represented in terms of cycles. Here we are interested in how permutations rearrange the nine squares of the tic-tac-toe board as numbered in Figure 15.16. For example, the effect of the transformation $r_1$, which rotates the board $90^\circ$ clockwise, can be represented as a permutation of the nine squares as (13971)(2684)(5).

Write each of the eight elements of $D_8$ as permutations of the nine squares of a tic-tac-toe board.

b. Find the cycle index of $D_8$ in terms of these permutations.

c. Make an appropriate substitution for $x_i$ in the cycle index to find a generating function $t(X,O)$ in which the coefficient on $X^iO^j$ is the number of nonequivalent tic-tac-toe boards having $i$ squares filled by symbol X and $j$ squares filled by symbol O. (Notice that some squares might be blank!)

d. How many nonequivalent tic-tac-toe boards are there?

e. How many nonequivalent tic-tac-toe boards have three X's and three O's?

f. When playing tic-tac-toe, the players alternate turns, each drawing their symbol in a single unoccupied square during a turn. Assuming the first player marks her squares with X and the second marks his with O, then at each stage of the game there are either the same number of X's and O's or one more X than there are O's. Use this fact and $t(X,O)$ to determine the number of nonequivalent tic-tac-toe boards that can actually be obtained in playing a game, assuming the players continue until the board is full, regardless of whether one of them has won the game.

12. Suppose you are painting the faces of a cube and you have white, gold, and blue paint available. Two painted cubes are equivalent if you can rotate one of them so that all corresponding faces are painted the same color. Determine the number of nonequivalent ways you can paint the faces of the cube as well as the number having two faces of each color.

Hint: It may be helpful to label the faces as U (“up”), D (“down”), F (“front”), B (“back”), L (“left”), and R (“right”) instead of using integers. Working with a three-dimensional model of a cube will also aid in identifying the permutations you require.