2.3: Putting Them Together
( \newcommand{\kernel}{\mathrm{null}\,}\)
When we combine the product rule and the sum rule, we can explore more challenging questions.
Example 2.3.1
Grace is staying at a bed-and-breakfast. In the evening, she is offered a choice of menu items for breakfast in bed, to be delivered the next morning. There are three kinds of items: main dishes, side dishes, and beverages. She is allowed to choose up to one of each, but some of them come with optional extras. From the menu below, how many different breakfasts could she order?
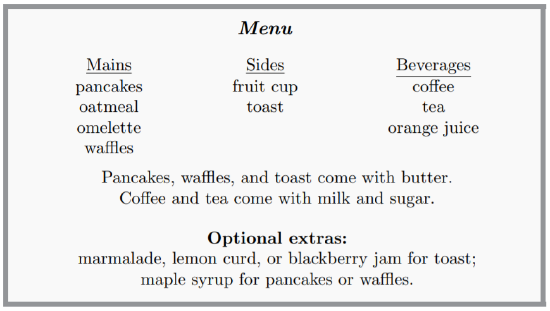
Solution
We see that the number of choices Grace has available depends partly on whether or not she orders an item or items that include optional extras. We will therefore divide our consideration into four cases:
- Grace does not order any pancakes, waffles, or toast.
- Grace orders pancakes or waffles, but does not order toast.
- Grace does not order pancakes or waffles, but does order toast.
- Grace orders toast, and also orders either pancakes or waffles.
In the first case, Grace has three possible choices for her main dish (oatmeal, omelette, or nothing). For each of these, she has two choices for her side dish (fruit cup, or nothing). For each of these, she has four choices for her beverage (coffee, tea, orange juice, or nothing). Using the product rule, we conclude that Grace could order 3·2·4=24 different breakfasts that do not include pancakes, waffles, or toast.
In the second case, Grace has two possible choices for her main dish (pancakes, or waffles). For each of these, she has two choices for her side dish (fruit cup, or nothing). For each of these, she has four choices for her beverage. In addition, for each of her choices of pancakes or waffles, she can choose to have maple syrup, or not (two choices). Using the product rule, we conclude that Grace could order 2·2·4·2=32 different breakfasts that include pancakes or waffles, but not toast.
In the third case, Grace has three possible choices for her main dish (oatmeal, omelette, or nothing). For each of these, she has only one possible side dish (toast), but she has four choices for what to put on her toast (marmalade, lemon curd, blackberry jam, or nothing). For each of these choices, she has four choices of beverage. Using the product rule, we conclude that Grace could order 3·4·4=48 different breakfasts that include toast, but do not include pancakes or waffles.
In the final case, Grace has two possible choices for her main dish (pancakes, or waffles). She has two choices for what to put on her main dish (maple syrup, or only butter). She is having toast, but has four choices for what to put on her toast. Finally, she again has four choices of beverage. Using the product rule, we conclude that Grace could order 2·2·4·4=64 different breakfasts that include toast as well as either pancakes or waffles.
Using the sum rule, we see that the total number of different breakfasts Grace could order is 24+32+48+64=168.
Here’s another example of combining the two rules.
Example 2.3.2
The types of license plates in Alberta that are available to individuals (not corporations or farms) for their cars or motorcycles, fall into one of the following categories:
- vanity plates
- regular car plates
- veteran plates
- motorcycle plates.
None of these license plates use the letters I or O.
Regular car plates have one of two formats: three letters followed by three digits; or three letters followed by four digits (in the latter case, none of the letters A, E, I, O, U, or Y is used).
Veteran plates begin with the letter V, followed by two other letters and two digits. Motorcycle plates have two letters followed by three digits.
Setting aside vanity plates and ignoring the fact that some three-letter words are avoided, how many license plates are available to individuals in Alberta for their cars or motorcycles?
Solution
To answer this question, there is a natural division into four cases: regular car plates with three digits; regular car plates with four digits; veteran plates; and motorcycle plates.
For a regular car plate with three digits, there are 24 choices for the first letter, followed by 24 choices for the second letter, and 24 choices for the third letter. There are 10 choices for the first digit, 10 choices for the second digit, and 10 choices for the third digit. Using the product rule, the total number of license plates in this category is 243⋅103=13,824,000.
For a regular car plate with four digits, there are 20 choices for the first letter, followed by 20 choices for the second letter, and 20 choices for the third letter. There are 10 choices for the first digit, 10 choices for the second digit, 10 choices for the third digit, and 10 choices for the fourth digit. Using the product rule, the total number of license plates in this category is 203⋅104=80,000,000.
For a veteran plate, there are 24 choices for the first letter, followed by 24 choices for the second letter. There are 10 choices for the first digit, and 10 choices for the second digit. Using the product rule, the total number of license plates in this category is 242⋅102=57,600.
Finally, for a motorcycle plate, there are 24 choices for the first letter, followed by 24 choices for the second letter. There are 10 choices for the first digit, 10 choices for the second digit, and 10 choices for the third digit. Using the product rule, the total number of license plates in this category is 242⋅103=576,000.
Using the sum rule, we see that the total number of license plates is
13,824,000+80,000,000+57,600+576,000
which is 94,457,600.
It doesn’t always happen that the sum rule is applied first to break the problem down into cases, followed by the product rule within each case. In some problems, these might occur in the other order. Sometimes there may seem to be one “obvious” way to look at the problem, but often there is more than one equally effective analysis, and different analyses might begin with different rules.
In Example 2.3.1, we could have begun by noticing that no matter what else she may choose, Grace has four possible options for her beverage. Thus, the total number of possible breakfast orders will be four times the number of possible orders of main and side (with optional extras). Then we could have proceeded to analyse the number of possible choices for her main dish and her side dish (together with the extras). Breaking down the choices for her main and side dishes into the same cases as before, we could see that there are 3·2=6 choices in the first case; 2·2·2=8 choices in the second case; 3·4=12 choices in the third case; and 2·2·4=16 choices in the fourth case. Thus she has a total of 6+8+12+16=42 choices for her main and side dishes. The product rule now tells us that she has 4·42=168 possible orders for her breakfast.
Let’s run through one more (simpler) example of using both the sum and product rules, and work out the answer in two different ways.
Example 2.3.3
Kathy plans to buy her Dad a shirt for his birthday. The store she goes to has three different colours of short-sleeved shirts, and six different colours of long-sleeved shirts. They will gift-wrap in her choice of two wrapping papers. Assuming that she wants the shirt gift-wrapped, how many different options does she have for her gift?
Solution
Let’s start by applying the product rule first. There are two aspects that she can vary: the shirt, and the wrapping. She has two choices for the wrapping, so her total number of options will be twice the number of shirt choices that she has. For the shirt, we break her choices down into two cases: if she opts for a short-sleeved shirt then she has three choices (of colour), while if she opts for a long-sleeved shirt then she has six choices. In total she has 3+6=9 choices for the shirt. Using the product rule, we see that she has 2·9=18 options for her gift.
Alternatively, we could apply the sum rule first. We will consider the two cases: that she buys a short-sleeved shirt; or a long-sleeved shirt. If she buys a short-sleeved shirt, then she has three options for the shirt, and for each of these she has two options for the wrapping, making (by the product rule) 3·2=6 options of short-sleeved shirts. If she buys a long-sleeved shirt, then she has six options for the shirt, and for each of these she has two options for the wrapping, making (by the product rule) 6·2=12 options of long-sleeved shirts. Using the sum rule, we see that she has 6+12=18 options for her gift.
Exercise 2.3.1
How many passwords can be created with the following constraints:
- The password is three characters long and contains two lowercase letters and one digit, in some order.
- The password is eight or nine characters long and consists entirely of digits.
- The password is five characters long and consists of lowercase letters and digits. All of the letters must come before all of the digits in the password, but there can be any number of letters (from zero through five).
- The password is four characters long and consists of two characters that can be either digits or one of 16 special characters, and two lowercase letters. The two letters can be in any two of the four positions.
- The password is eight characters long and must include at least one letter and at least one digit.
- The password is eight characters long and cannot include any character more than once.
Exercise 2.3.2
- There are 8 buses a day from Toronto to Ottawa, 20 from Ottawa to Montreal, and 9 buses directly from Toronto to Montreal. Assuming that you do not have to complete the trip in one day (so the departure and arrival times of the buses is not an issue), how many different schedules could you use in travelling by bus from Toronto to Montreal?
- How many 7-bit ternary strings (that is, strings whose only entries are 0, 1, or 2) begin with either 1 or 01


