3.1: Permutations
- Page ID
- 60200
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)We begin by looking at permutations, because these are a straightforward application of the product rule. The word “permutation” means a rearrangement, and this is exactly what a permutation is: an ordering of a number of distinct items in a line. Sometimes even though we have a large number of distinct items, we want to single out a smaller number and arrange those into a line; this is also a sort of permutation.
Definition: Permutation
A permutation of \(n\) distinct objects is an arrangement of those objects into an ordered line. If \(1 ≤ r ≤ n\) (and \(r\) is a natural number) then an r-permutation of \(n\) objects is an arrangement of \(r\) of the \(n\) objects into an ordered line.
So a permutation involves choosing items from a finite population in which every item is uniquely identified, and keeping track of the order in which the items were chosen.
Since we are studying enumeration, it shouldn’t surprise you that what we’ll be asking in this situation is how many permutations there are, in a variety of circumstances. Let’s begin with an example in which we’ll calculate the number of \(3\)-permutations of ten objects (or in this case, people).
Example \(\PageIndex{1}\)
Ten athletes are competing for Olympic medals in women’s speed skating (1000 metres). In how many ways might the medals end up being awarded?
Solution
There are three medals: gold, silver, and bronze, so this question amounts to finding the number of \(3\)-permutations of the ten athletes (the first person in the \(3\)-permutation is the one who gets the gold medal, the second gets the silver, and the third gets the bronze).
To solve this question, we’ll apply the product rule, where the aspects that can vary are the winners of the gold, silver, and bronze medals. We begin by considering how many different athletes might get the gold medal. The answer is that any of the ten athletes might get that medal. No matter which of the athletes gets the gold medal, once that is decided we move our consideration to the silver medal. Since one of the athletes has already been awarded the gold medal, only nine of them remain in contention for the silver medal, so for any choice of athlete who wins gold, the number of choices for who gets the silver medal is nine. Finally, with the gold and silver medalists out of contention for the bronze, there remain eight choices for who might win that medal. Thus, the total number of ways in which the medals might be awarded is \(10 · 9 · 8 = 720\).
We can use the same reasoning to determine a general formula for the number of \(r\)-permutations of \(n\) objects:
Theorem \(\PageIndex{1}\)
The number of \(r\)-permutations of \(n\) objects is \(n(n − 1). . .(n − r + 1)\)
- Proof
-
There are \(n\) ways in which the first object can be chosen (any of the \(n\) objects). For each of these possible choices, there remain \(n-1\) objects to choose for the second object, etc.
Note
We use \(n!\) to denote the number of permutations of \(n\) objects, so
\[n! = n(n − 1). . . 1\].
By convention, we define \(0! = 1\).
Definition: Factorial
We read \(n!\) as “\(n\) factorial,” so \(n\) factorial is \(n(n − 1). . . 1\). Thus, the number of r-permutations of \(n\) objects can be re-written as \(\dfrac{n!}{(n − r)!}\). When \(n = r\) this gives \(\dfrac{n!}{0!} = n!\), making sense of our definition that \(0! = 1\).
Example \(\PageIndex{2}\)
There are 36 people at a workshop. They are seated at six round tables of six people each for lunch. The Morris family (of three) has asked to be seated together (side-by-side). How many different seating arrangements are possible at the Morris family’s table?
Solution
First, there are \(3! = 6\) ways of arranging the order in which the three members of the Morris family sit at the table. Since the tables are round, it doesn’t matter which specific seats they take, only the order in which they sit matters. Once the Morris family is seated, the three remaining chairs are uniquely determined by their positions relative to the Morris family (one to their right, one to their left, and one across from them). There are 33 other people at the conference; we need to choose three of these people and place them in order into the three vacant chairs. There are \(\dfrac{33!}{(33 − 3)!} = \dfrac{33!}{30!}\) ways of doing this. In total, there are \(6 \left( \dfrac{33!}{30!} \right) = 196,416\) different seating arrangements possible at the Morris family’s table.
By adjusting the details of the preceding example, it can require some quite different thought processes to find the answer.
Example \(\PageIndex{3}\)
At the same workshop, there are three round dinner tables, seating twelve people each. The Morris family members (Joy, Dave, and Harmony) still want to sit at the same table, but they have decided to spread out (so no two of them should be side-by-side) to meet more people. How many different seating arrangements are possible at the Morris family’s table now?
Solution
Let’s begin by arbitrarily placing Joy somewhere at the table, and seating everyone else relative to her. This effectively distinguishes the other eleven seats. Next, we’ll consider the nine people who aren’t in Joy’s family, and place them (standing) in an order clockwise around the table from her. There are \(\dfrac{33!}{(33 − 9)!}\) ways to do this. Before we actually assign seats to these nine people, we decide where to slot in Dave and Harmony amongst them.
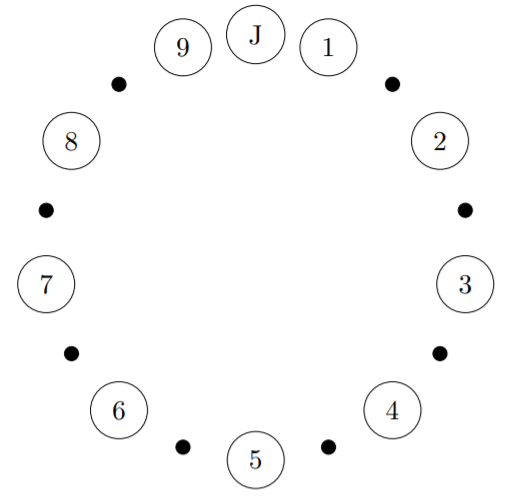
(In the above diagram, the digits \(1\) through \(9\) represent the nine other people who are sitting at the Morris family’s table, and the \(J\) represents Joy’s position.) Dave can sit between any pair of non-Morrises who are standing beside each other; that is, in any of the spots marked by small black dots in the diagram above. Thus, there are eight possible choices for where Dave will sit. Now Harmony can go into any of the remaining seven spots marked by black dots. Once Dave and Harmony are in place, everyone shifts to even out the circle (so the remaining black dots disappear), and takes their seats in the order determined.
We have shown that there are \(\dfrac{33!}{24!} · 8 · 7\) possible seating arrangements at the Morris table. That’s a really big number, and it’s quite acceptable to leave it in this format. However, in case you find another way to work out the problem and want to check your answer, the total number is \(783\), \(732\), \(837\), \(888\), \(000\).
Exercise \(\PageIndex{1}\)
Use what you have learned about permutations to work out the following problems. The sum and/or product rule may also be required.
- Six people, all of whom can play both bass and guitar, are auditioning for a band. There are two spots available: lead guitar, and bass player. In how many ways can the band be completed?
- Your friend Garth tries out for a play. After the auditions, he texts you that he got one of the parts he wanted, and that (including him) nine people tried out for the five roles. You know that there were two parts that interested him. In how many ways might the cast be completed (who gets which role matters)?
- You are creating an \(8\)-character password. You are allowed to use any of the \(26\) lowercase characters, and you must use exactly one digit (from \(0\) through \(9\)) somewhere in the password. You are not allowed to use any character more than once. How many different passwords can you create?
- How many \(3\)-letter “words” (strings of characters, they don’t actually have to be words) can you form from the letters of the word STRONG? How many of those words contain an s? (You may not use a letter more than once.)
- How many permutations of \(\{0, 1, 2, 3, 4, 5, 6\}\) have no adjacent even digits? For example, a permutation like 5034216 is not allowed because \(4\) and \(2\) are adjacent.


