10.2: Inclusion-Exclusion
- Page ID
- 60122
In school, you probably saw Venn diagrams sometimes, showing groups that overlapped with one another. We could draw a very basic Venn diagram showing the kinds of trees that are growing at the various houses on my street:
Looking at the Venn diagram can help us figure out the values of some of the pieces from knowing the values of others. Suppose we know how many houses have deciduous trees, and how many houses have evergreen trees. Naively, you might think that adding these together would give us the total number of houses with trees. However, by looking at the Venn diagram, we see that if we simply add the values together, then any houses that have both kinds of trees have been counted twice (once as a house with a deciduous tree, and again as a house with an evergreen tree). So in order to work out the number of houses that have trees, we can add the number that have deciduous trees to the number that have evergreen trees and then subtract the number that have both kinds of trees. This is the idea of “inclusion-exclusion.”
Specifically, if two sets \(A\) and \(B\) are disjoint, then \(|A ∪ B| = |A|+|B|\). However, if \(A\) and \(B\) are not disjoint, then \(|A| + |B|\) counts the elements of \(A ∩ B\) twice (both as elements of \(A\) and as elements of \(B\)). Subtracting this overcount yields the correct answer:
Proposition \(\PageIndex{1}\): Inclusion-Exclusion For \(2\) Sets
For any finite sets \(A\) and \(B\), we have
\[|A ∪ B| = |A| + |B| − |A ∩ B|\]
- Proof
-
Let \(A_0 = A \setminus B\) and \(B_0 = B \setminus A\), so
- \(A\) is the disjoint union of \(A_0\) and \(A ∩ B\),
- \(B\) is the disjoint union of \(B_0\) and \(A ∩ B\), and
- \(A ∪ B = (A_0 ∪ (A ∩ B)) ∪ (B_0 ∪ (A ∩ B))\) is the disjoint union of \(A_0\), \(B_0\), and \(A ∩ B\).
Then
\[ \begin{equation} \begin{split} |A| + |B| &= (|A_0| + |A ∩ B|) + (|B_0| + |A ∩ B|) \\ &= (|A_0| + |B_0| + |A ∩ B|) + |A ∩ B| \\ &= |A ∪ B| + |A ∩ B| \end{split} \end{equation} \]
Example \(\PageIndex{1}\)
Let \(A = \{p,r, o, n, g\}\) and \(B = \{h, o,r, n,s\}\). Then,
\(|A| = 5\), \(|B| = 5\), and \(|A ∩ B| = |\{r, o, n\}| = 3\),
so Inclusion-Exclusion tells us that
\(|A ∪ B| = |A| + |B| − |A ∩ B| = 5 + 5 − 3 = 7\)
This is correct, since
\(|A ∪ B| = |\{p,r, o, n, g, h,s\}| = 7\).
Example \(\PageIndex{2}\)
Every one of the \(4000\) students at Modern U owns either a tablet or a smartwatch (or both). Surveys show that:
- \(3500\) students own a tablet, and
- \(1000\) students own a smartwatch.
How many students own both a tablet and a smartwatch?
Solution
Let
- \(S\) be the set of all students at Modern U,
- \(T\) be the set of students who own a tablet, and
- \(W\) be the set of students who own a smart watch.
Then, by assumption,
\(|S| = 4000\), \(|T| = 3500\), \(|W| = 1000\).
Since every student owns either a tablet or a smartwatch, we have \(S = T ∪ W\). Therefore, Inclusion-Exclusion tells us that
\(|S| = |T ∪ W| = |T| + |W| − |T ∩ W|\),
so
\(|T ∩ W| = |T| + |W| − |S| = 3500 + 1000 − 4000 = 500\).
Hence, there are exactly \(500\) students who own both a tablet and a smart watch.
The following exercise provides a formula for the union of three sets \(A\), \(B\), and \(C\). The idea is that \(A ∩ B\), \(A ∩ C\), and \(B ∩ C\) have all been overcounted. However, subtracting all of these will overcompensate, because the elements of \(A ∩ B ∩ C\) have been subtracted too many times, so they need to be added back in.
Exercise \(\PageIndex{1}\)
Suppose \(A\), \(B\), and \(C\) are finite sets. Show
\(|A ∪ B ∪ C| = |A| + |B| + |C| − |A ∩ B| − |A ∩ C| − |B ∩ C| + |A ∩ B ∩ C|\).
[Hint: We have formulas for \(|(A ∪ B) ∪ C|\) and \(|A ∪ B|\). The equality \((A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)\) provides another useful formula.
The following general formula calculates the cardinality of the union of any number of sets, by adding or subtracting the cardinality of every possible intersection of the sets. It is called the Inclusion-Exclusion formula, because it works by adding (or “including”) the cardinalities of certain sets, and subtracting (or “excluding”) the cardinalities of certain other sets.
Theorem \(\PageIndex{1}\): Inclusion-Exclusion
Let \(A_1, . . . , A_n\) be finite sets. Then
\[|A_1 ∪ . . . ∪ A_n| = \left( \sum_{i=1}^{n} |A_i| \right) - \left( \sum_{1≤i<j≤n}^{n} |A_i ∩ A_j | \right) + ... + ((−1)^{n+1} |A_1 ∩ . . . ∩ A_n|) \]
Of course, we can figure out the value of any one of the terms in the inclusion-exclusion formula, if we know the values of all of the other terms
Example \(\PageIndex{3}\)
Sandy’s class is at Calaway Park. There are \(21\) students in the class. At the end of the day, the teacher asks some questions and determines the following:
- Every student rode at least one of the roller coaster, the train, the log ride, or the bumper cars;
- \(13\) students rode the roller coaster;
- \(6\) students rode the train;
- \(12\) students rode the log ride;
- \(15\) students rode the bumper cars;
- \(2\) students rode all four of the rides; and
- \(10\) students rode at least \(3\) of these \(4\) rides.
How many students rode exactly two of the four rides?
Solution
We begin by establishing some notation. Let \(A_1\) be the set of students who rode the roller coaster; \(A_2\) will be the set of students who rode the train; \(A_3\) will be the set of students who rode the log ride; and \(A_4\) will be the set of students who rode the bumper cars.
Ignoring the last piece of information for a moment, the rest of we have been given tells us that:
- \(|A_1 ∪ A_2 ∪ A_3 ∪ A_4| = 21\);
- \(|A_1| = 13\);
- \(|A_2| = 6\);
- \(|A_3| = 12\);
- \(|A_4| = 15\); and
- \(|A_1 ∩ A_2 ∩ A_3 ∩ A_4| = 2\).
The last piece of information is a bit more tricky to encode. Observe that if we take \(|A_1 ∩A_2 ∩A_3|+|A_1 ∩A_2 ∩A_4|+|A_1 ∩A_3 ∩A_4|+|A_2 ∩A_3 ∩A_4|\), using ideas similar to inclusion-exclusion (or drawing the Venn diagram) we see that we have found the number of students who rode at least \(3\) of the \(4\) rides, except that we have counted the number of students who rode all \(4\) rides in each of the four summands, instead of counting it only once. So we need to subtract \(|A_1 ∩ A_2 ∩ A_3 ∩ A_4|\) off three times to get the number of students who rode at least \(3\) of the \(4\) rides. Since we know that \(|A_1 ∩ A_2 ∩ A_3 ∩ A_4| = 2\), this tells us that
\(|A_1 ∩ A_2 ∩ A_3| + |A_1 ∩ A_2 ∩ A_4| + |A_1 ∩ A_3 ∩ A_4| + |A_2 ∩ A_3 ∩ A_4| − 6 = 10\),
so
\(|A_1 ∩ A_2 ∩ A_3| + |A_1 ∩ A_2 ∩ A_4| + |A_1 ∩ A_3 ∩ A_4| + |A_2 ∩ A_3 ∩ A_4| = 16\).
Thus, the inclusion-exclusion formula tells us that
\(21 = (13 + 6 + 12 + 15) − \sum_{1≤i<j≤4} | A_i ∩ A_j | + 16 − 2\),
so \(\sum_{1≤i<j≤4} |A_i ∩ A_j | = 39\). Unfortunately, this still isn’t quite what we’re looking for. The value we want is the number of students who rode exactly two of the four rides. Again, similar reasoning shows that the number of students who rode the roller coaster and the train but neither of the other two rides, will be given by:
\(|A_1 ∩ A_2| − |A_1 ∩ A_2 ∩ A_3| − |A_1 ∩ A_2 ∩ A_4| + |A_1 ∩ A_2 ∩ A_3 ∩ A_4|\).
Similar formulas can be worked out for each of the other five pairs that can be formed from the four rides. What we have been asked for, is the sum of these six formulas. This works out to
\( \sum_{1≤i<j≤4} |A_i ∩ A_j | - 3 \left( \sum_{1≤i<j<k≤4} |A_i ∩ A_j ∩ A_k| \right) + 6|A_1 ∩A_2 ∩A_3 ∩A_4| = 39−3(16)+ 6(2) = 3 \).
Only three of the students rode exactly two of the four rides.
This was a very complicated example. You should not expect to have to work out examples that are quite so tricky, but this gives you an idea of the power of inclusion-exclusion. Here is a more straightforward application.
Example \(\PageIndex{4}\)
In the Faculty of Arts and Science, the voting method used is “approval;” that is, regardless of the number of positions available, each voter can mark as many boxes as they wish on their ballot.
Imagine that Prof. Li, Prof. Cheng, and Prof. Osborn were all nominated for two computer science positions on the department’s search committee. Barb Hodgson notes the following facts when counting the ballots:
- Prof. Cheng received \(18\) votes; Prof. Osborn received \(15\) votes, and Prof. Li received 10 votes.
- Only one ballot had all three boxes marked.
- Five of the ballots were marked for both Prof. Osborn and Prof. Li.
- Ten of the ballots were marked for Prof. Cheng and Prof. Osborn.
- Six of the ballots were marked for Prof. Cheng and Prof. Li.
How many members of the department voted in the election?
Solution
Again, we begin by establishing some notation. Let \(C\) be the set of ballots that were marked for Prof. Cheng; let \(O\) be the set of ballots that were marked for Prof. Osborn; and let \(L\) be the set of ballots that were marked for Prof. Li. Then what we want is \(|C ∪ O ∪ L|\): the number of ballots that were marked for at least one of the three candidates; this is the same as the number of people who voted.
Inclusion-Exclusion tells us that
\(|C ∪ O ∪ L| = |C| + |O| + |L| − |C ∩ O| − |C ∩ L| − |O ∩ L| + |C ∩ O ∩ L|\).
We have been given all of the values on the right-hand side of this equation, so we see that
\(|C ∪ O ∪ L| = 18 + 15 + 10 − 10 − 6 − 5 + 1 = 23\).
There were \(23\) department members who voted in the election.
In fact, the information we have been given is enough for us to fill in the values in every piece of the Venn diagram.
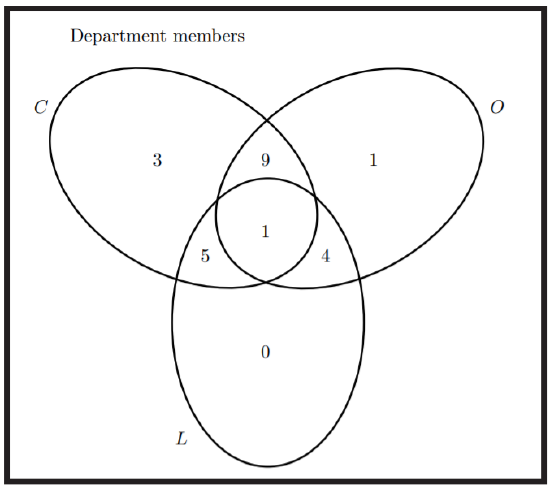
The \(9\) people who voted for Prof. Cheng and Prof. Osborn but not Prof. Li is determined from the fact that \(10\) people voted for Professors Cheng and Osborn, and only one of those voted for all three professors. Similarly, the \(4\) people who voted for Prof. Li and Prof. Osborn but not Prof. Cheng is determined from the fact that \(5\) people voted for Professors Li and Osborn, and only one of those voted for all three professors; also, the \(5\) people who voted for Prof. Cheng and Prof. Li but not Prof. Osborn is determined from the fact that \(6\) people voted for Professors Cheng and Li, and only one of those voted for all three professors.
From the above deductions, we see that of the \(18\) votes Prof. Cheng received, one ballot was marked for all \(3\) candidates; \(9\) were marked for Professors Cheng and Osborn (but not Li); and \(5\) were marked for Professors Cheng and Li (but not Osborn). The remaining \(3\) votes must have been for Prof. Cheng alone, allowing us to fill in that spot. Similarly, of the \(15\) votes Prof. Osborn received, one ballot was marked for all \(3\) candidates; \(9\) were marked for Professors Cheng and Osborn (but not Li); and \(4\) were marked for Professors Osborn and Li (but not Cheng). The remaining vote must have been for Prof. Osborn alone, allowing us to fill in that spot. Finally, all of Prof. Li’s \(10\) votes are accounted for between the \(5\) who voted for Professors Cheng and Li (but not Osborn), the \(4\) who voted for Professors Li and Osborn (but not Cheng) and the one who voted for all three, so we put a \(0\) into the final spot.
Exercise \(\PageIndex{2}\)
- Of \(15\) students in a stats class, \(8\) are math majors, \(6\) are CS majors, and \(7\) are in education. None are in all three, and none have any other majors. There are two math/CS joint majors, and \(3\) CS majors who are in education. How many math majors are in education? How many of the math majors are not in either CS or education?
- Kevin has \(165\) apps on his phone. Every one of these that is not a game and was not free, requires internet access. Of these, \(78\) were free. Internet access is necessary for \(124\) of the apps to function fully. Of the apps on his phone, \(101\) are games. Kevin has \(62\) games on his phone that require internet access; \(48\) of these were free. Out of all of the games on his phone, \(58\) were free. How many of the free apps on Kevin’s phone that aren’t games, require internet access?
- How many integers between \(1\) and \(60\) are divisible by at least one of \(2\), \(3\), and \(5\)?
- In the \(403\) area code, how many of the \(10\)-digit possible phone numbers (where any combination of digits is allowed) contain at least one of each odd digit?
- Assume \(|U| = 15\), \(|V | = 12\), and \(|U ∩ V | = 4\). Find \(|U ∪ V |\).
- Assume \(|R| = 13\), \(|S| = 17\), and \(|R ∪ S| = 25\). Find \(|R ∩ S|\).
- Assume \(|J| = 300\), \(|J ∪ L| = 500\), and \(|J ∩ L| = 150\). Find \(|L|\).
- At a small university, there are \(90\) students that are taking either Calculus or Linear Algebra (or both). If the Calculus class has \(70\) students, and the Linear Algebra class has \(35\) students, then how many students are taking both Calculus and Linear Algebra?
- How many numbers from \(1\) to \(5000\) are divisible by either \(3\) or \(17\)?
- How many \(12\)-digit numbers (in which the first digit is not \(0\)) have either no \(0\) or no \(5\)?


