16.3: Systems of Distinct Representatives

Suppose we start filling in a Latin square, one row at a time, at each step ensuring that no element has yet appeared more than once in a column (or in a row). Under what conditions will it be impossible to complete this to a Latin square? Although it may not be immediately obvious, the answer to this question can be found in a well-known theorem published by Philip Hall in \(1935\), about systems of distinct representatives.

Definition: Word

Let \(T_1 . . . , T_n\) be sets. If there exist \(a_1, . . . , a_n\) all distinct such that for every \(1 ≤ i ≤ n\), \(a_i ∈ T_i\), then \(\{a_1, . . . a_n\}\) form a system of distinct representatives (SDR) for \(T_1, . . . , T_n\).

Example \(\PageIndex{1}\)

The university is striking a student committee on the subject of tutorials. For each of the \(5\) Faculties, they ask students to elect one representative who is taking classes from that faculty. They do not want one student trying to represent more than one faculty. The candidates are:

• Joseph, who is taking courses in Arts and Science, Fine Arts, Management, and Education;
• René, who is taking courses in Health Sciences;
• Claire, who is taking courses in Education and Health Sciences;
• Sandra, who is taking courses in Management, Fine Arts, and Health Sciences;
• Laci, who is taking courses in Education and Health Sciences; and
• Jing, who is taking courses in Education.

Can the committee be filled?

Solution

The answer is no. For the three Faculties of Arts & Science, Fine Arts, and Management, there are only two possible student representatives: Joseph (who could represent any of the three), and Sandra (who could represent either Fine Arts or Management). So it is not possible to elect one student to represent each of the five Faculties, without allowing one of these students to fill two roles.

In Example 16.3.1, we observed that we could find a collection of the sets to be represented, that collectively had fewer possible representatives than there are sets in the collection. It is easy to see that if this happens, there cannot be a system of distinct representatives for the sets.

What Philip Hall proved is the converse: unless we have an obstruction of this type, it is always possible to fine a system of distinct representatives.

Theorem \(\PageIndex{1}\): Hall's Theorem

The collection of sets \(T_1, . . . , T_n\) has a system of distinct representatives if and only if for every \(1 ≤ k ≤ n\), the union of any \(k\) of the sets has cardinality at least \(k\).

This theorem is often referred to as “Hall’s Marriage Theorem,” as one of the problems it solves can be stated as follows. Suppose we have a collection of men and a collection of women. Each of the women has a list of men she likes (from the collection). When is it possible to marry each of the women to a man that she likes? (The context is historical, and the assumption of the time was that every woman would want to marry a man.)

We have seen that one of the two implications of Hall’s Theorem is easy to prove. We will not try to prove the other implication here, but will focus on using the result. Here are some examples and exercises. For completeness, we provide a proof of Hall’s Theorem at the end of this chapter.

Example \(\PageIndex{2}\)

Let \(A_1 = \{a, b, c, d\}\), \(A_2 = \{b, c\}\), \(A_3 = \{b\}\), \(A_4 = \{b, c\}\). Does this collection of sets have a system of distinct representatives? If so, find one; if not, explain why.

Solution

The answer is that this collection of sets has no system of distinct representatives, because the union of three sets \(A_2\), \(A_3\), and \(A_4\) has only two elements: \(b\) and \(c\).

Example \(\PageIndex{3}\)

Let \(A_1 = \{a, d\}\), \(A_2 = \{a, c\}\), \(A_3 = \{b, c\}\), \(A_4 = \{c, d\}\). Does this collection of sets have a system of distinct representatives? If so, find one; if not, explain why.

Solution

This collection of sets does have a system of distinct representatives: take \(a\) for \(A_1\), \(c\) for \(A_2\), \(b\) for \(A_3\), and \(d\) for \(A_4\). For clarity, we underline the representatives in the following list of the sets: \(A_1 = \{\underline{a}, d\}\), \(A_2 = \{a, \underline{c}\}\), \(A_3 = \{\underline{b}, c\}\), \(A_4 = \{c, \underline{d}\}\).

(In fact, it also has another system of distinct representatives: take \(d\) for \(A_1\), \(a\) for \(A_2\), \(b\) for \(A_3\), and \(c\) for \(A_4\): \(A_1 = \{a, \underline{d}\}\), \(A_2 = \{\underline{a}, c\}\), \(A_3 = \{\underline{b}, c\}\), \(A_4 = \{\underline{c}, d\}\). )

Exercise \(\PageIndex{1}\)

For each collection of sets, determine whether or not it has a system of distinct representatives. If so, find one; if not, explain why.

1) \(A_1 = \{x\}\), \(A_2 = \{y, z\}\), \(A_3 = \{x, y\}\).

2) \(A_1 = \{u, v, w, x, y, z\}\), \(A_2 = \{v, w, y\}\), \(A_3 = \{w, x, y\}\), \(A_4 = \{v, w, x, y\}\), \(A_5 = \{v, x, y\}\), \(A_6 = \{v, y\}\).

3) \(A_1 = \{x\}\), \(A_2 = \{y\}\), \(A_3 = ∅\).

4) \(A_1 = \{x, z\}\), \(A_2 = \{y\}\), \(A_3 = \{x, y, z\}\).

5) \(T_1 = \{a, b, c, d\}\), \(T_2 = \{a, b, c\}\), \(T_3 = \{a\}\), \(T_4 = \{c\}\).

6) \(U_1 = \{x, y\}\), \(U_2 = \{y, z\}\), \(U_3 = ∅\).

7) \(V_1 = \{e, f\}\), \(V_2 = \{e, g\}\), \(V_3 = \{e, h\}\), \(V_4 = \{f, g\}\), \(V_5 = \{h, i\}\).

8) \(W_1 = \{+, −, ×, ÷, 0\}\), \(W_2 = \{+, −, ×\}\), \(W_3 = \{+, ×\}\), \(W_4 = \{×, −\}\), \(W_5 = \{+, −\}\).

Let’s return to our original question about Latin squares. To answer this, we first give an important general consequence of Hall’s Theorem.

Proposition \(\PageIndex{1}\)

Suppose \(T_1, . . . , T_n\) is a collection of sets each of which contains exactly \(r\) elements. Further, suppose that no element appears in more than \(r\) of the sets. Then this collection has a system of distinct representatives.

Proof

By Hall’s Theorem, we must show that for every \(1 ≤ k ≤ n\), the union of any \(k\) of the sets \(T_1, . . . , T_n\) has cardinality at least \(k\). Let \(k ∈ {1, . . . , n}\) be arbitrary, and arbitrarily choose \(k\) of the sets \(T_{j_1}, . . ., T_{j_k}\). If \(k ≤ r\) then since each \(T_{j_i}\) has \(r\) elements, their union must have at least \(r ≥ k\) elements, as desired.

Suppose on the other hand that \(k > r\). Amongst the \(k\) sets of \(r\) elements, a total of \(kr\) elements appear (counting each element every time it appears). Since each element appears in at most \(r\) of the sets, it must be the case that at least \(k\) distinct elements appear. This completes the proof.

We can now answer the question about Latin squares.

Theorem \(\PageIndex{2}\)

Suppose that \(m\) rows of a Latin square of order \(n\) have been filled, where \(m < n\), and that to this point no entry appears more than once in any row or column. Then another row can be added to the Latin square, maintaining the condition that no entry appears more than once in any row or column.

Proof

For \(1 ≤ i ≤ n\), let \(T_i\) be the set of elements that have not yet appeared in column \(i\) (from the entries in the first \(m\) rows). So \(T_i\) can be thought of as the set of allowable entries for the \(i^{\text{th}}\) column of the new row. Notice that each \(T_i\) has cardinality \(n − m\) (the number of rows that are still empty). The task of finding a new row all of whose entries are distinct, and whose \(i^{\text{th}}\) entry comes from the set \(T_i\) of allowable entries for that column, is equivalent to finding a system of distinct representatives for the sets \(T_1, . . . , T_n\). Thus, we must show that the collection \(T_1, . . . , T_n\) has a system of distinct representatives.

Notice also that every element has appeared once in each of the first \(m\) rows, and thus has appeared in precisely \(m\) of the columns. Therefore, there are exactly \(n − m\) of the columns in which it has not yet appeared. In other words, each element appears in exactly \(n − m\) of the sets.

We can now apply Proposition 16.3.1, with \(r = n − m\) to see that our sets do have a system of distinct representatives. This can be used to form a new row for the Latin square.

Corollary \(\PageIndex{1}\)

Suppose that \(m\) rows of a Latin square of order \(n\) have been filled, where \(m < n\), and that to this point no entry appears more than once in any row or column. This structure can always be completed to a Latin square.

Proof

As long as \(m < n\), we can repeatedly apply Theorem 16.3.2 to deduce that it is possible to add a row. Once you actually find a row that can be added (note that the statement of Hall’s Theorem does not explain how to do this), do so. Eventually, this process will result in a complete square.

Hall’s Theorem can also be used to prove a special case of a result we proved previously, Theorem 14.1.3. The special case we can prove with Hall’s Theorem, is the case where every vertex has the same valency.

Theorem \(\PageIndex{3}\)

If \(G\) is a bipartite graph in which every vertex has the same valency, then any bipartition sets \(V_1\) and \(V_2\) have the same cardinality, and there is a set of \(|V_1|\) edges that can be properly coloured with the same colour.

Proof

Let \(k\) be the valency of every vertex, and for some arbitrary bipartition sets \(V_1\) and \(V_2\), let \(n = |V_1|\). By a slight adaptation of Euler’s handshaking lemma, taking into account the fact that every edge has exactly one of its endvertices in \(V_1\), we see that \(nk = |E|\). By the same argument, \(k|V_2| = |E|\), which forces \(|V_2| = n = |V_1|\). Since the bipartition was arbitrary, the first statement follows.

Let \(V_1 = \{v_1, . . . , v_n\}\). For every \(1 ≤ i ≤ n\), let

\[T_i = \{u ∈ V | u ∼ v_i\}.\]

A system of distinct representatives for the sets \(T_1, . . . , T_n\) will produce \(n = |V_1|\) edges that can be properly coloured with the same colour.

Observe that every set \(T_i\) has cardinality \(k\) (since this is the valency of every vertex), and every vertex appears in exactly \(k\) of the sets (again because this is the valency of the vertex). Therefore, by Proposition 16.3.1, there is a system of distinct representatives for \(T_1, . . . , T_n\). Hence we can find \(n = |V_1|\) edges that can be properly coloured with the same colour.

Corollary \(\PageIndex{2}\)

If \(G\) is a bipartite graph in which every vertex has the same valency \(k\), then its edges can be properly coloured using \(k\) colours.

Proof

Repeat the following step \(k\) times: find a set of edges that can be properly coloured. Colour them with a new colour, and delete them from the graph.

At each stage, Theorem 16.3.3 tells us providing that every vertex has the same valency, we can find a set of edges that are properly coloured, one of which is incident with every vertex of the graph. Since the valency of every vertex is reduced by exactly one when we delete such a set of edges, at each stage every vertex will have the same valency.

To conclude the chapter, we provide a proof of Hall’s Theorem. As previously noted, one direction is obvious, so we prove only the other direction.

Theorem \(\PageIndex{4}\): Hall's Theorem

The collection of sets \(T_1, . . . , T_n\) has a system of distinct representatives if for every \(1 ≤ k ≤ n\), the union of any \(k\) of the sets has cardinality at least \(k\).

Proof

We will prove this by strong induction on the number of sets, \(n\).

Base case: \(n = 1\). If a single set has one element, then that set has a representative. This completes the proof of the base case.

Inductive step: We begin with the inductive hypothesis. Let \(m ≥ 1\) be arbitrary. Suppose that whenever \(1 ≤ i ≤ m\), and a collection of \(i\) sets \(T_1, . . . , T_i\) has the property that for every \(1 ≤ k ≤ i\), the union of any \(k\) of the sets has cardinality at least \(k\), then that collection of sets has a system of distinct representatives.

We want to deduce that whenever we have a collection of \(m + 1\) sets with the property that for every \(1 ≤ k ≤ m + 1\), the union of any \(k\) of the sets has cardinality at least \(k\), then that collection of sets has a system of distinct representatives. Let \(T_1, . . . , T_{m+1}\) be such a collection of sets.

We look at the subcollection of sets \(T_1, . . . , T_m\), and consider two cases. First, suppose that for every \(1 ≤ k ≤ m\), the union of any \(k\) of these sets has cardinality at least \(k + 1\). In this case, take any element \(t ∈ T_{m+1}\) (which by hypothesis is nonempty) to be the representative for \(T_{m+1}\), and remove this element from each of the other sets. Due to the case we are in, for every \(1 ≤ k ≤ m\), the union of any \(k\) of the sets \(T_1 − \{t\}, . . . , T_m − \{t\}\) still has cardinality at least \(k\), (we have removed only the element \(t\) from this union, which previously had cardinality at least \(k + 1\)). Thus we can apply our induction hypothesis to find a system of distinct representatives for \(T_1, . . . , T_m\) that does not include the element \(t\). This completes a system of distinct representatives for our full collection of sets.

The other case is that there is some \(1 ≤ k ≤ m\) and some collection of \(k\) of the sets \(T_1, . . . , T_m\), whose union has cardinality precisely \(k\). By our induction hypothesis, there is a system of distinct representatives for these \(k\) sets. From the other \(m + 1 − k\) sets (observe that \(1 ≤ m + 1 − k ≤ m\)), remove the \(k\) elements that were in the union of the original \(k\) sets. Consider any \(k'\) of these adjusted sets, with \(1 ≤ k' ≤ m + 1 − k\). Observe that the union of the \(k + k'\) sets consisting of the original \(k\) sets together with these \(k'\) sets must have contained at least \(k + k'\) distinct elements by hypothesis, so after removing the \(k\) representatives of the original \(k\) sets (which are the only elements in those sets), these \(k'\) sets must still have at least \(k'\) distinct elements in their union. Therefore, we can apply our induction hypothesis to these other \(m + 1 − k\) adjusted sets, and see that they too have a system of distinct representatives, none of which are amongst the \(k\) representatives for the original \(k\) sets. Combining these two systems of distinct representatives yields a system of distinct representatives for the full collection of sets.

Exercise \(\PageIndex{2}\)

1) Onyx is doing some research on what people learn from visiting different countries. She has a set of questions that are to be answered by someone who has visited the country. Before fully launching the study, she wants to try the questions out on some of her friends. Since the questions are the same for different countries, she doesn’t want one person to answer the questions for more than one country, as that could bias the results. Of her close friends, the following people have visited the following countries:

• England: Adam, Ella, Justin
• Wales: Adam, Justin, Faith, Cayla
• Scotland: Bryant, Justin, Ella
• Ireland: Adam, Bryant, Justin
• Germany: Cayla, Bryant, Justin, Faith, Denise
• France: Ella, Justin, Bryant
• Italy: Adam, Ella, Bryant

Prove that Onyx cannot find seven different friends, each of whom has visited a different one of these countries.

2) Can the following be completed to a \(4 \times 4\) Latin square? Does Hall’s Theorem apply to this? If not, why not?

\( 1\; \; 2\; \; 3\; \; 4 \\ 4\; \; 1\; \; 2\; \; 3 \\ 2\; \; 4\; \;\;\;\;\;\;\;\\ \)

3) Show (by example) that it is possible to have a bipartite graph in which the bipartition sets have the same cardinality \(k\) and the valency of every vertex is either \(3\) or \(4\), but no set of \(k\) edges can be properly coloured with a single colour.

4) How do you know (without actually finding a completion) that the following can be completed to a Latin square of order \(7\)?

\( 1\; \; 2\; \; 3\; \; 4\;\;5\;\;6\;\;7 \\ 2\; \; 4\; \; 7\; \; 6\;\;1\;\;5\;\;3 \\ 3\; \; 7\; \; 4\; \; 2\;\;6\;\;1\;\;5 \\ 4\; \; 6\; \; 2\; \; 5\;\;3\;\;7\;\;1 \\ \)

5) Find a completion of the partial Latin square in Problem \(4\).

6) For each of these bipartite graphs, let \(V_1 = \{a, b, c, d, e, f\}\), and determine whether there is a set of \(|V_1|\) disjoint edges. (In other words, determine whether there is a set of \(|V_1|\) edges that can be properly coloured with the same colour.)

(a)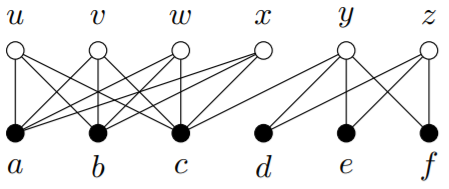

(b)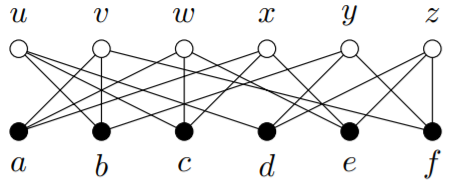

(c)