Appendix A: Solutions To Selected Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
For the reader’s convenience, solutions below are given with full work shown as well as a final numerical solution. Typically the final numerical solution would not be expected, but makes it easier to verify an answer that has been reached using a different method.
Solutions for Chapter 2
Solutions to Exercise 2.1.1
1) There are 4 choices for colour; 2 choices for air conditioning; 5 choices for stereo; and 3 choices for floor mats. So in total, there are 4 · 2 · 5 · 3 = 120 different combinations of options. Of these, 3 combinations are available at the dealership, so the probability that one of these cars has the options he wants is \dfrac{3}{120} = \dfrac{1}{40}.
2) In Candyce’s book, the reader will have 3 choices at the first decision point, and 2 choices at each of the following three decision points. Thus, there are a total of 3 · 2 · 2 · 2 = 3 · 2^3 = 24 possible storylines. Candyce must write 24 endings.
Solutions to Exercise 2.2.1
1) Let’s call the black markers Black A, Black B, and Black C. The four possible options are: I leave behind the blue marker; I leave behind Black A; I leave behind Black B; I leave behind Black C. In each of the final three cases, I take the blue marker. Therefore, the probability that I take the blue marker is \dfrac{(1 + 1 + 1)}{4} = \dfrac{3}{4}.
2) If Maple is thinking of a letter, there are 26 things she could be thinking of. If she is thinking of a digit, there are 10 things she could be thinking of. In total, there are 10 + 26 = 36 things she could be thinking of.
Solutions to Exercise 2.3.1
1) We divide the possible passwords into three cases, depending on whether the digit is in the first, second, or third position. In each case, we have 10 choices for the digit, 26 choices for the first lowercase letter, and 26 choices for the second lowercase letter. Thus, in each case, we have 10 · 262 possible passwords. In total, there are 10·262+10·262+10·262 = 30·262 = 20280 different passwords with these constraints.
2) We divide the possible passwords into two cases, depending on whether there are 8 or 9 characters. If there are 8 characters, then the product rule tells us that there are 10^8 passwords consisting entirely of digits (10 choices for the digit in each of the 8 positions). Similarly, if there are 9 characters, then there are 10^9 passwords consisting entirely of digits. In total, there are 10^8 + 10^9 = 1,100,000,000 passwords with these constraints.
Solutions to Exercise 2.4.1
It is sometimes possible to turn a use of the sum rule into a use of the product rule, or vice versa, so you might get different answers that could be correct. The answers below represent one natural way of solving each problem.
1) Use both rules. There are two cases that should be added together: the number of numbers that have two digits, and the number of numbers that have four digits. For each of these cases, use the product rule to determine how many numbers have this property. (The answer is 9 · 10 + 9 · 10^3 = 9090. Note that in order for a number to have exactly k digits, the leading digit cannot be zero.)
2) Use only the product rule. There are 6 outcomes from the red die, and for each of these, there are 6 outcomes from the yellow die, for a total of 6 · 6 = 36 outcomes.
Solutions for Chapter 3
Solutions to Exercise 3.1.1
1) The band may choose any one of the 6 people to play lead guitar. They may then choose any one of the remaining 5 people to play bass. Therefore, the band can be completed in 6 · 5 = 30 ways. You might also observe that the number of ways to complete the band is the number of 2-permutations (for the two open spots) of 6 people, which is 6 · . . . · (6 − 2 + 1) = 6 · 5 = 30.
2) Divide this into two cases, depending on which of the two parts Garth got. If he got the first part, then there were 8 other people competing for 4 other roles, so the number of ways of completing the cast in this case is the number of 4-permutations of the 8 people. Repeating this argument for the second case (if Garth got the other part) and adding the two numbers, we see that in total there are 2 · 8 · 7 · 6 · 5 (since 8−4 + 1 = 5) ways of completing the cast. This works out to 3360.
Solutions to Exercise 3.2.1
2) At the end of this trick, the only sets of cards that she could not possibly end up with are sets that contain nothing but spades. There are \binom{13}{3} sets that include only spades (choose any 3 of the 13 spades), and \binom{52}{3} possible sets of 3 cards from the deck as a whole, so the number of sets of three cards that are not all spades is \binom{52}{3} − \binom{13}{3} = 22100 − 286 = 21814.
3) The leading digit cannot be a zero, so if there are to be exactly two zeroes, we have 4 possible positions in which they can be placed. Thus, there are \binom{4}{2} ways of choosing where to place the two zeroes. In each of the remaining three positions, we can place any of the digits 1 through 9, so there are 93 choices for the remaining digits. Thus, there are \binom{4}{2} \dfrac{9}{3} = 4374 5-digit numbers that contain exactly two zeroes.
Solutions to Exercise 3.3.1
2) Using the Binomial Theorem, we see that
(a + b)^5 (c + d)^6 = \left( \sum_{r=0}^{5} \binom{5}{r} a^rb^{5-r} \right) \left( \sum_{s=0}^{6} \binom{6}{s} c^sd^{6-s} \right) .
To find the coefficient of a^2 b^3 c^2 d^4, we must take r = 2 and s = 2. This gives us the term \binom{5}{2} a^2 b^3 \binom{6}{2} c^2 d^4 = \binom{5}{2} \binom{6}{2} a^2 b^3 c^2 d^4. Thus, the coefficient of a^2 b^3 c^2 d^4 is \binom{5}{2} \binom{6}{2} = 10 · 15 = 150.
4) Using the Binomial Theorem, we see that
(a + b)^5 (c + d)^6 = \sum_{r=0}^{5} \binom{5}{r} a^rb^{5-r} + \sum_{s=0}^{4} \binom{4}{s} c^sd^{4-s} .
The coefficient of a^3 b^2 in the first summand arises when r = 3; in the second summand, it arises when s = 3. This gives us the term \binom{5}{3} a^3 b^2 + \binom{4}{3} a^3 (b^2)^1. Thus, the coefficient of a^3 b^2 is \binom{5}{3} + \binom{4}{3} = 10 + 4 = 14.
Solutions for Chapter 4
Solutions to Exercise 4.1.3
1) When counting the number of subsets of an n-set, we saw that there is a bijection between that number and the number of binary strings of length n: identify each element of the set with a position in the string, and put a 0 in that position if the element is not in the subset, and a 1 if it is. Analogously, we can find a bijection between the number of these structures and the number of ternary strings of length n (strings containing 0, 1, or 2 in each position). Identify each element of the set with a position in the string, put a 0 in that position if the element is not in the structure, a 1 if it occurs once, and a 2 if it occurs twice. Thus, we can form 3n structures from the set \{1, . . . , n\}: there are 3 choices for each of the n entries in the ternary string.
3) We identify each of the ten Olympic contenders with a crib, and each of the three dolls with one of the three medals. If the doll corresponding to the gold medal goes into crib i, this corresponds to the competitor corresponding to crib i winning the gold medal. Similarly, if the doll corresponding to the silver medal goes into crib j, this is equivalent to the contender corresponding to crib j winning the silver medal; and the doll corresponding to bronze going into crib k is equivalent to the contender corresponding to crib k winning the bronze medal.
Solutions to Exercise 4.2.2
2) COMBINATORIAL PROOF. We use the problem given to us in the hint, so will be counting the number of ways to start with n dogs, determine r who will enter a competition and k of those who will be finalists.
Counting Method 1
From the n dogs, we first choose the r who will enter the competition. This can be done in \binom{n}{r} ways. For each of these ways, we can choose k of the r competitors to become finalists in \binom{r}{k} ways. Thus, there are a total of \binom{n}{r} \binom{r}{k} ways to choose the dogs.
Counting Method 2
From the n dogs, choose k who will be the finalists. This can be done in \binom{n}{k} ways. For each of these ways, we can look at the remaining n−k dogs and choose r − k to be the competitors who will not be finalists, in \binom{n-k}{r-k} ways. Thus, there are a total of \binom{n}{r} \binom{n-k}{r-k} ways to choose the dogs. Since both of these solutions count the answer to the same problem, the answers must be equal, so we have \binom{n}{r}\binom{n}{r} = \binom{n}{r} \binom{n-k}{r-k}.
3) COMBINATORIAL PROOF. We will count the number of ways to choose a random sample of n people from a class of n men and n women.
Counting Method 1
From the 2n total people, choose n of them for the random sample. This can be done in \binom{2n}{n} ways.
Counting Method 2
Let r represent the number of men who will be in the sample. Notice that r may have any value from 0 up to n. We divide the problem into these n + 1 cases, and take the sum of all of the answers. In each case, we can choose the r men for the sample from the n men, in \binom{n}{r} ways. For each of these ways, from the n women, we choose r who will not be part of the sample (so the remaining n − r will be in the sample, for a total of r + n − r = n people in the sample). There are \binom{n}{r} ways to do this. Thus the total number of ways of choosing r men and n − r women for the sample is \binom{n}{r}^2. Adding up the solutions for all of the cases, we obtain a final answer of \sum_{r=0}^{n} = \binom{n}{r}^2.
Since both of these solutions count the answer to the same problem, the answers must be equal, so we have \sum_{r=0}^{n} = \binom{n}{r}^2 = \binom{2n}{n}.
Solutions to Exercise 4.2.3
1) We could use this expression to count the number of ways of choosing one leader and some number (which could be zero) of other team members for a project, from a group of n people. There are n ways to choose the leader, and for each of these, there are 2^{n−1} ways of choosing a subset of the other n − 1 people to be team members.
3) We could use this expression to count the number of ways of starting with a collection of n books, choosing r books to put out on bookshelves and some other number (which could be zero) of other books to keep but not display. We break this down into cases depending on the total number k of books that are kept (including the displayed books), which could be anywhere from r up to n. We will take the sum of all of the answers. In each case, there are \binom{n}{r} ways of choosing the k books to keep, and for each such choice, there are \binom{k}{r} ways of choosing the r books to display from the books that are kept. Thus, there are a total of \sum_{k=r}^{n} = \binom{n}{r} \binom{k}{r} solutions to this problem.
Solutions for Chapter 5
Solutions to Exercise 5.1.1
2) There are 6^3 ways for the teacher gifts to be chosen (each child can choose any one of the six types of prizes to give to his teacher). There are \left( \binom{6}{3} \right) ways for Kim to choose his other three prizes; \left( \binom{6}{2} \right) ways for Jordan to choose his other two prizes, and \left( \binom{6}{5} \right) ways for Finn to choose his other five prizes. Thus, the total number of ways for the prizes (including teacher gifts) to be chosen is
\begin{equation} \begin{split} 6^3 \left( \binom{6}{3} \right)\left( \binom{6}{2} \right)\left( \binom{6}{5} \right) &= 6^3 \binom{6+3-1}{3} \binom{6+2-1}{2} \binom{6+5-1}{5} \\[0.25in] &= 6^3 \binom{8}{3} \binom{7}{2} \binom{10}{5} \\[0.25in] &= 6^3· 56 · 21 · 252 = 64,012,032 \end{split} \end{equation}
3) Since the judges must choose at least one project from each age group, this is equivalent to a problem in which they are choosing only six projects to advance, with no restrictions on how they choose them. They can choose six projects from three categories in \left( \binom{3}{6} \right) = \binom{3 + 6 − 1}{6} = \binom{8}{6} = 28 ways.
Solutions to Exercise 5.1.2
1) COMBINATORIAL PROOF. We will count the number of ways of choosing k items from a menu that has n different entries (including mac and cheese), in two ways.
Counting Method 1
By definition, the answer to this is \left( \binom{n}{k} \right).
Counting Method 2
We divide our count into two cases, according to whether or not we choose any orders of mac and cheese. If we do not choose any mac and cheese, then we must choose our k items from the other n − 1 entries on the menu. We can do this in \left( \binom{n-1}{k} \right) ways. If we do choose at least one order of mac and cheese, then we must choose the other k − 1 items from amongst the n entries on the menu (with mac and cheese still being an option for additional choices). We can do this in \left( \binom{n}{k-1} \right) ways. By the sum rule, the total number of ways of making our selection is \left( \binom{n-1}{k} \right) + \left( \binom{n}{k-1} \right).
Since both of these methods are counting the same thing, the answers must be equal, so \left( \binom{n}{k} \right) = \left( \binom{n-1}{k} \right) + \left( \binom{n}{k-1} \right).
Solutions to Exercise 5.2.1
1) There are 14 words in the list. The word “the” appears three times; the words “on” and “child” appear twice each; the other seven words each appear once. Thus, the number of “poems” (orderings of the set) is
\binom{14}{3, 2, 2, 1, 1, 1, 1, 1, 1, 1} = \dfrac{14!}{3!2!2!} = 3,632,428,800.
Solutions for Chapter 6
Solutions to Exercise 6.1.1
1) Various formulas are possible. Most simply, the sequence can be described by the recurrence relation s_1 = 4, s_i = 2s_{i−1} + 1 for i ≥ 2. With this description, the next term is s_5 = 2(39) + 1 = 79.
3) Adjusting the recurrence relation from Example 6.1.3, we obtain the new relation
r_n = r_{n−1} − 20 + .01(r_{n−1} − 20).
This simplifies to r_n = 1.01(r_{n−1} − 20). We still have r_0 = 2000. We now have
r_1 = 1.01(r_0 − 20) = 1.01(1980) = 1999.80.
Stavroula is (marginally) losing money from the beginning. This situation will only get worse as her starting balance each year dwindles.
Solutions to Exercise 6.2.1
1) PROOF. Base case: n = 1. We have b_1 = 5 and 5 + 4(1 − 1) = 5, so b_n = 5 + 4(n − 1) when n = 1.
Inductive step: We begin with the inductive hypothesis. Let k ≥ 1 be arbitrary, and suppose that the equality holds for n = k; that is, assume that b_k = 5 + 4(k − 1). Now we want to deduce that
b_{k+1} = 5 + 4(k + 1 − 1) = 5 + 4k.
Using the recursive relation, we have b_{k+1} = b_k + 4 since k + 1 ≥ 2. Using the inductive hypothesis, we have b_k = 5 + 4(k − 1). Putting these together gives
b_{k+1} = 5 + 4(k − 1) + 4 = 5 + 4k − 4 + 4 = 5 + 4k = 5 + 4(k + 1 − 1),
as desired. This completes the proof of the inductive step.
By the Principle of Mathematical Induction, b_n = 5 + 4(n − 1) for every n ≥ 1.
3) PROOF. Base case: n = 0. We have 0! = 1 (by definition) and n = 0, so n! = 1 ≥ 0 = n. Thus, n! ≥ n when n = 0.
Inductive step: We begin with the inductive hypothesis. Let k ≥ 0 be arbitrary, and suppose that the inequality holds for n = k; that is, assume that k! ≥ k. Now we want to deduce that (k + 1)! ≥ k + 1. Using the definition of factorial, we have (k + 1)! = (k + 1)k! since k + 1 ≥ 0 + 1 = 1. Using the inductive hypothesis, we have k! ≥ k. Putting these together gives
(k + 1)! = (k + 1)k! ≥ (k + 1)k.
If k ≥ 1, then
(k + 1)k ≥ (k + 1)1 = k + 1
and we are done. If k = 0, then (k + 1)! = 1! = 1 = k + 1.
By the Principle of Mathematical Induction, n! ≥ n for every n ≥ 0.
Solutions to Exercise 6.3.1
2) PROOF. Base cases: We will have four base cases: n = 12, n = 13, n = 14, and n = 15.
For n = 12, I can get $12 onto my gift card by buying three increments of $4, since 4 + 4 + 4 = 12.
For n = 13, I can get $13 onto my gift card by buying two increments of $4 and one of $5, since 4 + 4 + 5 = 13.
For n = 14, I can get $14 onto my gift card by buying two increments of $5 and one of $4, since 4 + 5 + 5 = 14.
For n = 15, I can get $15 onto my gift card by buying three increments of $5, since 5 + 5 + 5 = 15.
Inductive step: We begin with the (strong) inductive hypothesis. Let k ≥ 15 be arbitrary, and assume that for every integer i with k − 3 ≤ i ≤ k, I can put $i onto my gift card.
Now I want to deduce that I can put $(k+1) onto my gift card. Using the inductive hypothesis in the case i = k − 3, I see that add can put $(k − 3) onto my gift card by buying increments of $4 or $5. Now if I buy one additional increment of $4, I have put a total of $(k − 3 + 4) = $(k + 1) onto my gift card, as desired. This completes the proof of the inductive step.
By the (strong) Principle of Mathematical Induction, I can put any amount of dollars that is at least $12 onto my gift card.
Solutions for Chapter 7
Solutions to Exercise 7.1.1
2) Since the nth term of the sequence is 2n, the generating function is \sum_{n=0}^{\infty} 2^nx^n.
3) The generating function is 1 + 5x + 10x^2 + 15x^3 + 10x^ + 5x^5 + x^6.
Solutions to Exercise 7.2.1
1) We have \binom{−5}{7} = (−1)^7 \binom{5 + 7 − 1}{7} = − \binom{11}{7} = −330.
2) By the Generalised Binomial Theorem, the coefficient of y^4 in (1 + y)^{−2} is \binom{−2}{4}, so (replacing y with −x) the coefficient of x^4 in (1 − x)^{−2}/ is
(−1)^4 · \binom{−2}{4} = (1) · \dfrac{(−2)(−3)(−4)(−5)}{4!} = 5.
Solutions to Exercise 7.3.1
1) PROOF. Base case: n = 1. The left-hand side of the equation in this case is 1+x. The right-hand side is \dfrac{1 − x^2}{1 − x}. Since 1 − x^2 = (1 − x)(1 + x), we can rewrite the right-hand side as \dfrac{(1 − x)(1 + x)}{1 − x}. Cancelling the 1 − x from the top and bottom gives 1 + x, so the two sides are equal. Since a generating function is a formal object, x is acting as a placeholder, and we do not need to worry about the possibility that 1 − x = 0 that would prevent us from cancelling these factors. Inductive step: Let k ≥ 1 be arbitrary, and suppose that
1 + · · · + x^k = \dfrac{1 − x^{k+1}}{1 − x}.
Now we must deduce that
1 + · · · + x^{k+1} = \dfrac{1 − x^{k+2}}{1 − x}.
We have
1 + · · · + x^{k+1} = (1 + · · · + x^{k})+ x^{k+1}
Applying our inductive hypothesis, this is \dfrac{1 − x^{k+1}}{1 − x} + x^{k+1}. Adding this up over a common denominator of 1 − x gives
\dfrac{1 − x^{k+1} + x^{k+1} − x^{k+2}}{1-x} = \dfrac{1-x^{k+2}}{1-x}
as desired.
By the Principle of Mathematical Induction,
1 + · · · + x^n = \dfrac{1-x^{n+1}}{1-x}
for every n ≥ 1.
4) The generating function for this problem is
(x + x^2 + x^3 + x^4 + x^5 + x^6 )^5 .
We can rewrite this as
x^5 (1 + x + x^2 + x^3 + x^4 + x^5 )^5 .
Finding the coefficient of x^{11} in this expression is equivalent to finding the coefficient of x^6 in
(1 + x + x^2 + x^3 + x^4 + x^5 )^5 = \left( \dfrac{1 − x^6}{1 − x} \right)^5.
Using the Binomial Theorem and substituting y = −x^6, we see that
\begin{equation} \begin{split} (1 − x^6)^5 &= (−x^6)^0 + \binom{5}{1} (−x^6)^1 + \binom{5}{2} (−x^6)^2 + \binom{5}{3} (−x^6)^3 + \binom{5}{4} (−x^6)^4 + (−x^6)^5 \\ &= 1 − 5x^6 + 10x^{12} − 10x^{18} + 5x^{24} − x^{30}. \end{split} \end{equation}
The function we’re interested in is the product of this with (1−x)^{−5}, and we are looking for the coefficient of x^6. The only ways of getting an x^6 term from this product are by taking the x^0 term above and multiplying it by the x^6 term from (1 − x)^{−5}, or by taking the x^6 term above and multiplying it by the x^0 term from (1 − x)^{−5}.
Using the Generalised Binomial Theorem (and substituting y = −x), the coefficient of x^0 in (1 − x)^{−5} is
(-1)^0 \binom{-5}{0} = (-1)^0 (-1)^0 \binom{5+0-1}{0} = 1
Similarly, the coefficient of x^6 in (1 − x)^{−5} is
(-1)^6 \binom{-5}{6} = (-1)^6 (-1)^6 \binom{5+6-1}{6} = \binom{10}{6} = 210
Thus, the number of ways in which Trent can roll a total of 11 on his five dice is the coefficient of x^{11} in our generating function, which is \binom{10}{6} − 5 = 205. The probability of this happening is 205 divided by the total number of outcomes of his roll, which is 6^5 = 7776, so \dfrac{205}{7776}, or about 2.5\%.
Solutions for Chapter 8
Solutions to Exercise 8.1.1
1) First we rewrite the generating function as a sum of two parts:
\dfrac{1}{(1 + 2x)(2 − x)} = \dfrac{A}{1 + 2x} + \dfrac{B}{2-x} = \dfrac{A(2 − x) + B(1 + 2x)}{(1 + 2x)(2 − x)}.
Now the numerator gives 2A + B + (2B − A)x = 1 as polynomials. Hence we must have 2B − A = 0 and 2A + B = 1. Combining these gives B = \dfrac{1}{5} and A = \dfrac{2}{5}. Thus the given generating function is equal to
\dfrac{2}{5} (1+2x)^{-1} + \dfrac{1}{5} (2-x)^{-1} = \dfrac{2}{5} (1+2x)^{-1} + \dfrac{1}{10} (1- \dfrac{1}{2}x)^{-1}
Using the Generalised Binomial Theorem, the coefficient of x^r in the first of these summands is \dfrac{2}{5}(−1)^r 2^r, while the coefficient of x^r in the second summand is \dfrac{1}{10} \left( \dfrac{1}{2} \right)^r. Thus, the coefficient of x^r is \dfrac{2}{5}(−1)^r 2^r + \dfrac{1}{10} \left( \dfrac{1}{2} \right)^r.
3) First we rewrite the generating function as a sum of three parts:
\begin{equation} \begin{split} \dfrac{1 + 2x}{(1 − 2x)(2 + x)(1 + x)} &= \dfrac{A}{1 − 2x} + \dfrac{B}{2+x} + \dfrac{C}{1+x} \\[0.25in] &= \dfrac{A(2 + x)(1 + x) + B(1 − 2x)(1 + x) + C(1 − 2x)(2 + x)}{(1 − 2x)(2 + x)(1 + x)} \end{split} \end{equation}
Now the numerator gives
\begin{equation} \begin{split} & A(2 + 3x + x^2) + B(1 − x − 2x^2) + C(2 − 3x − 2x^2) \\[0.25in] =\;\;& 2A + B + 2C + (3A − B − 3C)x + (A − 2B − 2C)x^2 = 1 + 2x \end{split} \end{equation}
as polynomials, so we have 2A + B + 2C = 1, 3A − B − 3C = 2, and A − 2B − 2C = 0. Solving this gives C = \dfrac{−1}{3}, B = \dfrac{3}{5}, and A = \dfrac{8}{15}. Thus (taking a factor of 2 out of the denominator of the second piece) the given generating function is equal to
\dfrac{8}{15} (1 − 2x)^{−1} + \dfrac{3}{10} (1 + \dfrac{1}{2}x)^{−1} - \dfrac{1}{3} (1 + x)^{−1}.
Using the Generalised Binomial Theorem, the coefficient of x^r in the first of these summands is \dfrac{8}{15} 2^r; the coefficient of x^r in the second summand is \dfrac{3}{10} (−1)^r \left( \dfrac{1}{2} \right)^r; and the coefficient of x^r in the third summand is −\dfrac{1}{3} (−1)^r. We conclude that the coefficient of x^r in this generating function is
\dfrac{8}{15} 2^r = \dfrac{3}{10}(-1)^{r} \left( \dfrac{1}{2} \right)^r - \dfrac{1}{3}(-1)^r
Solutions to Exercise 8.2.1.
2) To use the method of partial fractions, we first factor the denominator:
2x^2 + x − 1 = (2x − 1)(x + 1).
Now, write
\begin{equation} \begin{split} f(x) &= \dfrac{2+x}{2x^2 + x − 1} = \dfrac{2+x}{(2x − 1)(x + 1)} = \dfrac{A}{2x-1} + \dfrac{B}{x+1} \\[0.25in] &= \dfrac{A(x + 1) + B(2x − 1)}{(2x − 1)(x + 1) } = \dfrac{(A − B) + (A + 2B)x}{2x^2 + x − 1} \end{split} \end{equation}
Equating the coefficients in the numerators yields the 2 equations
A − B = 2, \;\;\;\; A + 2B = 1.
Subtracting the second equation from the first tells us that −3B = 1, so B = −\dfrac{1}{3}. Then the first equation tells us that A = 2 − \left( \dfrac{1}{3} \right) = \dfrac{5}{3}. So we have
f(x) = \dfrac{\dfrac{5}{3}}{2x-1} - \dfrac{\dfrac{1}{3}}{x+1} = \dfrac{\dfrac{5}{3}}{1-2x} - \dfrac{\dfrac{1}{3}}{1+x}
The coefficient of x^r in \dfrac{1}{(1 − x)} is 1, so
- the coefficient of x^r in \dfrac{1}{(1 − 2x)} is 2^r (by replacing x with 2x), and
- the coefficient of x^r in \dfrac{1}{(1 + x)} is (−1)^r (by replacing x with −x)
Therefore, the coefficient of x^r in the generating function f(x) is
-\dfrac{5}{3}(2^r) -\dfrac{1}{3}(-1)^r
Solutions to Exercise 8.3.1
Let C(x) = \sum_{n=0}^{\infty} c_nx^n be the generating function of \{c_n\}. Then
\begin{equation} \begin{split} C(x) &= c_0 &+ c_1x &+ c_2x^2 &+ c_3x^3 &+ c_4x^4 &+ ... \\ xC(x) &= &+ c_0x &+ c_1x^2 &+ c_2x^3 &+ c_3x^4 &+ ... \\ x^2C(x) &= & &+ c_0x^2 &+ c_1x^3 &+ c_2x^4 &+ ... \\ \end{split} \end{equation}
so
\begin{equation} \begin{split} (1 − x − 2x^2)C(x) &= C(x) − xC(x) − 2x^2C(x)\\ &= c_0 + (c_1 − c_0)x + \sum_{n=2}^{\infty} (c_n − c_{n−1} − 2c_{n−2})x^n\\ &= c_0 + (c_1 − c_0)x \end{split} \end{equation}
since (by the recurrence relation) we have c_n − c_{n−1} − 2c_{n−2} = 0 for n ≥ 2. Therefore
C(x) = \dfrac{c_0 + (c_1 − c_0)x}{1 − x − 2x^2}
Since c_0 = 2 and c_1 = 0, this means
C(x) = \dfrac{2 + (0 − 2)x}{1 − x − 2x^2} = \dfrac{2-2x}{(1 + x)(1 − 2x)}.
We now use partial fractions. Write
\dfrac{2-2x}{(1 + x)(1 − 2x)} = \dfrac{A}{1+x} + \dfrac{B}{1 − 2x} = \dfrac{A(1 − 2x) + B(1 + x)}{(1 + x)(1 − 2x)} = \dfrac{(A + B) + (B − 2A)x}{(1 + x)(1 − 2x)}.
Equating the coefficients in the numerators yields the equations
2 = A + B,\;\;\;\; −2 = B − 2A.
Subtracting the second equation from the first tells us that
2 − (−2) = (A + B) − (B − 2A) = 3A
so A = \dfrac{4}{3}. Then the second equation tells us that
B = 2A − 2 = 2\left( \dfrac{4}{3} \right) − 2 = \dfrac{2}{3}.
So
C(x) = \dfrac{2-2x}{(1 + x)(1 − 2x)} = \dfrac{A}{1+x} + \dfrac{B}{1 − 2x} = \dfrac{\dfrac{4}{3}}{1+x} = \dfrac{\dfrac{2}{3}}{1-2x} = \dfrac{4}{3} \left( \dfrac{1}{1+x} \right) + \dfrac{2}{3} \left( \dfrac{1}{1-2x} \right)
From the generalized binomial theorem, we know:
- The coefficient of x^n in \dfrac{1}{1 + x} = (1 + x)^{−1} is
\binom{-1}{n} = (-1)^n \binom{1 + n -1}{n} = (-1)^n \binom{n}{n} = (-1)^n
- The coefficient of x^n in \dfrac{1}{1 − 2x} = (1 − 2x)^{−1} is
\binom{-1}{n} (-2)^n = (-1)^n \binom{1 + n -1}{n} (-2)^n = (-1)^{2n} \binom{n}{n} 2^n = 2^n
Therefore c_n, the coefficient of x^n in C(x), is \dfrac{4}{3} (−1)^n + \dfrac{2}{3} · 2^n.
3) Let E(x) = \sum_{n=0}^{\infty} e_nx^n be the generating function of \{e_n\}. Then
\begin{equation} \begin{split} E(x) &= e_0 &+ e_1x &+ e_2x^2 &+ e_3x^3 &+ e_4x^4 &+ ... \\ xE(x) &= &+ e_0x &+ e_1x^2 &+ e_2x^3 &+ e_3x^4 &+ ... \\ \dfrac{1}{1-x} &= 1&+ x&+ x^2 &+ x^3 &+ x^4 &+ ... \\ \end{split} \end{equation}
so
\begin{equation} \begin{split} (1 − 3x)E(x) + \dfrac{2}{1-x} &= E(x) − 3xE(x) + 2 · \dfrac{1}{1-x}\\ &= (e_0 + 2) + \sum_{n=2}^{\infty} (e_n − 3e_{n−1} + 2)x^n\\ &= (e_0 + 2), \end{split} \end{equation}
since (by the recurrence relation) we have e_n − 3e_{n−1} + 2 = 0 for n ≥ 1. Therefore
E(x) = \dfrac{(e_0 + 2) − \dfrac{2}{1-x}}{1 − 3x} = \dfrac{(e_0 + 2)(1 − x) − 2}{(1 − 3x)(1 − x)}
Since e_0 = 2, this means
E(x) = \dfrac{(2 + 2)(1 − x) − 2}{(1 − 3x)(1 − x)} = \dfrac{2-4x}{(1 − 3x)(1 − x)} .
We now use partial fractions. Write
\dfrac{2-4x}{(1 - 3x)(1 − x)} = \dfrac{A}{1-3x} + \dfrac{B}{1 − x} = \dfrac{A(1 − x) + B(1 − 3x)}{(1 − 3x)(1 − x)} = \dfrac{(A + B) − (A + 3B)x}{(1 − 3x)(1 − x)}
Equating the coefficients in the numerators yields the equations
2 = A + B,\;\;\;\; −4 = −(A + 3B)
Adding the two equations tells us that 2 − 4 = (A + B) − (A + 3B) = −2B, so B = 1. Then the first equation tells us that A = 2 − B = 2 − 1 = 1. So
E(x) = \dfrac{2-4x}{(1 - 3x)(1 − x)} = \dfrac{A}{1-3x} + \dfrac{B}{1 − x} = \dfrac{1}{1-3x} + \dfrac{1}{1-x}
From the generalized binomial theorem, we know that the coefficient of x^n in \dfrac{1}{1 − 3x} is 3n, and the coefficient of x^n in \dfrac{1}{1 − x} is 1. Therefore e_n, the coefficient of x^n in E(x), is 3^n + 1.
Solutions for Chapter 9
Solutions to Exercise 9.1.1
2) To prove Proposition 9.1.1 requires strong induction, since the recursive relation calls on two previous terms. Thus, two base cases are required.
3) The formula from Proposition 9.1.1 gives
\begin{equation} \begin{split} D_5 &= 5! \left( \dfrac{(-1)^0}{0!} +\dfrac{(-1)^1}{1!} + \dfrac{(-1)^2}{2!} + \dfrac{(-1)^3}{3!} + \dfrac{(-1)^4}{4!} + \dfrac{(-1)^5}{5!} \right) \\ &= 120 \left( 1 − 1 + \dfrac{1}{2} − \dfrac{1}{6} + \dfrac{1}{24} − \dfrac{1}{120} \right) \\ &= 60 − 20 + 5 − 1 = 44. \end{split} \end{equation}
4) The initial conditions are D_1 = 0 and D_2 = 1. The recursive relation D_n = (n − 1)(D_{n−1} + D_{n−2}) for n ≥ 3 gives D_3 = 2(D_2 + D_1) = 2(1 + 0) = 2.
Now
D_4 = 3(D_3 + D_2) = 3(2 + 1) = 9,
and
D_5 = 4(D_4 + D_3) = 4(9 + 2) = 4(11) = 44.
Solutions to Exercise 9.2.1
1) PROOF. Base case: n = 0. We have c_0 = 1 (by definition) and 1 > 0, so c_0 > 0.
Inductive step: We begin with the inductive hypothesis. We will require strong induction. Let k ≥ 0 be arbitrary, and suppose that the inequality holds for every j with 0 ≤ j ≤ k; that is, assume that for every such j, c_j > 0.
Now we want to deduce that c_{k+1} > 0. Using the recursive relation, we have
c_{k+1} = \sum_{i=0}^{k} c_ic_{(k+1)−i−1} = \sum_{i=0}^{k} c_ic_{k-i}
Using the inductive hypothesis, we have c_j > 0 for every j such that 0 ≤ j ≤ k. Putting these together gives that c_{k+1} is a sum of k + 1 terms where each term has the form c_ic_{k−i} with 0 ≤ i ≤ k. Since 0 ≤ k − i ≤ k, we see that c_i > 0 and c_{k−i} > 0 so that c_ic_{k−i} > 0. Hence
c_{k+1} = \sum_{i=0}^{k} c_ic_{k-i} > 0
This completes the proof of the inductive step.
By the Principle of Mathematical Induction, c_n > 0 for every n ≥ 0.
Solutions to Exercise 9.3.1
1)
\begin{equation} \begin{split} B_4 = \sum_{k=1}^{4} \binom{3}{k-1} B_{4−k} &= \binom{3}{0}B_3 + \binom{3}{1}B_2 + \binom{3}{2}B_1 + \binom{3}{3}B_0 \\ &= 5 + 3(2) + 3(1) + 1(1) = 15. \end{split} \end{equation}
3) If b_i = \dfrac{(i + 1)!}{2} then the expanded exponential generating function for this sequence is
\sum_{i=0}^{\infty} \dfrac{b_ix^i}{i!} = \sum_{i=0}^{\infty} \dfrac{(i + 1)!x^i}{2i!} = \sum_{i=0}^{\infty} \dfrac{(i + 1)x^i}{2}.
This is
\dfrac{1}{2} \sum_{i=0}^{\infty} (i + 1)x^i = \dfrac{1}{2} \left( \sum_{i=0}^{\infty} (i+1)x^i \right) = \dfrac{1}{2(1-x)^2}
Solutions for Chapter 10
Solutions to Exercise 10.1.1
1) Since there are 8 rows on a chessboard, and 17 > 2(8), the Generalised Pigeonhole Principle says that there must be at least 2 + 1 = 3 rooks that are all in the same row of the board. Choose such a row, and call it Row A. Note that Row A contains at most 8 rooks.
There are at least 17 − 8 = 9 rooks that are not in Row A. Since there are 7 other rows on the chessboard, and 9 > 1(7), the Pigeonhole Principle says that there must be at least 1 + 1 = 2 rooks that are in the same row, from amongst the other rows of the board. Choose such a row, and call it Row B. Note that Row B also contains at most 8 rooks.
There is at least 17−8−8 = 1 rook remaining, so there must be a rook somewhere on the board that is in neither Row A nor Row B. Choose such a rook, Rook 1, and call the row that it is in Row C. Since there are at least 2 rooks in Row B, at least one of them must not be in the same column as Rook 1. Choose such a rook, Rook 2. Since there are at least 3 rooks in Row A, at least one of them must not be in the same column as either Rook 1 or Rook 2. Choose such a rook, and call it Rook 3. Now Rooks 1, 2, and 3 do not threaten each other, so fulfill the requirements of the problem.
3) We use the even more generalised pigeonhole principle with n − 1 = 15 for the adults, and n_2 = 23 for the children (and m = 2 categories: adults and children). The principle tells us that as long as at least
n_1 + n_2 − m + 1 = 15 + 23 − 2 + 1 = 37
people are approached, he will have enough people to carry his art in the parade.
Solutions to Exercise 10.2.2
2) Of the basic pieces of information that we need to complete a Venn diagram, one has not been given to us: the number of Kevin’s apps that are free and require internet access. Fortunately, we can use inclusion-exclusion to work this out from the others. We use F to represent the set of free apps; G to represent the games, and I to represent the apps that require internet. Then we have been told:
|F| = 78, |I| = 124, |G| = 101, |F ∩ G| = 58, |G ∩ I| = 62, |F ∩ G ∩ I| = 48, |F ∪ G ∪ I| = 165.
Using inclusion-exclusion, we have
165 = 78 + 124 + 101 − 58 − 62 − |F ∩ I| + 48,
so
|F ∩ I| = 78 + 124 + 101 − 58 − 62 + 48 − 165 = 66.
The value we have been asked for is
|F ∩ I ∩ \overline{G}| = |F ∩ I| − |F ∩ I ∩ G| = 66 − 48 = 18.
3) The number of integers between 1 and 60 that are divisible by 2 is \dfrac{60}{2} = 30. Call the set of these integers A. The number of integers between 1 and 60 that are divisible by 3 is \dfrac{60}{3} = 20. Call the set of these integers B. The number of integers between 1 and 60 that is divisible by 5 is \dfrac{60}{5} = 12. Call the set of these integers C. Then |A ∩ B| is the number of integers between 1 and 60 that are divisible by 2 and 3; that is, the number that are divisible by 6. This is \dfrac{60}{6} = 10. Similarly, |A ∩ C| is the number of integers between 1 and 60 that are divisible by 2 and 5; that is, the number that are divisible by 10. This is \dfrac{60}{10} = 6. Also, |B ∩ C| is the number of integers between 1 and 60 that are divisible by 3 and 5; that is, the number that are divisible by 15. This is \dfrac{60}{15} = 4. Finally, |A ∩ B ∩ C| is the number of integers between 1 and 60 that are divisible by 2, 3, and 5; that is, the number that are divisible by 30. This is \dfrac{60}{30} = 2.
We have been asked for |A ∪ B ∪ C|. Using inclusion-exclusion, we see that the answer is 30 + 20 + 12 − 10 − 6 − 4 + 2 = 44.
Solutions for Chapter 11
Solutions to Exercise 11.2.1
1) a) The only edge incident with a is e_1, so the valency of a is 1.
b) The only edge incident with b is e_2, so the valency of b is 1.
c) The edges incident with c are e_1, e_3, and e_4, so the valency of c is 3.
d) The edges incident with d are e_2, e_3, and e_5, so the valency of d is 3.
e) The edges incident with e are e_4, e_5, and e_6, so the valency of e is 3.
Since e_6 = \{e, e\} is a loop, the graph is not simple. There is no isolated vertex, because no vertex has valency 0. The only neighbour of a is c, and the only edge incident with a is e_1.
3) a) The edges incident with a are e_1 and e_2, so the valency of a is 2.
b) The edges incident with b are e_1 and e_3, so the valency of b is 2.
c) The edges incident with c are e_2 and e_3, so the valency of c is 2.
d) No edges are incident with d, so the valency of d is 0.
There are no loops or multiple edges, so the graph is simple. The graph does have an isolated vertex, namely, d (because the valency of d is 0). The neighbours of a are b and c, and the edges incident with a are e_1 and e_2, as was already mentioned above.
Solutions to Exercise 11.3.1.
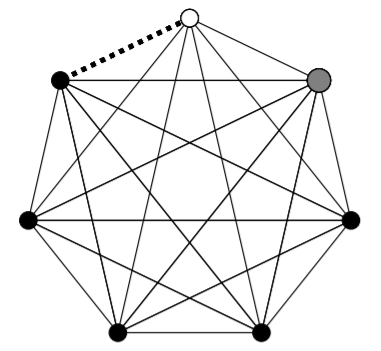
3) In the following picture, the dotted line represents the edge we will delete. If we then delete the white vertex, the graph that remains is complete. If instead we then delete the large grey vertex (which is the next one clockwise from the white vertex), the remaining graph will not be complete, since the white vertex is only adjacent to four of the five black vertices.
4) PROOF. Let G be a graph with e edges.
Base case: e = 0. Since G has no edges, every vertex has valency 0. So the number of vertices of odd valency is 0, which is even.
Inductive step: We begin with the inductive hypothesis. Fix e ≥ 0, and assume that every graph with e edges has an even number of vertices of odd valency.
Now we want to deduce that every graph with e + 1 edges has an even number of vertices of odd valency. Let H be an arbitrary graph with e+ 1 edges. Choose one edge f (there is one since e + 1 ≥ 1), and call its endvertices u and v. Let H' = H \setminus \{f\}.
Notice that H' has e + 1 − 1 = e edges, so our induction hypothesis applies to H'. Therefore, H' has an even number of vertices of odd valency. Call this number 2m, where m ∈ \mathbb{Z}.
Observe that the valency of every vertex of H is the same as its valency in H' if the vertex is not u or v, and is one greater than its valency in H' if the vertex is either u or v. Consider the three possible cases: u and v both have even valency in H'; u and v both have odd valency in H'; or exactly one of u and v has even valency in H'.
If u and v both have even valency in H', then they both have odd valency in H, so the number of vertices of odd valency in H must be 2m + 2, which is even.
If u and v both have odd valency in H', then they both have even valency in H, so the number of vertices of odd valency in H must be 2m − 2, which is even.
If exactly one of u and v has even valency in H', then exactly one of u and v will have even valency in H (the other one, since the valency of each of u and v goes up by 1). So the number of vertices of odd valency in H must be 2m (even though one of the specific vertices of odd valency has changed between u and v), which is even.
In all cases, H has an even number of vertices of odd valency. This completes the proof of the inductive step.
By the Principle of Mathematical Induction, every graph with at least 0 edges has an even number of vertices of odd valency.
Solutions to Exercise 11.4.1
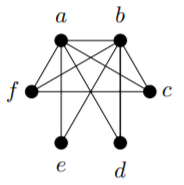
1) The graphs are not isomorphic, because the only vertex of valency 1 in G (namely, c) is adjacent to a vertex of valency 3 (namely d), but the only vertex of valency 1 in H (namely, z) is adjacent only to a vertex of valency 1 (namely, y).
Here is a more complete proof. Suppose \varphi: G → H is an isomorphism. (This will lead to a contradiction.) We must have
d_H \left( \varphi(c) \right) = d_G(c) = 1.
(This principle was pointed out in the proof of Proposition 11.4.1(3).) The only vertex of valency 1 in H is z, so this implies that \varphi(c) = z.
Now, since d ∼ c, we must have \varphi(d) ∼ \varphi(c). Since \varphi(c) = z, and the only neighbour of z is y, this implies \varphi(d) = y. So
d_H(y) = \left( d_H \varphi(d) \right) = d_G(d).
However, d_H(y) = 2 and d_G(d) = 3, so d_H(y) 6= d_G(d). This is a contradiction.
3) There is no vertex of valency 0 in G_1, but A is a vertex of valency 0 in G_2. Therefore G_1 and G_2 do not have the same degree sequence, so they are not isomorphic.
Solutions to Exercise 11.4.2
2) Of the five vertex labels, we can choose any two to join with an edge. Thus, the number of labeled graphs on five vertices with one edge is \binom{5}{2} = 10.
3) Notice that there are \binom{5}{2} = 10 total edges possible in a graph on 5 vertices. Thus, the number of labeled graphs on 5 vertices with 3 edges is the number of ways of choosing 3 of these 10 labeled edges. So there are \binom{10}{3} = 120 labeled graphs on 5 vertices that have 3 edge.
Similarly, there are \binom{10}{4} = 210 labeled graphs on 5 vertices that have 4 edges. Thus, in total there are 120 + 210 = 330 labeled graphs on 5 vertices that have 3 or 4 edges.
Solutions for Chapter 12
Solutions to Exercise 12.1.1
1) PROOF. We prove, by induction on n, that if n ≥ 1, and G is any digraph with n vertices that has no loops or multiarcs, then
|A(G)| = \sum_{v∈V (G)} d_G^+ (v) = \sum_{v∈V (G)} d_G^-(v)
Base case: n = 1. Let G be a digraph with no loops or multiarcs, and with only one vertex v_1. Then there are no arcs in G, so |A(G)| = 0 = d_G^+ (v_1) = d_G^- (v_1). So the desired conclusion is true when n = 1.
We now establish the induction step. Assume that n ≥ 1, the formula holds for every digraph with n vertices that has no loops or multiarcs, and G is a digraph with n + 1 vertices that has no loops or multiarcs.
Pick an arbitrary vertex u of G. Let
- N^+ be the set of outneighbours of u, and N^− the set of inneighbours of u,
- s = |N +| = d + G (u) be the number of arcs that begin at u,
- t = |N −| = d − G (u) be the number of arcs that end at u, and
- G' be the digraph obtained from G by deleting u and its s + t incident arcs.
Note that:
- V (G') = V (G) \setminus {u}, so G' has n vertices.
- |A(G')| = |A(G)| − s − t.
- For v ∈ V (G') \setminus N^−, we have d_{G'}^+(v) = d_G^+ (v) (because the outneighbours of v in G' are exactly the same as the outneighbours of v in G).
- For v ∈ N^−, we have d_G^+ (v) = d_G^+ (v)−1 (because u is counted as an outneighbour of v in G, but it is not in G' so it cannot be counted as an outneighbour in G').
- Similar statements hold with N^− replaced by N^+.
Hence
\begin{equation} \begin{split} \sum_{v∈V (G)} d_G^+(v) &= \sum_{v∈V (G) \setminus (N^−∪\{u\})} d_G^+(v) + \sum_{v∈N^−} d_G^+(v) + \sum_{v∈\{u\}} d_G^+(v) \\[0.125in] &= \sum_{v∈V (G) \setminus (N^−∪\{u\})} d_{G'}^+(v) + \sum_{v∈N^−} \left( d_{G'}^+(v) +1 \right) + d_{G'}^+(u) \\[0.125in] &= \left( \sum_{v∈V (G) \setminus (N^−∪\{u\})} d_{G'}^+(v) + \sum_{v∈N^−} d_{G'}^+(v) \right) + |N^−| + d_{G'}^+(u)\\[0.125in] &= \sum_{v∈V (G')} d_{G'}^+(v) + t + s\\[0.125in] &= |A(G')| + s + t \;\;\;\;\;(\text{induction hypothesis}) \\[0.125in] &= |A(G)|. \end{split} \end{equation}
Similarly, we can argue that \sum_{v∈V (G)} d^−G(v) = |A(G)|. This completes the inductive step and the proof.
3) Beginning at the top and working clockwise, label the vertices of the digraph a, b, c, d, and e. Then:
- a has outvalency 2 and invalency 1;
- b has outvalency 2 and invalency 2;
- c has outvalency 1 and invalency 2;
- d has outvalency 2 and invalency 2;
- e has outvalency 1 and invalency 1.
Solutions to Exercise 12.2.1
2) This graph is connected. To see this, note that (a, j, g, v, e, d, i, h, c, b) is a walk that passes through all of the vertices of G, so it is possible to walk from a to any other vertex. Therefore, the connected component that contains a is V(G) = \{a, b, c, d, e, f, g, h, i, j\}. There are several walks of length 5 from a to f. One example is (a, g, a, j, g, f).
3) This graph is not connected. To see this, note that there are no edges from any vertex in \{a, d, e, f, g, j\} to any vertex in \{b, c, h, i\}. Indeed the connected component that contains a is \{a, d, e, f, g, j\}. (The walk (a, d, e, f, g, j) passes through all of these vertices, but none of these vertices are adjacent to any vertex that is not in the subset.) There are several walks of length 3 from a to d. One example is (a, d, a, d).
Solutions to Exercise 12.3.1
1) (a) There are many paths of length 3. One example is (a, b, c, h).
(b) (b, c, f, b) is a cycle of length 3.
(c) (a, b, c, b) is neither a path nor a cycle. It is not a path because the vertices are not all distinct. (Namely, the vertex b occurs twice.) It is not a cycle, because the first vertex (namely, a) is not the same as the final vertex (namely, b).
3) PROOF. Let (u = u_1, u_2, . . . , v = u_k, u) be a cycle of G in which u and v appear as consecutive vertices. Let G' = G \setminus \{uv\}.
Let x and y be arbitrary vertices of G. Since G is connected, there is a walk (x = x_1, x_2, . . . , x_m = y) from x to y in G. If this walk does not contain the edge uv then it is also a walk in G'. If it does contain the edge uv, then we can find some i with 1 ≤ i ≤ m − 1 such that either x_i = u and x_{i+1} = v, or vice versa. For every such i, replace the pair (x_i , x_{i+1}) in the walk by either (u = u_1, u_2, . . . , v = u_k) or (v = u_k, u_{k−1}, . . . , u = u_1) (as appropriate, depending on whether x_i = u or x_i = v). The result is a walk from x to y that does not use the edge uv, so is in G'. Since x and y were arbitrary vertices of G', for any two vertices x and y of G' there is an x − y walk, so by definition, G is connected.
Solutions to Exercise 12.4.1
1) PROOF. Let T be a tree, and let v be a leaf of T. Consider T \setminus \{v\}. Certainly it cannot have any cycles, since T has no cycles. Let x and y be arbitrary vertices of T \setminus \{v\}. Since T is connected, there is an x − y walk in T, so by Proposition 12.3.1, there is an x − y path in T. Since v is a leaf of T, if an x − y walk uses the vertex v then the neighbour of v would have to come both before and after v in the walk, since v has only one neighbour, so such a walk would not be a path. Thus, the x − y path cannot use the vertex v, so it is still a path in T \setminus \{v\}. Since x and y were arbitrary vertices, this shows that T \setminus \{v\} is connected. This completes the proof.
3) The two nonisomorphic unlabeled trees on 4 vertices are:

Solutions for Chapter 13
Solutions to Exercise 13.1.1
1) This graph has Euler tours, because it is connected and all vertices have even valency. One Euler tour is (d, f, g, j, a, d, e, i, h, b, f, c, b, i, d). The following figure numbers the vertices 1, 2, 3, . . . in the order they are visited.

Solutions to Exercise 13.2.1
2) (a) In the closure, we can join a to b; we can join a to c; and we can join b to f. This completes the closure, shown below. It is not easy to see from this whether or not the graph has a Hamilton cycle. In fact, it does not.
(b) The closure of this graph is K_6. We can easily see from this that the graph does have a Hamilton cycle. (To see that the closure is K_6, observe that every vertex of the graph has valency at least 2. Thus, the two vertices of valency 4 can be joined to each of their nonneighbours. After doing so, every vertex has valency at least 3, so every vertex can be joined to every other vertex.)
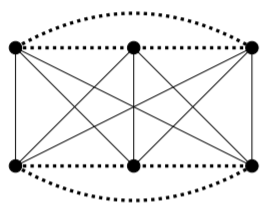
3) Let G be the graph that has been shown here. Using the notation of Theorem 13.2.1, let S = \{a, f\}. Then |S| = 2, but G \setminus S has 3 connected components: \{b, e\}, \{c, h\}, and \{d, g\}. Since 3 > 2, G cannot have a Hamilton cycle.
Solutions for Chapter 14
Solutions to Exercise 14.1.1
1) PROOF. Trees are bipartite (they have no cycles at all, so certainly do not have any cycles of odd length), so Theorem 14.1.3 tells us that they are class one.
2) PROOF. The proof is by contradiction: suppose n is odd, and the cycle
C_n = (v_0, v_1, . . . , v_n = v_0)
is class one. Since every vertex of C_n has valency two, this means that the graph has a proper edge-colouring that uses only 2 colours. Let us call the colours red and blue.
Assume, without loss of generality, that the edge v_0v_1 is red. The edge v_1v_2 cannot be the same colour as v_0v_1 (because they are both incident to v_1), so v_1v_2 must be blue. The edge v_2v_3 cannot be the same colour as v_1v_2 (because they are both incident to v_2), so v_2v_3 must be red. Continuing in this way, we see (by induction on k) that v_kv_{k+1} is red whenever k is even, and it is blue whenever k is odd. (That is, the two colours must alternate red, blue, red, blue, red, blue,. . . as we go around the cycle.)
In particular, since n is odd, we know that n − 1 is even, so this means that the edge v_{n−1}v_n is red. However, we have v_n = v_0 so the edges v_{n−1}v_n and v_0v_1 are both incident to the vertex v_0), so they cannot be the same colour. The contradicts the fact that both edges are red.
Solutions to Exercise 14.2.1
1) The following 2-colouring of the edges of K_6 has no solid triangle and no dotted K_4 (because the solid edges form K_{3,3}, which has no cycles of odd length, and each connected component of the dotted graph is only K_3):
3) PROOF. We prove this by induction on k + \ell. The base case is when k + \ell = 2 (so k = \ell = 1). Then
R(k, \ell) = R(1, 1) = 1 < 4 = 2^{1+1} = 2^{k+ \ell} .
So the inequality is valid in the base case.
For the induction step, assume k + \ell ≥ 2, and that R(k' , \ell ' ) ≤ 2 k' + \ell ', whenever k' + \ell ' < k + \ell. Since R(k, \ell) = R(\ell, k), we may assume k ≤ \ell (by interchanging k and \ell, if necessary). If k = 1, then
R(k, \ell) = R(1, \ell) = 1 = 2^0 < 2^{k + \ell} .
Therefore, we may assume 2 ≤ k ≤ \ell. Since (k − 1) + \ell < k + \ell and k + (\ell − 1) < k + \ell, the induction hypothesis tells us that
R(k − 1, \ell) ≤ 2^{(k−1) + \ell} \text{ and } R(k, \ell − 1) ≤ 2^{k+(\ell−1)} .
Therefore
\begin{equation} \begin{split} R(k, \ell) &≤ R(k − 1, \ell) + R(k, \ell − 1) \\ &≤ 2^{(k−1)+\ell} + 2^{k+(\ell−1)} \\ &= 2^{k+\ell−1} + 2^{k+\ell−1} \\ &= 2 · 2^{k+\ell−1} \\ &= 2^{k+\ell}. \end{split} \end{equation}
This completes the proof.
4) Since R(k, \ell) ≤ R(k' , \ell ') whenever k ≤ k' and \ell ≤ \ell ', we have
40 ≤ R(3, 10) ≤ R(3, 11).
Also, since R(k, \ell) ≤ R(k − 1, \ell) + R(k, \ell − 1) and R(2, \ell) = \ell, we have
R(3, 11) ≤ R(3 − 1, 11) + R(3, 11 − 1) = R(2, 11) + R(3, 10) ≤ 11 + 42 = 53.
So 40 ≤ R(3, 11) ≤ 53.
Solutions to Exercise 14.2.2
2) PROOF. We assume that N − 1 > (c + 1)(n − 1). Consider an arbitrary colouring of the edges of K_N with c + 1 colours. Fix a vertex v. Since v has N − 1 > (n − 1)(c + 1) incident edges, the generalised pigeonhole principle tells us that there must be some set of at least n edges incident with v that are all coloured with the same colour, say colour i. Look at the induced subgraph of K_N on the n other endpoints of these edges. If any edge xy of this induced subgraph is coloured with colour i, then all of the edges of the triangle \{v, x, y\} have been coloured with colour i, so K_N has a monochromatic triangle.
If on the other hand no edge of the induced subgraph has been coloured with colour i, then the induced subgraph is a K_n whose edges have been coloured with the remaining c colours. By hypothesis, every such colouring has a monochromatic triangle. This completes the proof.
Solutions to Exercise 14.2.3
1) We are looking for the smallest value of n such that every edge-colouring of K_n with dotted, dashed, and solid lines has either a dashed K_2 or a dotted K_2 or a solid triangle. The following colouring shows that R(2, 2, 3) > 2:

However, R(2, 2, 3) = 3. This is because if any edges are dotted or dashed, then there is a dotted or dashed K_2; if no edges are dotted or dashed, then every edge is solid, so there is a solid K_3.
2) We will show that R(2, 4) = 4. We are looking for the smallest value of n such that every edge-colouring of K_n with dashed or solid lines has either a dashed K_2 or a solid K_4. The following colouring shows that R(2, 4) > 3;
However, in K_4 if any edge is dashed, then there is a dashed K_2, while if no edges are dashed, then there is a solid K_4.
Solutions to Exercise 14.3.1
2) PROOF. We will proceed by induction on n.
Base case: n = 1. Then K_1 is the graph with one vertex and no edges, and χ(K_1) = 1. Thus, when n = 1 we have χ(K_n) = n.
Induction step: We begin with the induction hypothesis. Let k ≥ 1 be arbitrary, and assume that χ(K_k) = k, so we can properly colour K_k using k colours, and k colours are required to do so.
Now consider the graph K_{k+1}. Let v be an arbitrary vertex of this graph. By our induction hypothesis, χ(K_{k+1} \setminus \{v\}) = k. Thus, any proper colouring of K_{k+1} must use at least k colours on the vertices other than v. It is not possible to colour v with any of these k colours, since v is adjacent to all of the other vertices, so has a neighbour that is coloured with each of these k colours. Therefore, χ(K_{k+1}) ≥ k + 1. In fact, since v is the only vertex not yet coloured by these k colours, it is clear that k + 1 colours suffice to colour the graph: we colour v with a new colour, which is the k + 1^{\text{st}} colour. This will certainly be a proper colouring of K_{k+1}. Thus, χ(K_{k+1}) = k + 1, completing the induction step.
By the Principle of Mathematical Induction, χ(K_n) = n for every n ≥ 1.
4) The fact that G contains a subgraph isomorphic to K_i implies that χ(G) ≥ i. The fact that ∆(G) ≤ j implies that
χ(G) ≤ ∆(G) + 1 ≤ j + 1.
So, 4 ≤ i ≤ χ(G) ≤ j + 1 ≤ 7.
If we also know that G is connected and is neither a complete graph nor a cycle of odd length, then χ(G) ≤ ∆(G) ≤ j, so 4 ≤ i ≤ χ(G) ≤ j ≤ 6 in this case.
Solutions for Chapter 15
Solutions to Exercise 15.1.1
1) PROOF. Let G be a graph with a nonplanar subgraph H. Suppose (towards a contradiction) that G is planar. Find a planar embedding of G, and delete vertices and/or edges (as appropriate) to reach the subgraph H. No edges that do not share an endvertex have points in common in the embedding of G, and edges that do share an endvertex have no other points in common. This property is not changed by deleting vertices and/or edges, so our result is a planar embedding of H. But this is impossible, since H is nonplanar. The contradiction shows that G must be planar. Since K_5 is a subgraph of K_n for every n ≥ 6 and K_5 is nonplanar by Theorem 15.1.1, this shows that K_n is nonplanar for every n ≥ 6.
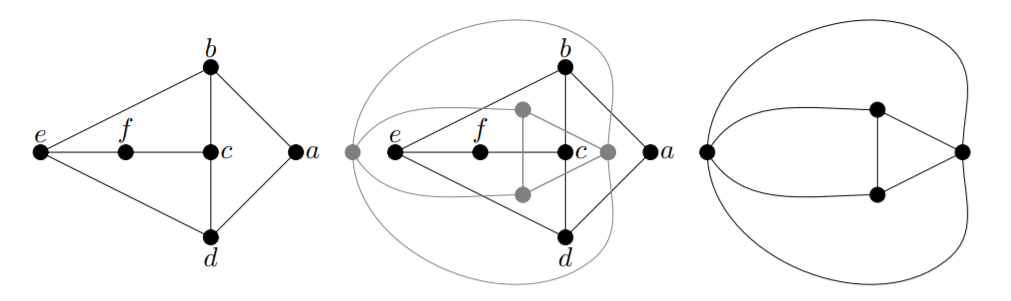
3) We show a planar embedding of the graph, the planar embedding with the dual graph shown in grey, and the dual graph.
Solutions to Exercise 15.2.1
1) We will prove that for any planar embedding of a disconnected planar graph with exactly two connected components, |V| − |E| + |F| = 3.
PROOF. We will prove this formula by induction on the number of faces of the embedding. Let G be a planar embedding of a graph with exactly two connected components.
Base case: If |F| = 1 then G cannot have any cycles (otherwise the interior and exterior of the cycle would be 2 distinct faces). So G must consist of two connected graphs that have no cycles, i.e., two trees, T_1 and T_2. By Theorem 12.4.1 we know that we must have |E(T_1)| = |V (T_1)| − 1 and E(T_2) = V (T_2) − 1, so
V | − |E| + |F| = |V (T_1)| + |V (T_2)| − (|V (T_1)| − 1) − (|V (T_2) − 1) + 1 = 3.
Inductive step: We begin by stating our inductive hypothesis. Let k ≥ 1 be arbitrary, and assume that for any planar embedding of a graph that has exactly two connected components, such that the embedding has k faces, |V| − |E| + |F| = 3.
Let G be a planar embedding of a graph that has exactly two connected components, such that the component has k + 1 ≥ 2 faces. Since forests have only one face, G must have a cycle in at least one of its components. Choose any edge e that is in a cycle of G, and let H = G \setminus \{e\}. Clearly, we have
|E(H)| = |E(G)| − 1
and |V(H)| = |V(G)|. Also,
F(H)| = |F(G)| − 1 = k
since the edge e being part of a cycle must separate two faces of G, which are united into one face of H. Furthermore, since e was in a cycle and G has two connected components, by an argument similar to that given in Proposition 12.3.3 H has two connected components, and H has a planar embedding induced by the planar embedding of G. Therefore our inductive hypothesis applies to H, so
\begin{equation} \begin{split} 2 &= |V (H)| − |E(H)| + |F(H)| \\[0.125in] &= |V (G)| − (|E(G)| − 1) + (|F(G)| − 1) \\[0.125in] &= |V (G)| − |E(G)| + |F(G)| = 3 \end{split} \end{equation}
This completes the inductive step.
By the Principle of Mathematical Induction, |V| − |E| + |F| = 3 for any planar embedding of graph that has exactly two connected components.
4) The value for |V | − |E| + |F| on a torus is 0. For example, consider the graph on 5 vertices consisting of two cycles of length 3 that meet at a vertex. Draw this graph on a torus so that one cycle goes through the hole in the middle, and one cycle goes around the outside edge of the torus. This embedding has one face, since the first cycle cuts the torus into something resembling a cylinder, and the second cuts the cylinder into a rectangle. There are 5 vertices and 6 edges, so |V| − |E| + |F| = 5 − 6 + 1 = 0, as claimed.
Solutions to Exercise 15.3.1
1) First, notice that since G is cubic, every vertex has valency 3, which is odd. Therefore, by Corollary 11.3.1, G must have an even number of vertices. This means that the number of vertices in the Hamilton cycle, and the number of edges in the Hamilton cycle (which are equal) are both even. Thus, we can colour the edges of the Hamilton cycle with 2 colours, say blue and red, alternating between the two colours all the way around the cycle. Since the graph is cubic, each vertex is now incident to exactly one edge that has not yet been coloured. Therefore, we can colour all of the remaining edges with a single colour – green, say. Thus, we have properly 3-edge-coloured G. Since ∆(G) = 3, this means that G is a class one graph.
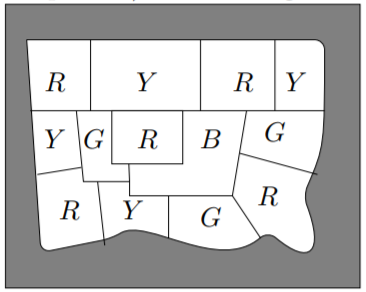
2) We use the letters R, G, B, and Y to represent the four colours. The exterior face (which appears grey in the picture) will be assigned the colour B.
Solutions for Chapter 16
Solutions to Exercise 16.1.1
1) PROOF. Let L be an n×n Latin square whose entries come from a set N of cardinality n, and let L' be the result of exchanging row i with row j.
Let k ∈ \{1, . . . , n\} be arbitrary, and consider column k of L'. Its entries are exactly the same as the entries of column k of L, except that the i^{\text{th}} entry has been exchanged with the j^{\text{th}} entry. Since every element of N appears exactly once in column k of L, it also appears exactly once in column k of L' (although possibly in a different position). Since k was arbitrary, every element of N appears exactly once in each column of L'.
Now consider row k of L'. If k \neq i, j, then this row is exactly the same as row k of L. Since every element of N appears exactly once in row k of L, it also appears exactly once (and in the same position even) in row k of L'. If k = i or k = j, then row k of L' is the same as some other row (the j^{\text{th}} or i^{\text{th}} row, respectively) of L. Since every element of N appears exactly once in that row of L, it also appears exactly once in row k of L'.
Thus, L' satisfies the definition of a Latin square.
2) There are three different ways to complete the square:
1 \; \; 3 \; \; 4\; \; 2\;\;\;\;\; 1 \; \; 3 \; \; 4\; \; 2 \;\;\;\;\; 1 \; \; 3 \; \; 4\; \; 2 \\ 2 \; \; 1 \; \; 3\; \; 4\;\;\;\;\; 3 \; \; 1 \; \; 2\; \; 4 \;\;\;\;\; 3 \; \; 1 \; \; 2\; \; 4 \\ 4 \; \; 2 \; \; 1\; \; 3\;\;\;\;\; 2 \; \; 4 \; \; 1\; \; 3 \;\;\;\;\; 4 \; \; 2 \; \; 1\; \; 3 \\ 3 \; \; 4 \; \; 2\; \; 1\;\;\;\;\; 4 \; \; 2 \; \; 3\; \; 1 \;\;\;\;\; 2 \; \; 4 \; \; 3\; \; 1
So the completion is not unique.
Solutions to Exercise 16.2.1
2) As explained in the first paragraph of the proof of Theorem 16.2.1, we may assume the first row is 1, 2, 3, 4.
Now, we use the idea that is explained in the second paragraph of the proof of Theorem 16.2.1. For any position in a row after the first row, the entry in our new Latin square cannot be the same as the entry in this position of either of the two given squares (because, for any j, the ordered pair (j, j) has already appeared in the top row of the given square and our new square), and it also cannot be the same as the entry in the first row of the column. This eliminates three possibilities for the entry in this position, so there is only one possibility left. Putting this remaining entry into each position yields the following Latin square, which must be the one that was requested:
1 \; \; 2 \; \; 3\; \; 4 \\ 2 \; \; 1 \; \; 4\; \; 3 \\ 3 \; \; 4 \; \; 1\; \; 2 \\ 4 \; \; 3 \; \; 2\; \; 1
3)
1 \; \; 2 \; \; 3\; \; 4\;\;5\;\;6\;\;7\;\;8 \\ 3 \; \; 4 \; \; 1\; \; 2\;\;7\;\;8\;\;5\;\;6 \\ 5 \; \; 6 \; \; 7\; \; 8\;\;1\;\;2\;\;3\;\;4 \\ 7 \; \; 8 \; \; 5\; \; 6\;\;3\;\;4\;\;1\;\;2 \\ 4\;\;3\;\;2\;\;1\;\;8\;\;7\;\;6\;\;5 \\ 2\;\;1\;\;4\;\;3\;\;6\;\;5\;\;8\;\;7 \\ 8\;\;7\;\;6\;\;5\;\;4\;\;3\;\;2\;\;1 \\ 6\;\;5\;\;8\;\;7\;\;2\;\;1\;\;4\;\;3
Solutions to Exercise 16.3.1
2) This collection has no system of distinct representatives, because the five sets A_2, A_3, A_4, A_5, and A_6 have union A_2 ∪ A_3 ∪ A_4 ∪ A_5 ∪ A_6 = \{v, w, x, y\}, which has cardinality 4.
4) This collection does have a system of distinct representatives: x, y, and z, for A_1, A_2, and A_3 (respectively).
Solutions to Exercise 16.3.2
1) Adam, Ella, Jusin, and Bryant are only friends that have visited either England, Scotland, Ireland, France, or Italy. Therefore, she has only 4 friends to choose from to answer the questions for these 5 countries. Since the number of friends is less than the number of countries, she cannot choose a different friend for each of these countries.
2) No, this cannot be completed to a 4 × 4 Latin square:
- The third entry in the third row must be 1, because 2, 3, and 4 already appear in either the third row or the third column.
- The last entry in the third row must also be 1, because 2, 3, and 4 already appear in either the third row or the last column.
So we cannot complete the third row: we are forced to have 1 appear twice in this row, but that is not allowed.
Hall’s Marriage Theorem does not apply to this situation, because, as we have seen, the third column and fourth column must both choose their entry for the third row from the set \{1\}, which has less than two elements. (Theorem 16.3.2 does not apply because the partial Latin square does not consist only of complete rows — it has a row that has only been partially filled in.)
Solutions for Chapter 17
Solutions to Exercise 17.1.1
1) Numerically, this property is easy to verify from the proof of Theorem 17.1.3, which tells us that if b is the number of blocks, then b = \dfrac{λv(v − 1)}{k(k − 1)}, so (dividing both sides by 2 and multiplying through by k(k − 1)) we have b \binom{k}{2} = λ \binom{v}{2}.
The correspondence is due to the colouring explained in Theorem 17.1.2.
2) We are given that v = 16, k = 6, and λ = 3.
From the formula r(k − 1) = λ(v − 1), we see that
r = \dfrac{λ(v − 1)}{k − 1} = \dfrac{3(16 − 1)}{6 − 1}= 9,
which means that each point is in 9 blocks.
Now, from the formula bk = vr, we have
b = \dfrac{vr}{k} = \dfrac{16 · 9}{6} = 24.
This means that the design has 24 blocks.
Solutions to Exercise 17.2.1
1) PROOF. Clearly the complement of a design will still have v varieties. (It will also have b blocks, since each of its blocks comes from one block of the original design.)
From a block B of size k, the corresponding block of the complementary design will have the v − k elements of V \setminus B.
We need to count how many times any given pair of varieties appear together in a block of the complementary design. Two varieties appear together in a block of the complementary design if and only if neither of them was in the corresponding block of the original design. Each of the two varieties appeared in r blocks of the original design, and they appear together in λ blocks of the original design. We can now use inclusion-exclusion to count the number of blocks in which at least one of the two varieties appears: r + r − λ = 2r − λ. Thus, the number of blocks in which neither of them appears is b − (2r − λ) = b − 2r + λ, as claimed. Since this count in no way depended on the choice of our two varieties, the complement is indeed a design, as every pair of varieties appear together in some block b − 2r + λ times.
3) The set \{1, 3, 7\} gives the differences ±2, ±4, and ±6, while the set \{1, 6, 13\} gives the differences ±5, ±7, and ±12. So we need to find two sets that contain the differences ±1, ±3, ±8, ±9, ±10, and ±11. The sets \{1, 2, 11\} and \{1, 4, 12\} work.
Solutions to Exercise 17.3.1
1) Many examples are possible (but they may be hard to find). For example, let
v = 16, k = 6, \text{ and } λ = 1.
Then
λ \dfrac{v − 1}{k − 1} = 1 · \dfrac{16 − 1}{6 − 1} = 3
and
λ \dfrac{v(v − 1)}{k(k − 1)} = 1 · \dfrac{16(16 − 1)}{6(6 − 1)} = \dfrac{16 · 15}{6 · 5} = 8
are integers, so the conditions in Theorem 17.1.2 are satisfied.
From the formula r(k − 1) = λ(v − 1), we see that
r = \dfrac{λ(v − 1)}{k − 1} = 1 · \dfrac{(16 − 1)}{6 − 1} = 3.
Then, from the formula bk = vr, we have
b = \dfrac{vr}{k} = \dfrac{16 · 3}{6} = 8.
Therefore b = 8 < 16 = v, so Fisher’s Inequality is not satisfied.
Since Fisher’s Inequality is not satisfied, there is no BIBD with these parameters.
2) It is shown just before the proof of Fisher’s Inequality that Fisher’s Inequality is equivalent to λ(v − 1) ≥ k(k − 1). Since λ = 1 and k = 20, this means
1 · (v − 1) ≥ 20(20 − 1) = 380,
so v ≥ 380 + 1 = 381. Therefore, v must be at least 381 to satisfy Fisher’s Inequality. Since
λ \dfrac{v − 1}{k − 1} = 1 · \dfrac{381 − 1}{20 − 1} = \dfrac{380}{19} = 20
and
λ \dfrac{v(v − 1)}{k(k − 1)} = 1 · \dfrac{381(381 − 1)}{20(20 − 1)} = \dfrac{381(380)}{380} = 381
are integers, the conditions in Theorem 17.1.2 are also satisfied. So 381 is the smallest value for v that satisfies all three conditions.
Solutions for Chapter 18
Solutions to Exercise 18.1.1
2) Since v = 39 = 6 · 6 + 3 ≡ 3 (\text{mod } 6), the proof of Theorem 18.1.1 tells us that we should use a Latin square constructed in Lemma 18.1.1. Since \dfrac{v}{3} = \dfrac{39}{3} = 13, the Latin square is of order n = 13, so the first sentence of the proof of Lemma 18.1.1 tells us that the first row of the Latin square is
1 \;\;\;\; \dfrac{13 + 3}{2} \;\;\;\; 2 \;\;\;\; \dfrac{13 + 5}{2} \;\;\;\; 3 \;\;\;\; \dfrac{13 + 7}{2} \;\;\;\; 4 \;\;\;\; · · · \;\;\;\; 13 \;\;\;\; \dfrac{13 + 1}{2}..
In other words, the first row is
1 \;\;\;\; 8 \;\;\;\; 2 \;\;\;\; 9 \;\;\;\; 3 \;\;\;\; 10 \;\;\;\; 4 \;\;\;\; 11 \;\;\;\; 5 \;\;\;\; 12 \;\;\;\; 6 \;\;\;\; 13 \;\;\;\; 7.
Then the second sentence of the proof of Lemma 18.1.1 tells us that the rest of the rows are obtained by shifting to the left. So the Latin square is
1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7 \\ 8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1 \\ 2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8 \\ 9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2 \\ 3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9 \\ 10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3 \\ 4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10 \\ 11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4 \\ 5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11 \\ 12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5 \\ 6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12 \\ 13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6 \\ 7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13 \\
4) No, it is not a Kirkman system.
We will call \{u_1, . . . , u_5\} the u-girls; \{v_1, . . . , v_5\} the v-girls; and \{w_1, . . . , w_5\} the w-girls. Of the 35 blocks that we obtained through the construction, 5 have one u-girl, one v-girl, and one w-girl; the other 30 have either two u-girls with a v-girl, two v-girls with a w-girl, or two w-girls with a u-girl.
A Kirkman system requires us to divide the blocks into 7 groups of 5 blocks such that each girl appears exactly once in each group of blocks. Since there should be 7 groups of 5 blocks, but there are only 5 blocks that have a u-girl, a v-girl, and a w-girl, there must be at least one group of blocks (in fact, at least two) that has no block consisting of a u-girl, a v-girl, and a w-girl.
Consider such a group of 5 blocks. We must have all 5 of the u-girls. If no block contained more than one u-girl, then in order to get all 5 u-girls we would have to choose only blocks that have two w-girls and a u-girl. However, this would mean that we had 10 w-girls and no v-girls, which is not allowed. So we must choose at least one block that has two u-girls and a v-girl. Repeating the same argument with v or w taking the place of u, we see that we must also choose at least one block that has two v-girls and a w-girl, and at least one block that has two w-girls and a u-girl. Since we are only choosing 5 blocks but there are these three classes of blocks, there must be some class of blocks of which we only choose one.
Without loss of generality, suppose that we only choose one of the blocks that has two u-girls and a w-girl. In order to have all 5 of the u-girls, we must choose three blocks that have two w-girls and a u-girl. But this means that we have six w-girls, which is not allowed.
Therefore, there is no way to partition the blocks of this design into seven groups of five blocks so that every girl appears exactly once in each group.
Solutions to Exercise 18.2.1
2) We must have b \binom{k}{t} = λ \binom{v}{t} = \binom{15}{t}.
Since we are not including any trivial t−(v, t, 1) design, we have t ≥ 2, 3 ≤ k ≤ 14, and t < k.
Now
\dfrac{15!}{t!(15 − t)!} = b \dfrac{k!}{t!(k − t)!},
which means that
\dfrac{15 · 14 · · ·(16 − t)}{k(k − 1)· · ·(k + 1 − t)}
is an integer.
Furthermore, we have \binom{k − 1}{t − 1} divides \binom{14}{t − 1}, so that \binom{(k − 1)!}{(k − t)!} divides \binom{14!}{(15 − t)!}. In other words,
\dfrac{14!(k − t)!}{(15 − t)!(k − 1)!} = \dfrac{14 · 13 · · ·(16 − t)}{(k − 1)(k − 2)· · ·(k + 1 − t)}
is an integer. If we call this integer y, combining this with the previous paragraph tells us that k is a divisor of 15y. We can also further work with the algebra to obtain
y = \dfrac{14 · 13 · · · k}{(15 − t)(14 − t)· · ·(k + 1 − t)}.
When k = 14, this gives y = \dfrac{14}{(15 − t)}. Since k divides 15y and k is coprime to 15, we must have k divides y. But then \dfrac{y}{14} = \dfrac{1}{(15 − t)} is an integer, implying t = 14. This contradicts t < k. Thus k = 14 cannot arise.
When k = 13 this gives y = \dfrac{14 · 13}{(15 − t)(14 − t)}. Since k divides 15y and k is coprime to 15, we must have k divides y. But then \dfrac{y}{13} = \dfrac{14}{(15 − t)(14 − t)} is an integer. Since t < k = 13, we have 14 − t ≥ 2, but no two consecutive integers each of which is at least 2 are both divisors of 14, a contradiction. Thus k = 13 cannot arise.
When k = 12, this gives
y = \dfrac{14 · 13 · 12}{(15 − t)(14 − t)(13 − t)} .
Now k dividing 15y implies that
\dfrac{15 · 14 · 13}{(15 − t)(14 − t)(13 − t)}
is an integer. Since the numerator is not a multiple of 2^2, the denominator cannot be either, leaving only the possibilities t = 4, 8. Since the numerator is not a multiple of 3^2, the denominator cannot be either, which eliminates t = 4. When t = 8, the numerator of y is not a multiple of 5, but the denominator is, so this is also impossible. Thus k = 12 cannot arise.
When k = 11 this gives
y = \dfrac{14 · 13 · 12 · 11}{(15 − t)(14 − t)(13 − t)(12 − t)} .
Since k divides 15y and k is coprime to 15, we must have k divides y. But then
\dfrac{y}{11} = \dfrac{14 · 13 · 12}{(15 − t)(14 − t)(13 − t)(12 − t)}
is an integer. Since the numerator is not a multiple of 5, the four consecutive numbers that are the factors of the denominator must be 6 through 9 (since t ≥ 2, they cannot be 11 through 14, and since t < 11 they cannot be 1 through 4). Thus, we must have t = 6. But then the numerator is not divisible by 3^2, while the denominator is divisible by 3^3, contradicting \dfrac{y}{11} being an integer. Thus k = 11 is not possible.
When k = 10, this gives
y = \dfrac{14 · 13 · 12 · 11 · 10}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)}.
Now k dividing 15y implies that
\dfrac{15 · 14 · 13 · 12 · 11}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)}
is an integer. Since the numerator is not a multiple of 2^4, the denominator cannot be either. In particular, 8 cannot be one of the factors that appears in the denominator (since some other even factor would appear with it), nor can 2, 4, and 6 all be factors that appear in the denominator. Also, the numerator is not divisible by 3^3, so we cannot have 11 − t = 9. This leaves t = 8 as the only possibility. However, the numerator of y is not divisible by 3^2, so t = 8 is also not possible. Thus k = 10 is not possible.
When k = 9, we see that
y = \dfrac{14 · 13 · 12 · 11 · 10 · 9}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)}.
So k dividing 15y gives
\dfrac{15 · 14 · 13 · 12 · 11 · 10}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)}
being an integer. Since the numerator is not divisible by 2^5, the denominator cannot be either. In particular, 8 cannot appear as one of the factors in the denominator (or two other numbers divisible by 2 would also appear as factors), so the only possibility is t = 8. However, if we take k = 9, t = 8, and i = 2, the necessary condition is 7\binom{7}{6} = 7 divides \binom{13}{6}, which is not true. Thus, k = 9 is not possible.
When k = 8, we calculate
y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)}.
Since k divides 15y and k is coprime to 15, we must have k divides y. But then
\dfrac{y}{8} = \dfrac{14 · 13 · 12 · 11 · 10 · 9}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)}.
Since the consecutive factors in the denominator include 8 and at least two other even numbers, this implies that the numerator should also be a multiple of 2^5, but it is not. Thus k = 8 is not possible.
When k = 7 we see that
y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)}.
Since the consecutive factors in the denominator include 6 and 9, if they also include another multiple of 3 then the numerator must be divisible by 3^4, but it is not. This leaves the possibility that t = 4 so the factors in the denominator are 4 through 11, but this is divisible by 5^2, which the numerator is not. Thus, k = 7 is not possible.
If k = 6 then
y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7 · 6}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)}.
So k dividing 15y gives
\dfrac{15 · 14 · 13 · 12 · 11 · 10 · 9 · 8 · 7}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)}
being an integer. The numerator is not divisible by 2^8, so the denominator cannot be either; in particular it cannot include as factors all of the even integers from 4 through 10 as well as one other. This leaves the possibilities t = 2 and t = 4. If t = 2 then y = \dfrac{14}{5} which is not an integer, and similarly if t = 4 then we have y = \dfrac{14 · 13 · 12}{5 · 4 · 3} which is not an integer. So k = 6 is not possible.
If k = 5 then
y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7 · 6 · 5}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)(6 − t)}.
The numerator is not divisible by 2^9, so the denominator cannot be either; in particular, the denominator cannot include all of 4, 6, 8, 10, and 12 as factors in the product. This leaves only the possibility t = 4. If k = 5 and t = 4 then i = 0 gives \binom{5}{4} = 5 divides \binom{15}{4} = 1365 which is true; i = 1 gives \binom{4}{3} = 4 divides \binom{14}{3} = 364 which is true; i = 2 gives \binom{3}{2} = 3 divides \binom{13}{2} = 78, which is true; i = 3 gives \binom{2}{1} = 2 divides \binom{12}{1} = 12, which is true. Thus a 4−(15, 5, 1) design could exist, but this is the only possibility with k = 5.
When k = 4 we have
y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7 · 6 · 5 · 4}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)(6 − t)(5 − t)}
The denominator includes 3, 6, 9, and 12, so is divisible by 3^5, but the numerator is not. Thus, k = 4 is not possible.
If k = 3 then 2 ≤ t < k implies t = 2. We know these parameters are possible, as these are the parameters of a Steiner triple system.
Thus, the only possible values of k and t ≥ 2 for which nontrivial t-designs might exist with v = 15 and λ = 1 are k = 5 and t = 4: a 4−(15, 5, 1) design, or k = 3 and t = 2: a (15, 3, 1) Steiner triple system.
3) If a 3−(16, 6, 1) design exists then we have bk = vr and b \binom{k}{t} = λ \binom{v}{t}. The second equation gives b \binom{6}{3} = \binom{16}{3}, so b = 28, so it would have 28 blocks. Now bk = vr gives 28 · 6 = 16r. This has no integral solution, so such a design is not possible.
Solutions to Exercise 18.3.1
1) PROOF. Let L, M, and N be lines of an affine plane such that L is parallel to both M and N; that is, no point lies on both L and M or on both L and N. Let p be an arbitrary point on M. Since L and M are parallel, p does not lie on L. By the parallel postulate, there is a unique line through p that is parallel to L; this line is M. Therefore N cannot contain p. Since our choice of p on M was arbitrary, no point of M can also lie on N, so M and N are parallel.
3) A finite affine plane of order 19 has 19^2 = 361 points, and 19(19 + 1) = 380 lines.
5) Without colours it is difficult to effectively draw this plane so that the parallel classes can be clearly seen. We will use solid vertical lines; solid horizontal lines; dashed lines; dotted lines; solid grey lines; and dotted grey lines to represent the six parallel classes of lines, but some of these may be difficult to distinguish. Note that the lines that are neither vertical nor horizontal will “turn corners” or zig-zag to join their sets of 5 points.
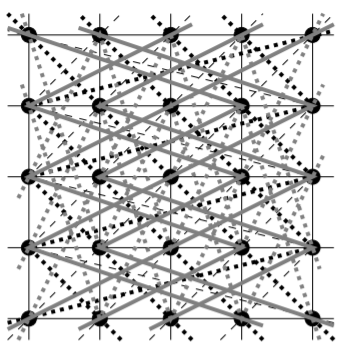
We obtain the following 4 MOLS of order 5 from this affine plane, by using the vertical and horizontal lines to create the coordinates. To make things easier to see, we will have the positions in the Latin squares correspond visually to the positions in the 5 by 5 array of points that we have drawn, so the top-left entry in the Latin squares will come from the top-left point of the array, etc. We will number the lines in each parallel class so as to ensure that the entries in the top row of each square are 1, 2, 3, 4, and 5, in that order. The first square corresponds to the dashed lines; the second to the dotted lines; the third to the solid grey lines, and the fourth to the dashed grey lines.
1\;\;2\;\;3\;\;4\;\;5 \;\;\;\;\; 1\;\;2\;\;3\;\;4\;\;5 \;\;\;\;\; 1\;\;2\;\;3\;\;4\;\;5 \;\;\;\; 1\;\;2\;\;3\;\;4\;\;5 \\ 2\;\;3\;\;4\;\;5\;\;1 \;\;\;\;\; 5\;\;1\;\;2\;\;3\;\;4 \;\;\;\;\; 3\;\;4\;\;5\;\;1\;\;2 \;\;\;\; 4\;\;5\;\;1\;\;2\;\;3 \\ 3\;\;4\;\;5\;\;1\;\;2 \;\;\;\;\; 4\;\;5\;\;1\;\;2\;\;3 \;\;\;\;\; 5\;\;1\;\;2\;\;3\;\;4 \;\;\;\; 2\;\;3\;\;4\;\;5\;\;1 \\ 4\;\;5\;\;1\;\;2\;\;3 \;\;\;\;\; 3\;\;4\;\;5\;\;1\;\;2 \;\;\;\;\; 2\;\;3\;\;4\;\;5\;\;1 \;\;\;\; 5\;\;1\;\;2\;\;3\;\;4 \\ 5\;\;1\;\;2\;\;3\;\;4 \;\;\;\;\; 2\;\;3\;\;4\;\;5\;\;1 \;\;\;\;\; 4\;\;5\;\;1\;\;2\;\;3 \;\;\;\; 3\;\;4\;\;5\;\;1\;\;2
Solutions to Exercise 18.4.1
1) No, not every design with λ = 1 is a projective plane. The condition λ = 1 ensures that every two points have a unique line that is incident with both of them. However, there is no requirement in a design that every two blocks have a nonempty intersection. (If every two blocks do have a nonempty intersection, then the condition λ = 1 does force the intersection to have exactly one point.) The condition that there exist four points such that no three are incident with a single line can also fail, but only in trivial or complete situations.
3) From Theorem 16.2.2, we know that there are p − 1 MOLS of order p whenever p is prime. This implies that there is a projective plane that has p + 1 points on each line whenever p is prime.
4) Since there are not 5 MOLS of order 6 (as we saw in Euler’s problem), there is no projective plane that has 7 points on each line.
Solutions for Chapter 19
Solutions to Exercise 19.1.1
The only string with an odd number of 1s is 10101, so it is not an allowable message, but all of the others are allowed.
Solutions to Exercise 19.2.2
1) The only such word is “math.”
3) There are many possibilities, such as “\text{\(\underline{\text{b}}\)at\(\underline{\text{s}}\)},” “\text{\(\underline{\text{g}}\)a\(\underline{\text{s}}\)h},” and “\text{ma\(\underline{\text{n}}\)\(\underline{\text{y}}\)}.”
5) We have answered this in each solution given above.
Solutions to Exercise 19.2.3
2) PROOF. Let x and y be words of the same length. We have d(x, y) = 0 if and only if x and y differ in no positions. This means that x must have the same entry as y in every position, which means x = y.
4) PROOF. Let x, y, and z be words of the same length. Suppose that d(x, z) = k, so that x and z differ in k positions. Suppose that d(x, y) = i, so y differs from x in i positions. If i ≥ k then since d(y, z) ≥ 0 by part (1), we have d(x, z) ≤ d(x, y)+d(y, z). Otherwise, there must be some list of at least k − i positions in which x differs from z but does not differ from y. In each of these positions, since y has the same entry as x, y must have a different entry than z. Therefore d(y, z) ≥ k −i. Now d(x, y) +d(y, z) ≥ i + k − i = k = d(x, z), completing the proof.
Solutions to Exercise 19.2.4
3) The minimum distance is 2. To see this, first note that d(01011, 10011) = 2, so the minimum distance is no more than 2. Since each of the nonzero codewords has exactly three 1s, its distance from 00000 is 3, and its distance to any other nonzero codeword is greater than 1 because changing a single bit will change the number of 1’s. So the minimum distance is at least 2.
Solutions to Exercise 19.2.5
2) (a) The code can detect 5 errors, but not 6 (because the number of errors detected must be less than the minimum distance).
(b) The code can correct 2 errors (because 2 × 2 < 6, but 2 × 3 \nless 6).
Solutions to Exercise 19.3.1
1) Since
G = \left[ \begin{array}{ll} I_k \\ A \end{array} \right] = \left[ \begin{array}{ll} 1\;\;0\;\;0\;\;0 \\ 0\;\;1\;\;0\;\;0 \\ 0\;\;0\;\;1\;\;0 \\ 0\;\;0\;\;0\;\;1 \\ 1\;\;1\;\;0\;\;0 \\ 1\;\;0\;\;0\;\;1 \end{array} \right]
we have
G = \left[ \begin{array}{ll} 0 \\ 1 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \end{array} \right], \;\;\;\;\;\;\;\; G = \left[ \begin{array}{ll} 0 \\ 0 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right], \;\;\;\;\;\;\;\; G = \left[ \begin{array}{ll} 1 \\ 1 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array}{ll} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{array} \right]
This means that 0101 encodes as 010111, 0010 encodes as 001000, and 0010 encodes as 111001.
Solutions to Exercise 19.4.2
Since G = \left[ \begin{array}{ll} I_k \\ A \end{array} \right], and the given matrix G has 4 columns, we must have k = 4, so I_k = I_4 has 4 rows. Therefore, A is all but the first 4 rows of G, which means
A = \left[ \begin{array}{ll} 1\;\;0\;\;1\;\;1 \\ 1\;\;0\;\;0\;\;1 \\ 0\;\;1\;\;1\;\;1 \end{array} \right]
Since A is a 3 × 4, matrix, we have r = 3, so the parity-check matrix is
P = [A \;\; I_r] = [A \;\; I_3] = \left[ \begin{array}{ll} 1\;\;0\;\;1\;\;1\;\;1\;\;0\;\;0 \\ 1\;\;0\;\;0\;\;1\;\;0\;\;1\;\;0 \\ 0\;\;1\;\;1\;\;1\;\;0\;\;0\;\;1 \end{array} \right]
Solutions to Exercise 19.4.4
2) (a) Yes, all six columns of the parity-check matrix are different from each other (and none of them are all 0), so Theorem 19.4.1 tells us that the code can correct all single-bit errors.
(b) Let P be the given parity-check matrix. Then:
- G = \left[ \begin{array}{ll} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 1 \\ 0 \end{array} \right].\;\;\;\; This is the 5^{\text{th}} column of P, so changing the 5^{\text{th}} bit corrects the error. The received word 001001 decodes as 0010 \underline{1} 1.
- G = \left[ \begin{array}{ll} 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 0 \\ 0 \end{array} \right].\;\;\;\; This is 0, so there is no error. The received word 110011 decodes as 110011.
- G = \left[ \begin{array}{ll} 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array}{ll} 1 \\ 1 \\ 0 \end{array} \right].\;\;\;\; This is the 2^{\text{nd}} column of P, so changing the 2^{\text{nd}} bit corrects the error. The received word 000110 decodes as 0 \underline{1} 0110.
Solutions to Exercise 19.4.5
1) There are 2^5 − 1 = 31 different nonzero 5-bit strings. Of these 31 strings, 5 of them have only one 1. Thus, there are 31 − 5 = 26 different nonzero strings with at least two 1s. Therefore, we can make a 5 × 24 matrix A, such that the columns of A are 24 different binary column vectors with at least two 1s in each column (because there are 26 different possible columns to choose from, and we need only 24 of them). The columns of the resulting parity-check matrix P = [A \;\;I_5] are all nonzero and distinct, so Theorem 19.4.1 tells us that the resulting binary linear code can correct every single-digit error.
Furthermore, since P is 5 × 24, we know that r = 5 and k = 24. Since r = n − k, this implies n = k+r = 24+ 5 = 29. So the code is of type (n, k) = (29, 24), as desired.
3) Suppose P is the parity-check matrix of a binary linear code of type (n, k) that corrects all single-bit errors, and let r = n − k. Then Theorem 19.4.1 tells us that the columns of P must be distinct (and nonzero). However, P is r × n, and n = k + r, so it has k + r columns of length r, and there are only 2^r − 1 different possible nonzero columns of length r. Therefore, we must have k + r ≤ 2^r − 1. Conversely, if this inequality is satisfied, then we can construct a k × (k + r) parity-check matrix whose columns are all distinct and nonzero. Thus, the smallest possible number of check bits is the smallest value of r that satisfies the inequality k + r ≤ 2^r − 1.
Thus:
- r = 2 check bits suffice for k = 1, because k + r = 1 + 2 = 3 = 2^2 − 1 = 2^r − 1. (But r = 1 check bit does not suffice, because k +r ≥ 1 + 1 = 2 > 2^1 −1 = 2^r −1).
- r = 3 check bits suffice for k = 2, 3, 4, because k +r ≤ 4 + 3 = 7 = 2^3 −1 = 2^r −1. (But r = 2 check bits do not suffice, because k + r ≥ 2 + 2 = 4 > 2^2 − 1 = 2^r − 1).
- r = 4 check bits suffice for 5 ≤ k ≤ 11, because k+r ≤ 11+4 = 15 = 2^4−1 = 2^r−1. (But r = 3 check bits do not suffice, because k + r ≥ 5 + 3 = 8 > 2^3 − 1 = 2^r − 1).
- r = 5 check bits suffice for 12 ≤ k ≤ 20, because k + r ≤ 20 + 5 = 25 < 31 = 2^5 − 1 = 2^r − 1. (But r = 4 check bits do not suffice, because k+r ≥ 12+4 = 16 > 2^4−1 = 2^r −1).
Solutions to Exercise 19.5.1
1) Using Proposition 19.5.1, we have v = 10, k − 2 = 4 so that k = 6, and λ = 1. The question is asking us for b. Using bk(k − 1) = λv(v − 1) gives 30b = 90 so b = 3. Such a code will have only 3 words.


