3.E: Generating Functions (Exercises)
- Page ID
- 7241
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)3.2: Newton's Binomial Theorem
For some of these exercises, you may want to use the sage applet above, in Example 3.2.3, or your favorite computer algebra system.
Prove that \({r\choose k}={r-1\choose k-1}+{r-1\choose k}\).
Show that the Maclaurin series for \((x+1)^r\) is \(\sum_{i=0}^\infty {r\choose i}x^i\).
Concerning Example 3.2.3, show that all coefficients beginning with \(x^{16}\) are 180.
Use a generating function to find the number of solutions to \( x_1+x_2+x_3+x_4=14\), where \(0\le x_1\le3\), \(2\le x_2\le5\), \(0\le x_3\le5\), \(4\le x_4\le6\).
Find the generating function for the number of solutions to \( x_1+x_2+x_3+x_4=k\), where \(0\le x_1\le\infty\), \(3\le x_2\le\infty\), \(2\le x_3\le5\), \(1\le x_4\le5\).
Find a generating function for the number of non-negative integer solutions to \(3x+2y+7z=n\).
Suppose we have a large supply of red, white, and blue balloons. How many different bunches of 10 balloons are there, if each bunch must have at least one balloon of each color and the number of white balls must be even?
Use generating functions to show that every positive integer can be written in exactly one way as a sum of distinct powers of 2.
Suppose we have a large supply of blue and green candles, and one gold candle. How many collections of \(n\) candles are there in which the number of blue candles is even, the number of green candles is any number, and the number of gold candles is at most one?
3.3: Exponential Generating Functions
Find the coefficient of \(x^9/9!\) in the function of Example 3.3.1. You may use Sage or a similar program.
# Enter your function here (e^x shown as an example):
f=exp(x)
# Now we compute the first few terms of the Taylor series,
# extract the coefficients, and multiply by the factorial to
# get the part of the coefficients we want.
g=f.taylor(x,0,13)
L=g.coefficients()
coeffs={c[1]:c[0]*factorial(c[1]) for c in L}
# coeffs is now a "dictionary" that holds pairs n:m, where
# n is the exponent and m is the coefficient. Note that
# coefficients with value zero are not included.
coeffs
Find an exponential generating function for the number of permutations with repetition of length \(n\) of the set \(\{a,b,c\}\), in which there are an odd number of \(a\,\)s, an even number of \(b\,\)s, and an even number of \(c\,\)s.
Find an exponential generating function for the number of permutations with repetition of length \(n\) of the set \(\{a,b,c\}\), in which the number of \(a\,\)s is even and at least 2, the number of \(b\,\)s is even and at most 6, and the number of \(c\,\)s is at least 3.
In how many ways can we paint the 10 rooms of a hotel if at most three can be painted red, at most 2 painted green, at most 1 painted white, and any number can be painted blue or orange?
Recall from Section 1.5 that the Bell numbers \(B_n\) count all of the partitions of \(\{1,2,\ldots,n\}\).
Let \( f(x)=\sum_{n=0}^\infty B_n\cdot {x^n\over n!}\), and note that \[ f'(x)=\sum_{n=1}^\infty B_n {x^{n-1}\over (n-1)!}= \sum_{n=0}^\infty B_{n+1}{x^{n}\over n!}= \sum_{n=0}^\infty \left(\sum_{k=0}^n {n\choose k}B_{n-k}\right) {x^{n}\over n!}, \nonumber\] using the recurrence relation Equation 1.5.1 for \(B_{n+1}\) from Section 1.5. Now it is possible to write this as a product of two infinite series: \[ f'(x) = \left(\sum_{n=0}^\infty B_n\cdot {x^n\over n!}\right) \left(\sum_{n=0}^\infty a_n x^n\right) = f(x)g(x). \nonumber\] Find an expression for \(a_n\) that makes this true, which will tell you what \(g(x)\) is, then solve the differential equation for \(f(x)\), the exponential generating function for the Bell numbers. From Section 1.5, the first few Bell numbers are 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437. You can check your answer in Sage.
# Enter your function here (e^x shown as an example):
f=exp(x)
# Now we compute the first few terms of the Taylor series,
# extract the coefficients, and multiply by the factorial to
# get the part of the coefficients we want.
g=f.taylor(x,0,13)
L=g.coefficients()
coeffs={c[1]:c[0]*factorial(c[1]) for c in L}
# coeffs is now a "dictionary" that holds pairs n:m, where
# n is the exponent and m is the coefficient. Note that
# coefficients with value zero are not included.
coeffs
3.4: Partitions of Integers
Use generating functions to find \(p_{15}\).
Find the generating function for the number of partitions of an integer into distinct odd parts. Find the number of such partitions of 20.
Find the generating function for the number of partitions of an integer into distinct even parts. Find the number of such partitions of 30.
Find the number of partitions of 25 into odd parts.
Find the generating function for the number of partitions of an integer into \(k\) parts; that is, the coefficient of \(x^n\) is the number of partitions of \(n\) into \(k\) parts.
Complete row 8 of the table for the \(p_k(n)\), and verify that the row sum is 22, as we saw in Example 3.4.2.
A partition of \(n\) is self-conjugate if its Ferrers diagram is symmetric around the main diagonal, so that its conjugate is itself. Show that the number of self-conjugate partitions of \(n\) is equal to the number of partitions of \(n\) into distinct odd parts.
3.5: Recurrence Relations
Find the generating function for the solutions to \(h_n=4h_{n-1}-3h_{n-2}\), \(h_0=2\), \(h_1=5\), and use it to find a formula for \(h_n\).
Find the generating function for the solutions to \(h_n=3h_{n-1}+4h_{n-2}\), \(h_0=h_1=1\), and use it to find a formula for \(h_n\).
Find the generating function for the solutions to \(h_n=2h_{n-1}+3^n\), \(h_0=0\), and use it to find a formula for \(h_n\).
Find the generating function for the solutions to \(h_n=4h_{n-2}\), \(h_0=0\), \(h_1=1\), and use it to find a formula for \(h_n\). (It is easy to discover this formula directly; the point here is to see that the generating function approach gives the correct answer.)
Find the generating function for the solutions to \(h_n=h_{n-1}+h_{n-2}\), \(h_0=1\), \(h_1=3\), and use it to find a formula for \(h_n\).
Find the generating function for the solutions to \(h_n=9h_{n-1}-26h_{n-2}+24h_{n-3}\), \(h_0=0\), \(h_1=1\), \(h_2=-1\), and use it to find a formula for \(h_n\).
Find the generating function for the solutions to \(h_n=3h_{n-1}+4h_{n-2}\), \(h_0=0\), \(h_1=1\), and use it to find a formula for \(h_n\).
Find a recursion for the number of ways to place flags on an \(n\) foot pole, where we have red flags that are 2 feet high, blue flags that are 1 foot high, and yellow flags that are 1 foot high; the heights of the flags must add up to \(n\). Solve the recursion.
In Fibonacci's original problem, a farmer started with one (newborn) pair of rabbits at month 0. After each pair of rabbits was one month old, they produced another pair each month in perpetuity. Thus, after 1 month, he had the original pair, after two months 2 pairs, three months, 3 pairs, four months, 5 pairs, etc. The number of pairs of rabbits satisfies \(h_n=h_{n-1}+h_{n-2}\), \(h_0=h_1=1\). (Note that this is slightly different than our definition, in which \(h_0=0\).)
Suppose instead that each mature pair gives birth to two pairs of rabbits. The sequence for the number of pairs of rabbits now starts out \(h_0=1\), \(h_1=1\), \(h_2=3\), \(h_3=5\), \(h_4=11\). Set up and solve a recurrence relation for the number of pairs of rabbits. Show also that the sequence satisfies \(h_n=2h_{n-1}+(-1)^n\).
3.6: Catalan Numbers
Show that \[ {2n\choose n}-{2n\choose n+1}={1\over n+1}{2n\choose n}. \nonumber\]
Find a simple expression \(f(n)\) so that \(C_{n+1}=f(n)C_n\). Use this to compute \(C_1,\ldots,C_6\) from \(C_0\).
Show that if \(A_n\) is the number of properly matched sequences of parentheses of length \(2n\), then \[ A_n=\sum_{i=0}^{n-1} A_iA_{n-i-1}. \nonumber\] Do this in the same style that we used for the number of rooted binary trees: Given all the sequences of shorter length, explain how to combine them to produce the sequences of length \(2n\), in such a way that the sum clearly counts the number of sequences. Hint: Prove the following lemma: If \(s\) is a properly matched sequence of parentheses of length \(2n\), \(s\) may be written uniquely in the form \((s_1)s_2\), where \(s_1\) and \(s_2\) are properly matched sequences of parentheses whose lengths add to \(2n-2\). For example, \((())()= ([()])[()]\) and \(()(())=([\,])[(())]\), with the sequences \(s_1\) and \(s_2\) indicated by \([\,]\). Note that \(s_1\) and \(s_2\) are allowed to be empty sequences, with length 0.
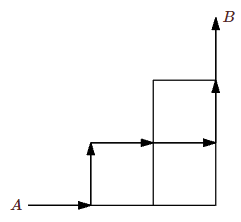
Consider a "staircase'' as shown below. A path from \(A\) to \(B\) consists of a sequence of edges starting at \(A\), ending at \(B\), and proceeding only up or right; all paths are of length 6. One such path is indicated by arrows. The staircase shown is a "\(3 \times 3\)'' staircase. How many paths are there in an \(n\times n\) staircase?
A convex polygon with \(n\ge3\) sides can be divided into triangles by inserting \(n-3\) non-intersecting diagonals. In how many different ways can this be done? The possibilities for \(n=5\) are shown.

A partition of a set \(S\) is a collection of non-empty subsets \(A_i\subseteq S\), \(1\le i\le k\) (the parts of the partition), such that \(\bigcup_{i=1}^k A_i=S\) and for every \(i\not=j\), \(A_i\cap A_j=\emptyset\). For example, one partition of \(\{1,2,3,4,5\}\) is \(\{\{1,3\}\), \(\{4\}\), \(\{2,5\}\}\).
Suppose the integers \(1,2,\ldots,n\) are arranged on a circle, in order around the circle. A partition of \(\{1,2,\ldots,n\}\) is a non-crossing partition if it satisfies this additional property: If \(w\) and \(x\) are in some part \(A_i\), and \(y\) and \(z\) are in a different part \(A_j\), then the line joining \(w\) to \(x\) does not cross the line joining \(y\) to \(z\). The partition above, \(\{1,3\}\), \(\{4\}\), \(\{2,5\}\), is not a non-crossing partition, as the the line 1–3 crosses the line 2–5.
Find the number of non-crossing partitions of \(\{1,2,\ldots,n\}\).
Recall from Section 1.5 that the Bell numbers count all of the partitions of \(\{1,2,\ldots,n\}\). Hence, this exercise gives us a lower bound on the total number of partitions.
Consider a set of \(2n\) people sitting around a table. In how many ways can we arrange for each person to shake hands with another person at the table such that no two handshakes cross?


