4.2: Manipulating quantified statements

4.2.1 Negation of quantified statements

Negating quantified statements in English can be tricky, but we will establish rules that make it easy in symbolic logic.

Warning \(\PageIndex{1}\)

The negation of the statement “all X are Y” is not “no X are Y” nor “all X are not Y”.

Example \(\PageIndex{1}\)

What is the negation of the statement “all cows eat grass”? To avoid making the mistake in the preceding warning, consider the following question: what is the minimum number of cows that do not eat grass that can be used as evidence to demonstrate that the statement “all cows eat grass” is false?

Figure \(\PageIndex{1}\): In this case, both “all cows eat grass” and “some cows eat grass” are true.

Figure \(\PageIndex{2}\): In this case, both “some cows eat grass” and “some cows do not eat grass” are true.

Figure \(\PageIndex{3}\): In this case, each of “no cows eat grass”, “all cows do not eat grass”, and “some cows do not eat grass” are true.

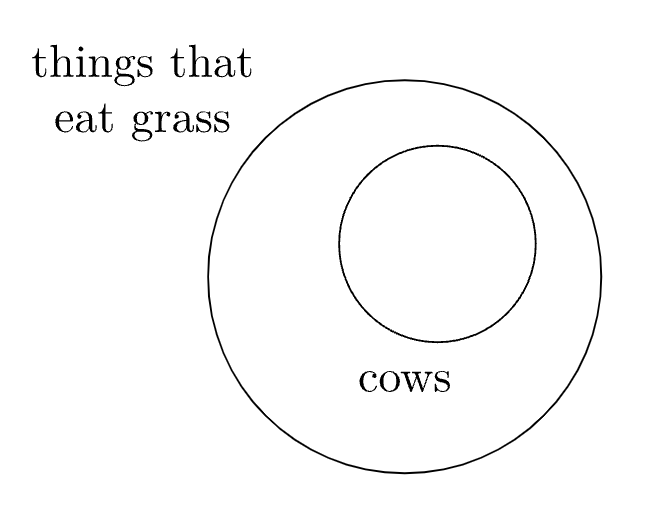
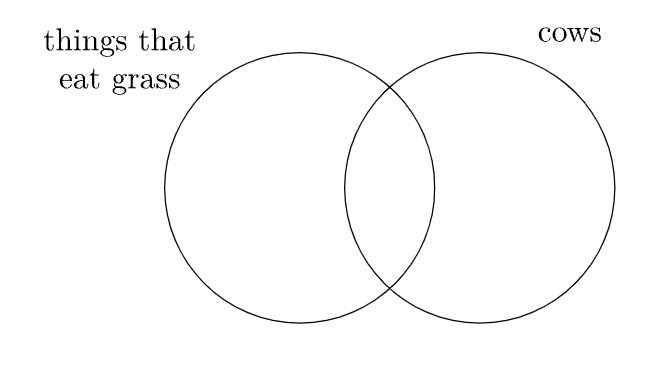
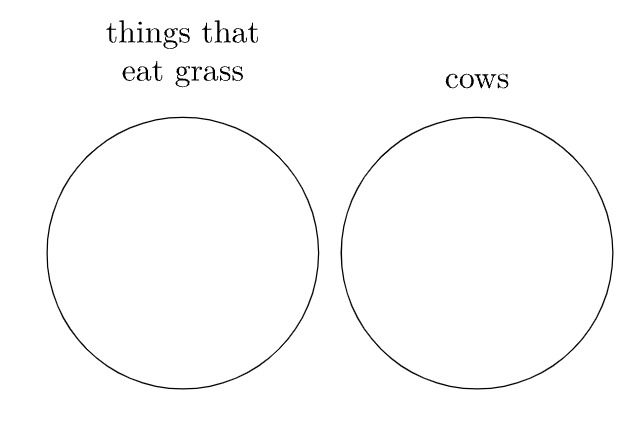
It takes just one lasagna-eating cow to make “all cows eat grass” false, so the negation of “all cows eat grass” is “some cows do not eat grass” or “at least one cow does not eat grass”.

Warning \(\PageIndex{2}\)

We have indicated that the statement “some cows eat grass” is technically true in the first diagram in Example \(\PageIndex{1}\), even though it is more precise to say “all cows eat grass” in that situation. Similarly, we have indicated that the statement “some cows do not eat grass” is technically true in the third diagram. Remember that truth and falsity are usually all that matter in logic, not necessarily making the most precise statement possible.

Proposition \(\PageIndex{1}\): Rules for negation of quantifiers

Let \(A(x)\) represent a predicate in the variable \(x\text{.}\)

1. Universal negation.

The negation of \((\forall x)A(x)\) is \((\exists x)(\neg A(x))\text{.}\)

2. Existential negation.

The negation of \((\exists x)A(x)\) is \((\forall x)(\neg A(x))\text{.}\)

Check your understanding.

Use the “cows eat grass” diagrams in Example \(\PageIndex{1}\) to convince yourself that these negation rules are correct.

Example \(\PageIndex{2}\): Negating a quantified statement

Determine and “simplify” the negation of

\begin{equation*} (\forall x)\left( A(x) \rightarrow \{ (\exists y)(\forall z)\{ B(y)\land \neg C(z) \} \} \right)\text{.} \end{equation*}

Solution

Using the rules of quantifier negation and known logical equivalences, we can perform the following manipulations:

\begin{align*} & \neg (\forall x) \{ A(x) \rightarrow (\exists y)(\forall z)\{ B(y)\land \neg C(z) \} \}\\ &\Leftrightarrow (\exists x) \neg \{ A(x) \rightarrow (\exists y)(\forall z)\{ B(y)\land \neg C(z) \} \} & & \text{(i)}\\ &\Leftrightarrow (\exists x) \neg \{ \neg A(x) \lor (\exists y)(\forall z)\{ B(y)\land \neg C(z) \} \} & & \text{(ii)}\\ &\Leftrightarrow (\exists x) \{ A(x) \land \neg (\exists y)(\forall z) \{ B(y)\land \neg C(z) \} \} & & \text{(iii)}\\ &\Leftrightarrow (\exists x) \{ A(x) \land (\forall y)\neg (\forall z)\{ B(y)\land \neg C(z) \} \} & & \text{(iv)}\\ &\Leftrightarrow (\exists x) \{ A(x) \land (\forall y)(\exists z) \neg \{ B(y)\land \neg C(z) \} \} & & \text{(v)}\\ &\Leftrightarrow (\exists x) \{ A(x) \land (\forall y)(\exists z)\{ \neg B(y)\lor C(z) \} \} & & \text{(vi)} \end{align*}
with justifications

1. quantifier negation;
2. known equivalence \(p\rightarrow q \Leftrightarrow \neg p \lor q\text{;}\)
3. DeMorgan, double negation;
4. quantifier negation;
5. quantifier negation; and
6. DeMorgan, double negation.

4.2.2 Distributing quantifiers

Proposition \(\PageIndex{2}\): Rules for distributing quantifiers

Let \(A(x),B(x)\) represent predicates in the variable \(x\text{.}\)

1. \(\displaystyle (\forall x)\{A(x) \land B(x)\} \Leftrightarrow (\forall x)A(x) \land (\forall x)B(x)\)
2. \(\displaystyle (\exists x)\{A(x) \lor B(x)\} \Leftrightarrow (\exists x)A(x) \lor (\exists x)B(x)\)

Example \(\PageIndex{3}\)

• The statement “every vegetable is delicious and nutritious” is the same as saying “every vegetable is delicious and every vegetable is nutritious”.
• The statement “at least one vegetable in the garden is rotten or nibbled by squirrels” is the same as saying “at least one vegetable in the garden is rotten or at least one vegetable in the garden is nibbled by squirrels”.​

Warning \(\PageIndex{3}\)

• The universal quantifier \(\forall\) does not distribute over disjunction \(\lor\text{.}\)
• The existential quantifier \(\exists\) does not distribute over conjunction \(\land\text{.}\)

Check your understanding.

1. Create an example of predicates \(A(x)\) and \(B(x)\) such that, of the statements

   \begin{align*} (\forall x) & \{A(x) \lor B(x) \} \text{,} & (\forall x) A(x) & \lor (\forall x)B(x) \text{,} \end{align*}

   the first is true but the second is false.
2. Create an example of predicates \(A(x)\) and \(B(x)\) such that, of the statements

   \begin{align*} (\exists x) & \{A(x) \land B(x)\} \text{,} & (\exists x) A(x) & \land (\exists x)B(x) \text{,} \end{align*}

   the first is false but the second is true.