14.6: Exercises

Last updated
Save as PDF

Page ID: 93224

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Exercise \(\PageIndex{1}\)

Consider the graph in Figure 14.6.1.

Figure \(\PageIndex{1}\): An example graph.

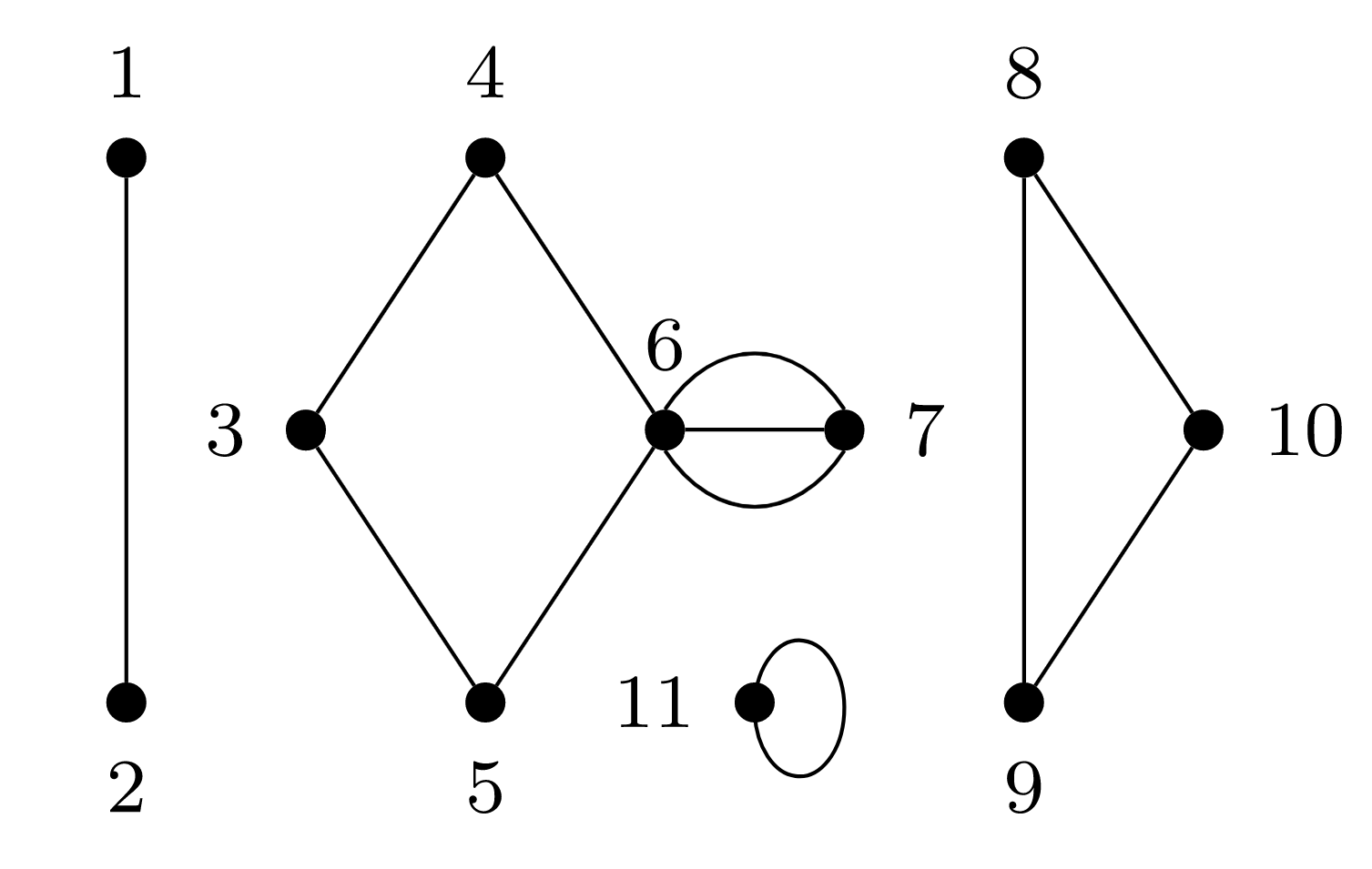
Are vertices 1 and 2 incident?
Are any vertices adjacent to themselves?
Is vertex 3 adjacent to vertex 6?
Is this a simple graph?
Compute the degree of each vertex in the graph. Then verify that the sum of the degrees is equal to twice the number of edges. (See Theorem 14.2.1.)

Exercise \(\PageIndex{2}\)

How many edges does the complete graph with ten vertices have?

Hint.: See Theorem 14.2.1.

Generalize your result to a formula for the number of edges in the complete graph with \(n\) vertices.

Exercise \(\PageIndex{3}\)

Draw an example of a simple graph that has no vertices of odd degree.
Draw an example of a simple graph that has no vertices of even degree.

Exercise \(\PageIndex{4}\)

Given a collection of sets \(A_1,A_2,\ldots,A_n\text{,}\) the intersection graph of the collection is the simple graph that has a vertex for each of the sets in the collection, with two vertices joined by an edge if and only if the two corresponding sets have nonempty intersection. Draw the intersection graph of the following collection of sets.

\begin{gather*} A_1 = \{1,2,3,4,5\}, \\ A_2 = \{2,4,6,8\}, \\ A_3 = \{3,5,12\}, \\ A_4 = \{5,8,10\}. \end{gather*}

Complement of a graph.

Exercises 5–7 concern the following definition.

Definition: Complement(of a simple graph \(G\))

the simple graph that has the same vertex set as \(G\text{,}\) but in which two vertices are joined by an edge if and only if those same two vertices are not joined by an edge in \(G\)

Exercise \(\PageIndex{5}\)

Draw the complement of the simple graph in Figure \(\PageIndex{2}\).

Figure \(\PageIndex{2}\): A simple graph.

Exercise \(\PageIndex{6}\)

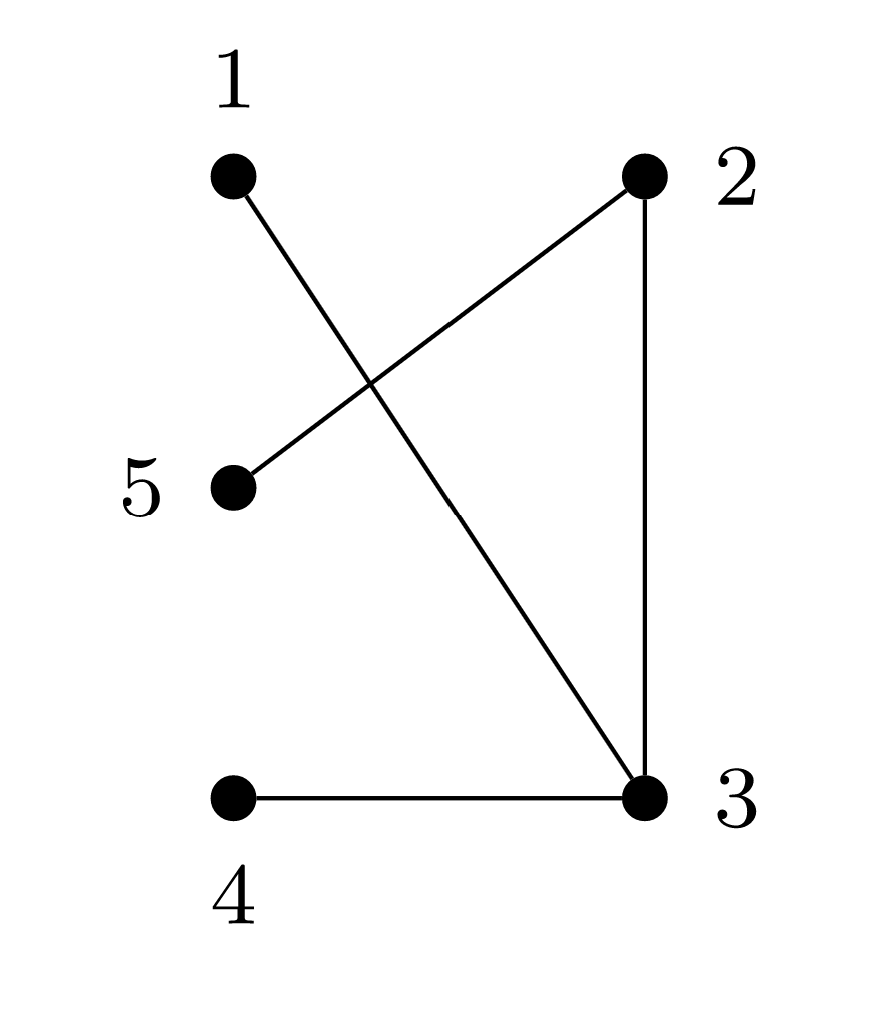
What is the complement of a complete graph?

Exercise \(\PageIndex{7}\)

Suppose \(G\) is a simple graph with \(n\) vertices. Determine a relationship between the number of edges in \(G\text{,}\) the number of edges in the complement of \(G\text{,}\) and the number of edges in the complete graph \(K_n\) with \(n\) vertices.

Hint.: Recall that every simple graph with \(n\) vertices is a subgraph of \(K_n\text{.}\)