15.5: Activities

Activity $\PageIndex{1}$

In each of the following, devise a graph that contains the requested type of walk. (You do not need to create one graph that contains all three types of walks; you may draw three separate graphs.)

1. A closed path that is not a trail.
2. An open trail that is not a path.
3. A closed trail that is not a path.

Activity $\PageIndex{2}$

Devise a graph with exactly four vertices, each of which has degree $5\text{,}$ so that the graph is

1. nonconnected.
2. connected.

Activity $\PageIndex{3}$

In each of the following, devise a connected graph with at least five vertices that has the requested properties. Do so without looking at the example graphs in this chapter. (You do not need to create one graph that contains all of the properties; you may draw a separate graph for each task below.)

1. Contains a bridge.
2. Every edge is a bridge.
3. Contains an articulation vertex.
4. Every vertex of degree at least $2$ is an articulation vertex.

Activity $\PageIndex{4}$

Does increasing the number of edges in a graph increase its edge connectivity?

Activity $\PageIndex{5}$

Figure $\PageIndex{1}$: A nonconnected graph.

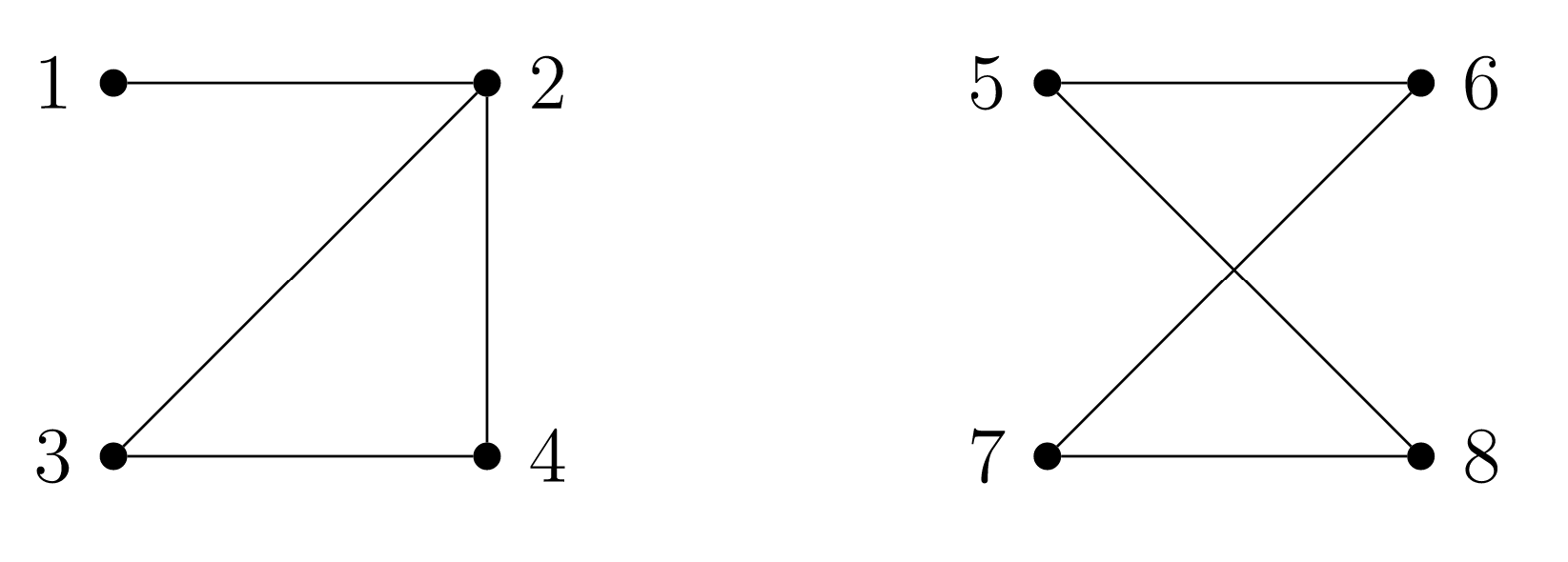
In the graph of Figure $\PageIndex{1}$, explain why the subgraph formed by vertices $2\text{,}$ $3\text{,}$ and $4\text{,}$ along with all edges incident to these vertices, fails the formal definition of connected component. Identify which of the two conditions of this formal definition the subgraph fails, and explicitly describe how the subgraph fails to meet that condition.

Activity $\PageIndex{6}$

Suppose $G$ is a simple, nonconnected graph with $n$ vertices that is maximal with respect to these properties. That is, if you tried to make a larger graph in which $G$ is a subgraph, this larger graph will lose at least one of the properties (a) simple, (b) nonconnected, or (c) has $n$ vertices.

What does being maximal with respect to these properties imply about $G\text{?}$ That is, what further properties must $G$ possess because of this assumption?

Activity $\PageIndex{7}$

An Euler circuit is a closed trail in a connected graph G that traverses every edge of G. Since it must be a trail, you could say that an Euler circuit traverses each edge of G exactly once (as well as ending at the same node at which it begins).

Prove that if a connected graph contains an Euler circuit, then every vertex in that graph must have even degree.