18.3: Classes, partitions, and quotients

As desired (see Section 18.1), an equivalence relation can be used to group equivalent objects together.

Example \(\PageIndex{1}\)

Consider \(\mathord{\equiv_5}\) on \(\mathbb{N}\text{.}\) Notice that the elements in each of the following sets are all equivalent to each other with respect to \(\mathord{\equiv_5}\text{.}\)

\begin{gather*} \{ 0, 5, 10, 15, \ldots \} \\ \{ 1, 6, 11, 16, \ldots \} \\ \{ 2, 7, 12, 17, \ldots \} \\ \{ 3, 8, 13, 18, \ldots \} \\ \{ 4, 9, 14, 19, \ldots \} \end{gather*}
Also notice that \(\mathbb{N}\) is the disjoint union of the above sets.

In fact, we could do the same for every divisor \(n\text{,}\) not just for \(n = 5\text{,}\) as \(\mathbb{N}\) is also the disjoint union of the sets

\begin{gather*} \{ \, 0, \, n, \, 2n, \, 3n, \, \ldots \, \}, \\ \{ \, 1, \, n+1, \, 2n+1, \, 3n+1, \, \ldots \, \}, \\ \{ \, 2, \, n+2,\, 2n+2,\, 3n+2, \, \ldots \, \}, \\ \vdots \\ \{ \, n-1, \, n + (n-1), \, 2n + (n-1), \, 3n + (n-1), \, \ldots \, \}, \end{gather*}
and again elements in each of the above sets are all equivalent to each other with respect to \(\mathord{\equiv_n}\text{.}\)

Definition: equivalence class (of an element \(a\))

the subset of \(A\) consisting of all elements that are equivalent to the given element \(a \in A\text{,}\) relative to a specific equivalence relation \(\mathord{\equiv}\) on \(A\text{;}\) i.e. the set

\begin{equation*} \{ x\in A \vert x \equiv a \} \end{equation*}

Definition: \([a]\)

the equivalence class of the element \(a \in A\) relative to some specific equivalence relation on \(A\)

Example \(\PageIndex{2}\): Equivalence classes of natural numbers modulo \(5\).

If we divide \(8\) by \(5\text{,}\) we get \(1\) with \(3\) remainder. So the equivalence class of \(8\) relative to \(\mathord{\equiv_5}\) consists of all natural numbers that have remainder \(3\) when divided by \(5\text{:}\)

\begin{equation*} [8] = \{ 3, 8, 13, 18, \ldots \} \text{.} \end{equation*}
Now, \(3\) is in this class because when we divide \(3\) by \(5\) we get \(0\) with \(3\) remainder. But if we had started with \(3\) instead of \(8\text{,}\) we would have also said that the equivalence class of \(3\) relative to \(\mathord{\equiv_5}\) consists of all natural numbers that have remainder \(3\) when divided by \(5\text{:}\)

\begin{equation*} [3] = \{ 3, 8, 13, 18, \ldots \} \text{.} \end{equation*}

Proposition \(\PageIndex{1}\): Properties of equivalence classes.

Suppose \(\mathord{\equiv}\) is an equivalence relation on a nonempty set \(A\text{.}\)

1. For every \(a \in A\text{,}\) we have \(a \in [a]\text{.}\)
2. For \(a,a_1,a_2 \in A\) with \(a_1,a_2 \in [a]\text{,}\) we have \(a_1 \equiv a_2\text{.}\)
3. For each pair \(a_1,a_2 \in A\text{,}\) we have \(a_1 \equiv a_2\) if and only if \([a_1] = [a_2]\text{.}\)
4. For each pair \(a_1,a_2 \in A\text{,}\) we have \(a_1 \not\equiv a_2\) if and only if \([a_1] \cap [a_2] = \emptyset\text{.}\)

Proof

Proof of Statement 1.
This is just the reflexive property, \(a \equiv a\text{.}\)

Proof of Statement 2.
If \(a_1,a_2 \in [a]\text{,}\) then by definition we have both \(a_1 \equiv a\) and \(a_2 \equiv a\text{.}\) Applying symmetry to the latter equivalence, we may write \(a_1 \equiv a \equiv a_2\text{,}\) to which we may apply transitivity to obtain \(a_1 \equiv a_2\text{,}\) as desired.

Proof of Statement 3.
(⇒)
Suppose \(a_1 \equiv a_2\text{.}\) To verify \([a_1] = [a_2]\text{,}\) we follow the Test for Set Equality. First, assume \(x\) is an arbitrary element in \([a_1]\text{.}\) Then \(x \equiv a_1 \equiv a_2\text{,}\) so \(x \equiv a_2\) by the transitive property. Therefore, \(x \in [a_2]\text{,}\) as required. This shows that \([a_1] \subseteq [a_2]\text{;}\) the argument to show \([a_2] \subseteq [a_1]\) is almost exactly the same, just using the symmetric property to first obtain \(a_2 \equiv a_1\text{.}\)

(⇐)
By Statement 1 of this proposition, we have \(a_1 \in [a_1]\text{.}\) If we assume \([a_1] = [a_2]\text{,}\) then we also have \(a_1 \in [a_2]\text{,}\) which means that \(a_1 \equiv a_2\text{,}\) as required.

Proof of Statement 4.
Let us prove the equivalent “double contrapositive” biconditional \(a_1 \equiv a_2 \Leftrightarrow [a_1] \cap [a_2] \ne \emptyset\text{.}\) (See Worked Example 2.1.2.)

(⇒)
Suppose \(a_1 \equiv a_2\text{.}\) Then \([a_1] = [a_2]\) by Statement 3, so

\begin{equation*} [a_1] \cap [a_2] = [a_1] \cap [a_1] = [a_1] \text{.} \end{equation*}
But \([a_1]\) is nonempty by Statement 1.

(⇐)
Suppose \([a_1] \cap [a_2] \ne \emptyset\text{.}\) Then there exists some element \(x \in A\) that is in both \([a_1]\) and \([a_2]\text{,}\) so that both \(x \equiv a_1\) and \(x \equiv a_2\text{.}\) By the symmetric property, we have \(a_1 \equiv x\text{,}\) and combining this with \(x \equiv a_2\) in the transitive property gives \(a_1 \equiv a_2\text{.}\)

Statement 3 of Proposition \(\PageIndex{1}\) tells us that any member of an equivalence class may be used to define the class.

Definition: equivalence class representative

an element \(a \in A\) used to define the equivalence class

\begin{equation*} [a] = \{x\in A \vert x \equiv a \} \end{equation*}

Definition: complete set of equivalence class representatives

a subset \(C \subseteq A\) so that for each \(x \in A\) there exists exactly one \(a \in C\) so that \(x \in [a]\)

Remember that elements that are equivalent to one another relative to some equivalence relation are viewed to be “essentially the same” from the point of view of the property used to define the equivalence relation. So different but equivalent elements become interchangeable (see Section 18.1). When we have a complete set of representatives for the equivalence classes, we are deciding to always interchange an element for the chosen representative of the class containing that element.

Example \(\PageIndex{3}\): A complete set of equivalence class representatives for natural numbers modulo \(5\).

Continuing Example \(\PageIndex{2}\), we could represent the class of numbers that have remainder \(3\) by the number \(8\text{:}\)

\begin{equation*} [8] = \{ 3, 8, 13, 18, \ldots \} \text{.} \end{equation*}
But it seems more “natural” to represent this class by the number \(3\text{:}\)

\begin{equation*} [3] = \{ 3, 8, 13, 18, \ldots \} \text{.} \end{equation*}
Notice that each of the numbers \(0,1,2,3,4\) has a different remainder when divided by \(5\text{,}\) so no two of them are equivalent. That also means that each is in a different class (Statement 4 of Proposition \(\PageIndex{1}\)). But when we go past \(4\text{,}\) the remainders when divided by \(5\) start repeating: each of the numbers in the list \(5,6,7,8,9\) has the same remainder as the number in the corresponding position in the list \(0,1,2,3,4\text{.}\) And then the remainders repeat again when we go past \(9\text{.}\) And so on. So it seems “natural” to use \(0,1,2,3,4\) as a complete set of representatives of the equivalence classes for \(\mathbb{N}\) modulo \(5\text{:}\)

\begin{align*} [0] & = \{ 0, 5, 10, 15, \ldots \}, \\ [1] & = \{ 1, 6, 11, 16, \ldots \}, \\ [2] & = \{ 2, 7, 12, 17, \ldots \}, \\ [3] & = \{ 3, 8, 13, 18, \ldots \}, \\ [4] & = \{ 4, 9, 14, 19, \ldots \}. \end{align*}

The definition of complete set of equivalence class representatives implicitly assumes that the equivalence classes “fill up” the whole set \(A\text{.}\) But that is always precisely the case.

Definition: Partition

a collection of subsets of a set \(A\) that are pairwise disjoint and whose union is \(A\)

Definition: Partition Cell

one of the subsets that make up a partition of a set

Figure \(\PageIndex{1}\): A diagram illustrating a partition of a set, so that \(A = A_1 \sqcup A_2 \sqcup A_3 \sqcup \ldots \sqcup A_n\text{.}\)

Remark \(\PageIndex{1}\)

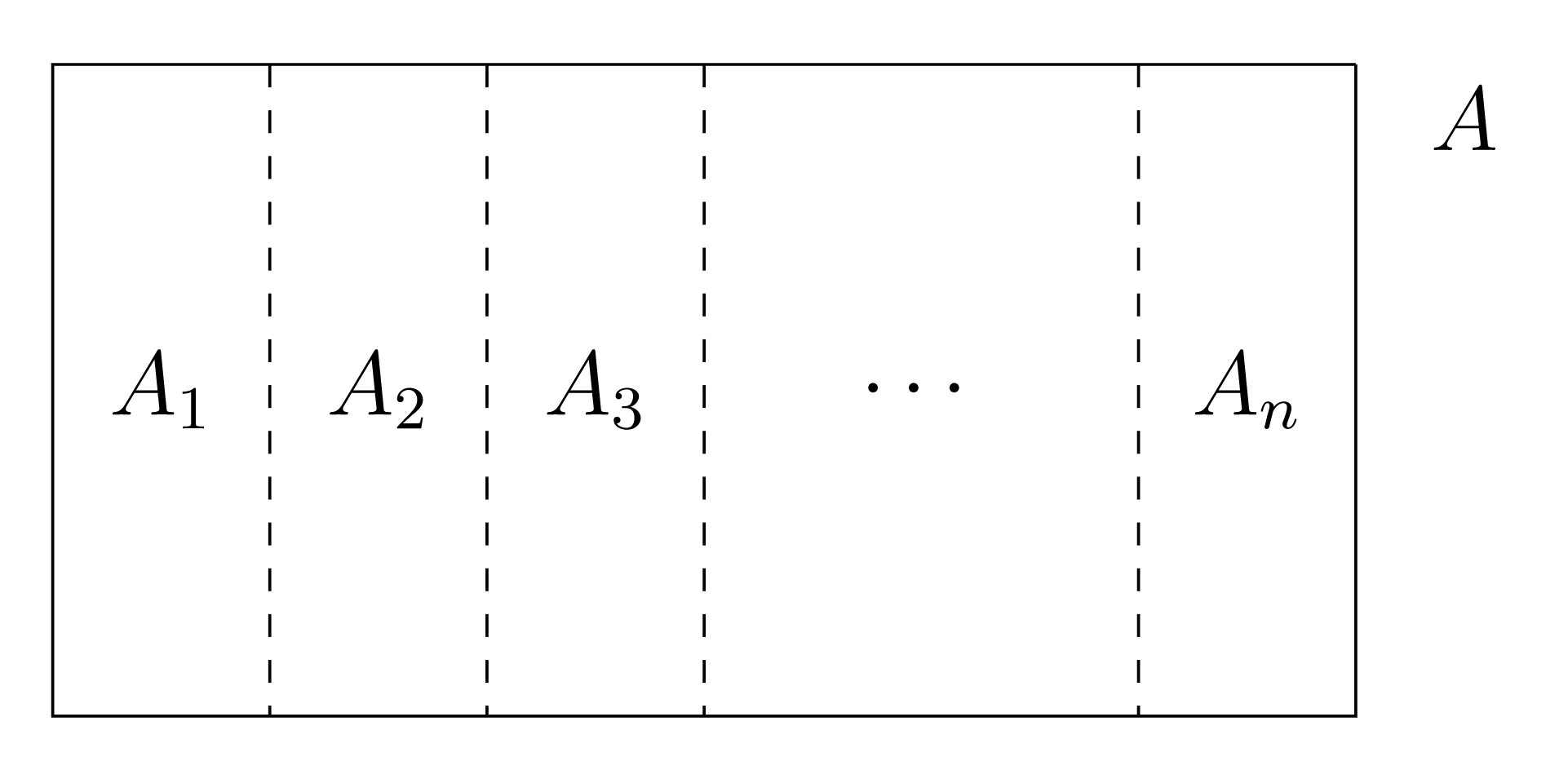
In essence, partition is just a synonym for disjoint union. So a collection of subsets form a partition when each element of the set is in exactly one partition cell.

Note \(\PageIndex{1}\)

It is not necessary for a partition of a set to be made up of a finite (or even countable) number of cells; see the examples below.

Theorem \(\PageIndex{1}\): Equivalence classes form a partition.

If \(\mathord{\equiv}\) is an equivalence relation on a set \(A\text{,}\) then the equivalence classes with respect to \(\mathord{\equiv}\) are a partition of \(A\text{.}\)

Proof Idea

This theorem claims that every element of \(A\) is in exactly one equivalence class. But this follows from the statements of Proposition \(\PageIndex{1}\).

Example \(\PageIndex{4}\): Equivalence classes modulo \(n\).

Generalizing Example \(\PageIndex{3}\), each of the numbers \(0,1,2,3,\ldots,n-1\) is its own remainder when divided by \(n\text{.}\) And then the pattern of remainders repeats, starting over at remainder \(0\text{,}\) when we continue on to the numbers \(n,n+1,\ldots\text{.}\) So \(0,1,2,3,\dots,n-1\) is a complete set of equivalence class representatives, and the classes modulo \(n\) partition \(\mathbb{N}\) into the disjoint subsets

\begin{align*} [0] & = \{ \, 0, \, n, 2n, \, 3n, \, \ldots \, \}, \\ [1] & = \{ \, 1, \, n+1, 2n+1, \, 3n+1, \, \ldots \, \}, \\ [2] & = \{ \, 2, \, n+2, 2n+2, \, 3n+2, \, \ldots \, \}, \\ \phantom{[0]} & \vdots \\ [n-1] & = \{ \, n-1, \, 2n-1, 3n-1, \, 4n-1, \, \ldots \, \}. \end{align*}

Example \(\PageIndex{5}\)

Let \(\scr{L}\) be the set of all lines in the plane, and consider \(\ell_1 \equiv \ell_2\) if \(\ell_1, \ell_2\) are parallel. Then \(\mathord{\equiv}\) partitions \(\scr{L}\) into sets of parallel lines.

Example \(\PageIndex{6}\)

Recall that for alphabet \(\Sigma\text{,}\) \(\Sigma^\ast_n\) is the subset of \(\Sigma^\ast\) consisting of all words whose length is exactly \(n\text{.}\) Then

\begin{equation*} \Sigma^\ast_0, \Sigma^\ast_1, \Sigma^\ast_2, \ldots \end{equation*}
is a partition of \(\Sigma^\ast\text{.}\) (See Exercise 9.9.9.)

Recall that a relation on \(\Sigma^\ast\) can be defined as a subset of \(\Sigma^\ast \times \Sigma^\ast\text{.}\) So consider the relation \(R\) on \(\Sigma^\ast\) defined by

\begin{equation*} R \;\; =\;\; (\Sigma^\ast_0 \times \Sigma^\ast_0) \;\; \sqcup \;\; (\Sigma^\ast_1 \times \Sigma^\ast_1) \;\; \sqcup \;\; (\Sigma^\ast_2 \times \Sigma^\ast_2) \;\; \sqcup \;\; \ldots \end{equation*}
Then \(R\) is the equivalence relation on \(\Sigma^\ast\) where \(w \mathrel{R} y\) if \(\vert w \vert = \vert y \vert\text{,}\) and its equivalence classes are precisely the sets \(\Sigma^\ast_n\text{,}\) \(n\ge 0\text{.}\)

Theorem \(\PageIndex{2}\): Partitions arise from equivalence relations.

Given a partition of a set \(A\text{,}\) there exists an equivalence relation \(\mathord{\equiv}\) on \(A\) whose equivalence classes are precisely the cells of the partition.

Proof Idea.

Given a partition of \(A\text{,}\) for each \(a \in A\) there exists exactly one partition cell containing \(a\text{.}\) So define \(a_1 \equiv a_2\) to mean “elements \(a_1,a_2\) are contained in the same partition cell of \(A\text{.}\)”

Remark \(\PageIndex{2}\)

Theorem \(\PageIndex{1}\) and Theorem \(\PageIndex{2}\) combine to provide, for each set \(A\text{,}\) a bijective correspondence

\begin{equation*} \{ \text{equivalence relations on } A \} \;\; \longleftrightarrow \;\; \{ \text{partitions of } A \}. \end{equation*}

Example \(\PageIndex{7}\): Determining an equivalence relation from a partition.

Determine an explicit equivalence relation \(\mathord{\equiv}\) on \(\mathbb{Z}\) for which the equivalence classes give the following partition.

\begin{equation*} \mathbb{Z} \;\; = \;\; \ldots \;\; \sqcup \;\; \{ -3, -2, -1 \} \;\; \sqcup \;\; \{ 0, 1, 2 \} \;\; \sqcup \;\; \{ 3, 4, 5 \} \;\; \sqcup \;\; \ldots \end{equation*}

Solution

Notice that each cell in the partition contains a multiple of \(3\) along with the next two consecutive integers. So one way to explicitly define the corresponding equivalence relation is: for \(a,b \in \mathbb{Z}\text{,}\) define \(a \equiv b\) to be true if there exists \(n \in \mathbb{Z}\) such that \(3 n \le a,b \le 3 n + 2\text{.}\) (Note: Details showing that this is an equivalence relation are omitted.)

Definition: Quotient (of a set \(A\) relative to an equivalence relation \(\mathord{\equiv}\))

the subset of \(\mathscr{P}(A)\) whose elements are the equivalence classes of \(\mathord{\equiv}\)

Definition: \(A / \mathord{\equiv} \)

the quotient of \(A\) relative to equivalence relation \(\mathord{\equiv}\text{,}\) so that

\begin{equation*} (A / \mathord{\equiv}) = \{[a] \vert a \in A\} \end{equation*}

Example \(\PageIndex{8}\): A quotient described by class representatives.

Consider the partition of \(\mathbb{Z}\) from Worked Example \(\PageIndex{7}\), and the corresponding equivalence relation \(\mathrel{\equiv}\text{.}\) To describe \(\mathbb{Z} / \equiv\text{,}\) we just need to pick a representative of each class. The most obvious way in this case is

\begin{equation*} (\mathbb{Z} / \mathord{\equiv}) = \{ \ldots, [-3], [0], [3], [6], \ldots \} \text{.} \end{equation*}

Example \(\PageIndex{9}\): Determining a quotient.

Let \(\mathord{\equiv}\) represent the equivalence relation on \(\mathbb{Z}\) defined by

\(0 \equiv 0\text{,}\) and

for non-zero \(m,n \in \mathbb{Z}\text{,}\)

\begin{align*} m & \equiv n & & \text{if} & \dfrac{m}{\vert m \vert} & = \dfrac{n}{\vert n \vert} \text{.} \end{align*}

Determine the corresponding partition and quotient of \(\mathbb{Z}\text{.}\)

Solution

First notice that \(0\) will be in an equivalence class all by itself. Next, consider the values that \(m/\vert m \vert\) can possibly take.

If \(m \gt 0\text{,}\) then \(\vert m \vert = m\) so \(m/\vert m \vert = 1\text{.}\)

If \(m \lt 0\text{,}\) then \(\vert m \vert = - m\) so \(m/\vert m \vert = -1\text{.}\)

So this equivalence relation is just a fancy way of saying that \(m,n\) have the same sign. Therefore, all positive numbers will be in the same equivalence class, and all negative numbers will be in the same equivalence class. It now makes sense that \(0\) is in a class by itself, since \(0\) is neither positive nor negative. The partition of \(\mathbb{Z}\) corresponding to \(\mathord{\equiv}\) is then

\begin{equation*} \mathbb{Z} \;\; = \;\; \{ \ldots, -3, -2, -1 \} \;\; \sqcup \;\; \{ 0 \} \;\; \sqcup \;\; \{ 1, 2, 3, \ldots \}\text{.} \end{equation*}
To describe \(\mathbb{Z} / \mathord{\equiv}\text{,}\) we just need to pick a representative of each equivalence class. One possibility is

\begin{equation*} \mathbb{Z} = [-1] \sqcup [0] \sqcup [1] \text{,} \end{equation*}
so that

\begin{equation*} (\mathbb{Z} / \mathord{\equiv}) = \{ [-1], [0], [1] \} \text{.} \end{equation*}

Definition: natural projection (on a set \(A\) relative to an equivalence relation \(\mathord{\equiv}\))

the function \(A \to (A / \mathord{\equiv})\) defined by \(a \mapsto [a]\)

Note \(\PageIndex{2}\)

The natural projection \(A \to (A / \mathord{\equiv})\) is always surjective, but it is almost never injective.

Example \(\PageIndex{10}\): Natural projection modulo-\(5\).

Recall that \(\mathord{\equiv}_5\) represents the modulo-\(5\) equivalence relation on \(\mathbb{N}\text{.}\) In Example \(\PageIndex{3}\) we determined that there are five equivalence classes, represented by elements \(0,1,2,3,4\text{,}\) so that

\begin{equation*} (\mathbb{N} / \mathord{\equiv}_5) = \{[0],[1],[2],[3],[4]\} \text{.} \end{equation*}
Below are some examples of images of elements under the natural projection.

\begin{align*} 2 & \mapsto [2] & 7 & \mapsto [2] & 104 & \mapsto [4] & 76 & \mapsto [1] & 2045 & \mapsto [0]\text{.} \end{align*}