19.8: Exercises
- Page ID
- 93879
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recognizing a partial order from its graph.
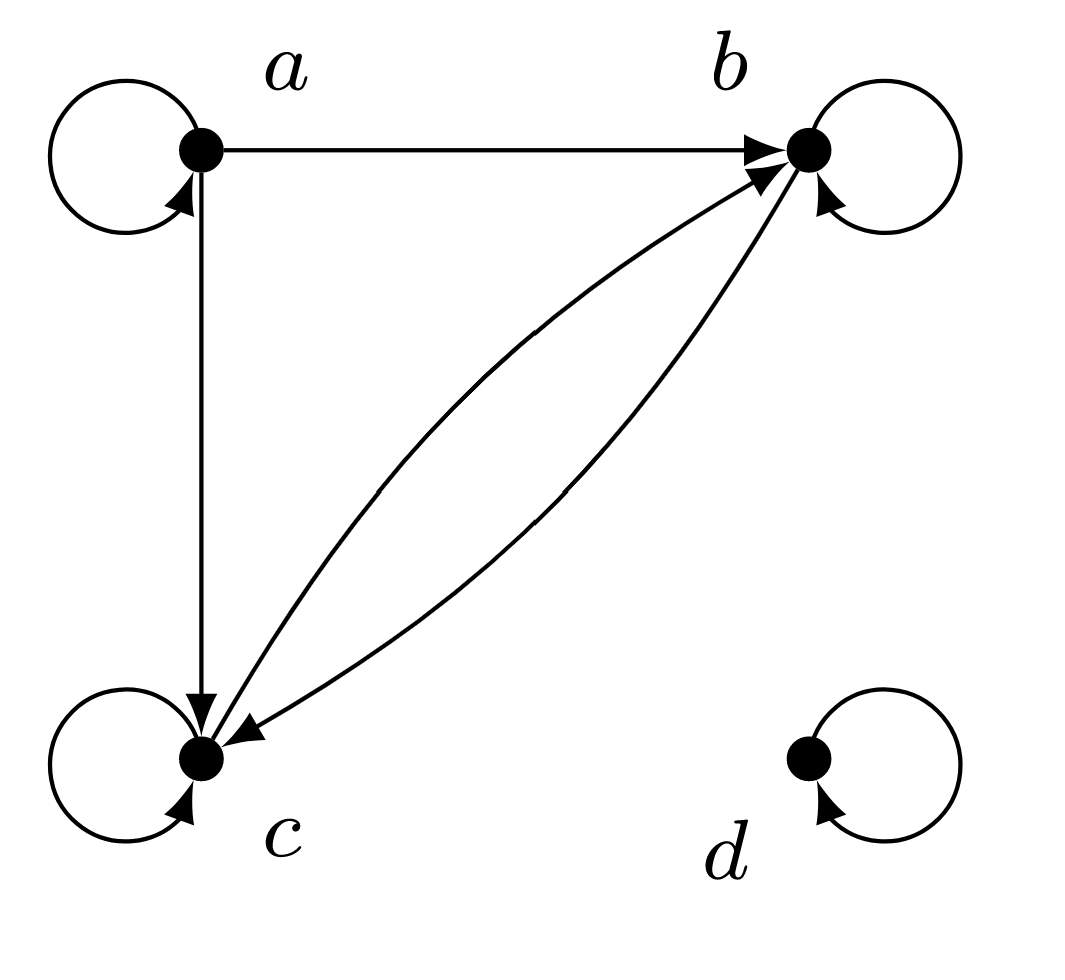
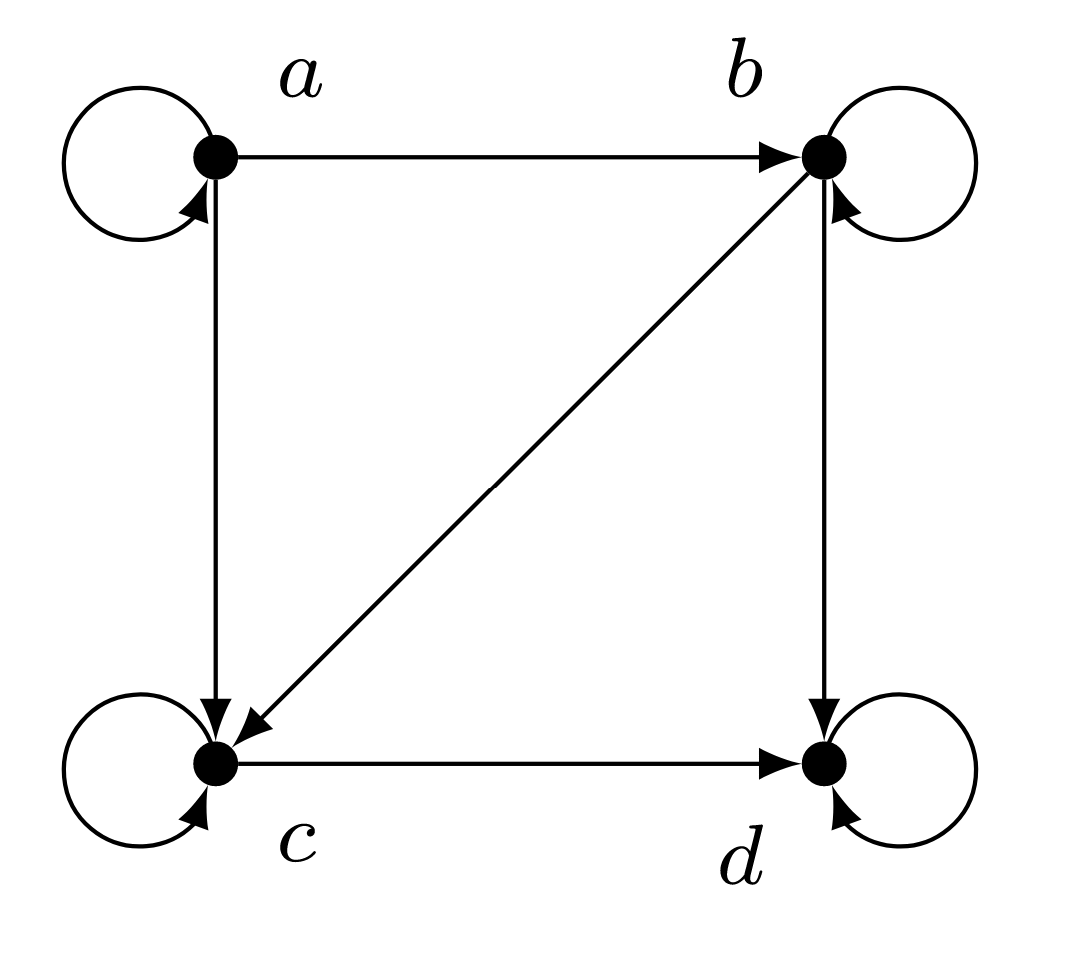
In each of Exercises 1–2, you are given a directed graph for a relation on the set \(A = \{a,b,c,d\}\text{.}\) Determine whether the relation is a partial order. Justify your answers.
Exercise \(\PageIndex{1}\)
Exercise \(\PageIndex{2}\)
Testing partial orders.
In each of Exercises 3–6, you are given a set \(A\) and a relation \(R\) on \(A\text{.}\) Determine whether the relation is a partial order. Justify your answers.
Exercise \(\PageIndex{3}\)
\(A\) is the set of all Augustana students; \(a \mathrel{R} b\) means that student \(a\) has a higher GPA than student \(b\text{.}\)
Exercise \(\PageIndex{4}\)
\(A\) is the power set of some finite set; \(S \mathrel{R} T\) means \(\vert S \vert \le \vert T \vert \text{.}\)
Exercise \(\PageIndex{5}\)
\(A\) is the set of words on some alphabet; \(w \mathrel{R} w'\) means \(\vert w \vert \le \vert w' \vert \text{,}\) where \(\vert w \vert\) means the length of word \(w\text{.}\)
Exercise \(\PageIndex{6}\)
\(A = \mathbb{R} \times \mathbb{R}\text{;}\) \((x_1, y_1) \mathrel{R} (x_2,y_2)\) means \(x_1 \le x_2\) and \(y_1 \le y_2\text{.}\)
Drawing Hasse diagrams.
In each of Exercises 7–8, you are given a finite, partially ordered set \(A\text{.}\) Draw the Hasse diagram.
Exercise \(\PageIndex{7}\)
\(A = \mathscr{P}(\{1,2,3,4\})\) under the subset relation.
Exercise \(\PageIndex{8}\)
\(A = \Sigma^\ast_4\text{,}\) the set of words of length \(4\) in the alphabet \(\Sigma = \{0,1\}\text{,}\) under dictionary order.
Exercise \(\PageIndex{9}\)
Draw all possible valid Hasse diagrams for each of the sets \(A = \{a,b\}\) and \(B = \{a,b,c\}\text{.}\) (Thus, you will have determined all possible partial orders on those sets.)
Exercise \(\PageIndex{10}\)
Consider the “divides” relation \(\mathord{\mid}\) on \(\mathbb{N}_{>0}\text{.}\) Provide an example of a set \(A \subseteq \mathbb{N}_{>0}\)
- that is finite, and on which \(\mathord{\mid}\) is a total order.
- that is infinite, and on which \(\mathord{\mid}\) is a total order.
- on which \(\mathord{\mid}\) is a partial order but not a total order.
Exercise \(\PageIndex{11}\)
Let \(A = \{0,1,2\}\text{,}\) and consider the partial order \(\mathord{\subseteq}\) on the power set \(\mathscr{P}(A)\text{.}\) List all pairs of incomparable elements in \(\mathscr{P}(A)\text{.}\)
Determining maximal/maximum/minimal/minimum elements.
In each of Exercises 12–16, you are given a partially ordered set \(A\text{.}\) Determine any and all maximal, maximum, minimal, and minimum elements.
Exercise \(\PageIndex{12}\)
\(A = \mathbb{N}_{>0}\) under the usual \(\mathord{\le}\text{.}\)
Exercise \(\PageIndex{13}\)
\(A = \mathbb{Q}_{>0}\) under the usual \(\mathord{\le}\text{.}\)
Exercise \(\PageIndex{14}\)
\(A = \mathbb{N} \setminus \{0,1\}\) under the “divides” relation \(\mathord{\mid}\text{.}\)
Exercise \(\PageIndex{15}\)
\(A = \{2,5,11,13,22,65,110,143,496\}\) under the “divides” relation \(\mathord{\mid}\text{.}\)
Exercise \(\PageIndex{16}\)
\(A\) is the set of the first ten prime numbers under the “divides” relation \(\mathord{\mid}\text{.}\)
Exercise \(\PageIndex{17}\)
Suppose \(\mathord{\preceq}\) is a partial order on the set \(A = \{0,1,2\}\) such that \(1\) is a maximal element. What are the possibilities for the Hasse diagram of \(\mathord{\preceq}\text{?}\)
Topological sorting.
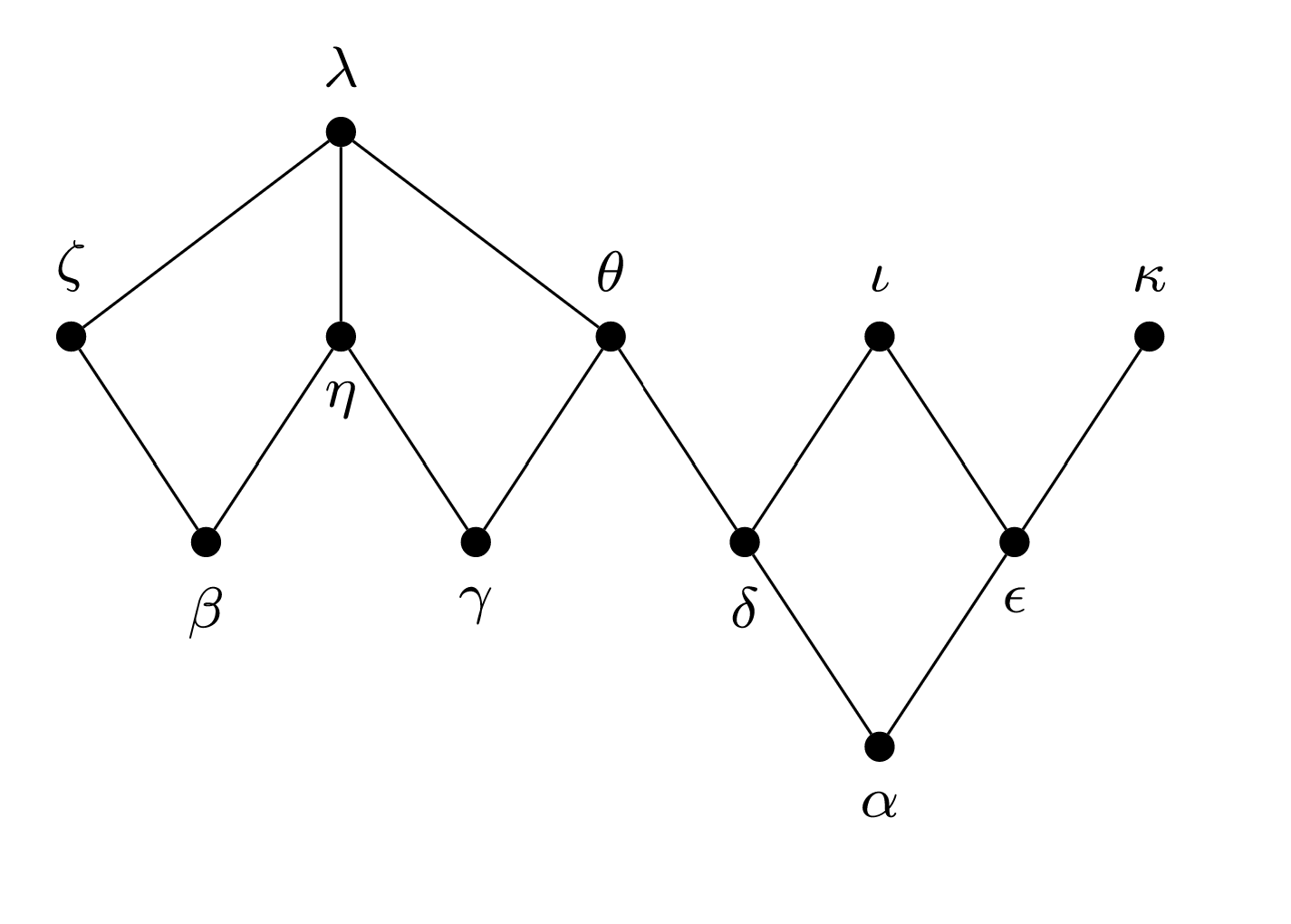
In each of Exercises 18–19, you are given the Hasse diagram for a partially ordered set \(A\text{.}\) Use the Topological sorting algorithm to determine a compatible total order on \(A\text{.}\)
Exercise \(\PageIndex{18}\)
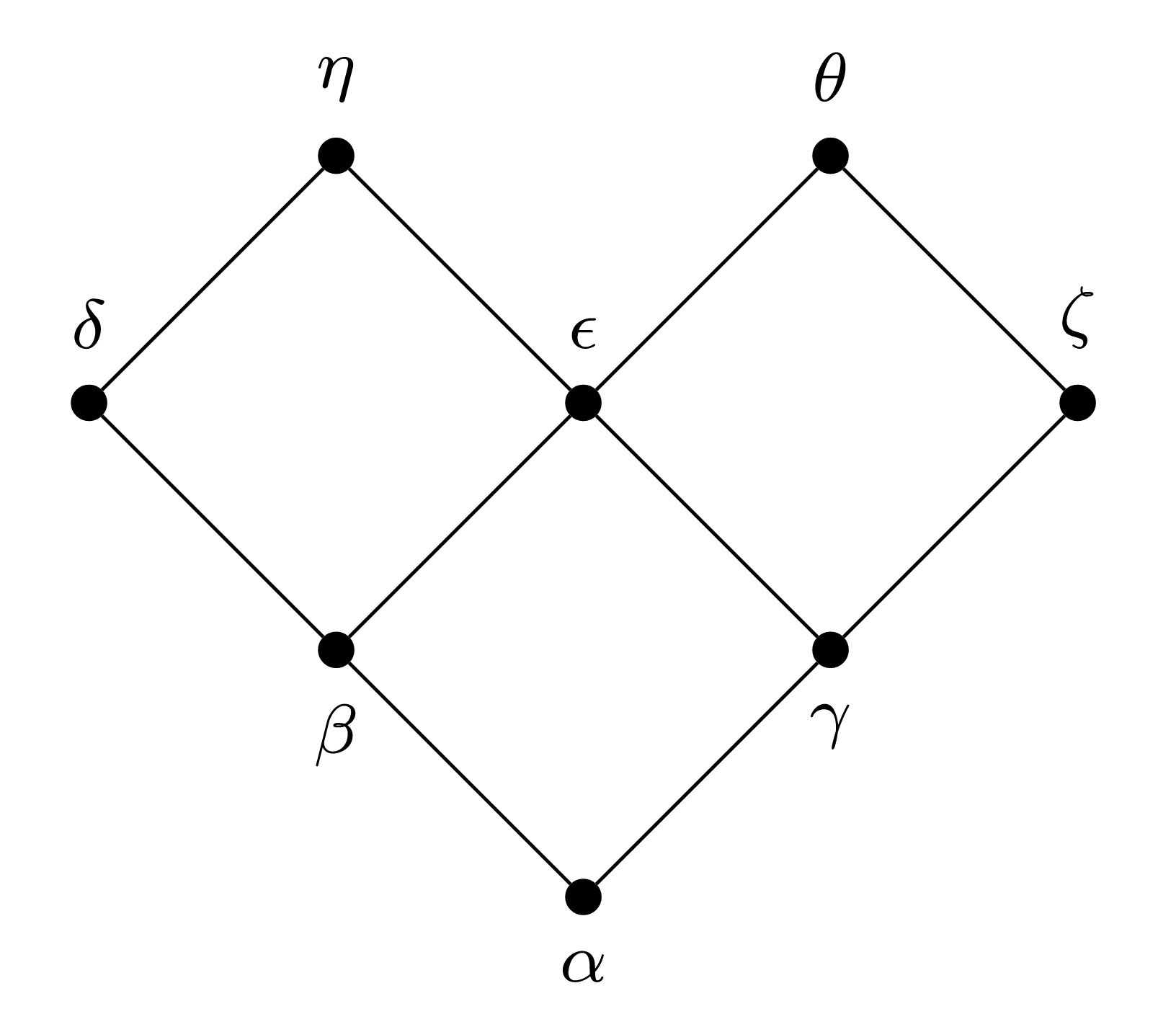
Exercise \(\PageIndex{19}\)
