1.3: Proof by Induction

A brief exploration

Suppose you were playing around with the smallest positive perfect squares (a list is found in Appendix B), and you decided to look for patterns in their sums. You might compute

\[\begin{aligned} 1 &= 1;\\ 5 &= 1+4;\\ 14 &= 1+4+9;\\ 30 &= 1+4+9+16;\\ 55 &= 1+4+9+16+25;\\ 91 &= 1+4+9+16+25+36;\\ 140 &= 1+4+9+16+25+36+49;\\ 204 &= 1+4+9+16+25+36+49+64.\end{aligned}\]

and wonder what patterns exist in this "sums of squares" sequence \[1,5,14,30,55,91,140,204,\dots.\nonumber \]

Plotting these numbers as points in the coordinate plane, i.e., plotting \((1,1), (2,5), (3,14), (4,30)\), and so on yields the following picture:

Figure \(\PageIndex{1}\)

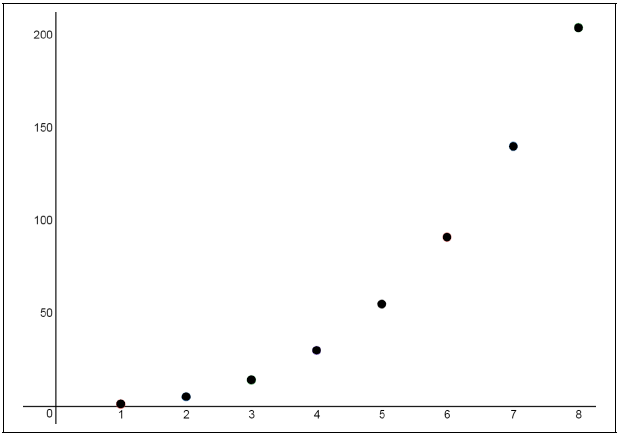
From a first glance at the picture, it looks like the the points certainly fit a smooth curve—perhaps a parabola or other polynomial curve, or perhaps the graph of an exponential function. One thing we don't know is the equation of this curve.

Looking at the sums-of-squares numbers \(1,5,14,30,55,91,140,204,\dots\) again, and heading in perhaps a different direction, we might look at their prime factorizations:\(^{1}\)

\[\begin{aligned} 1 &\\ 5 &= 5;\\ 14 &= 2\cdot 7;\\ 30 &= 2\cdot 3 \cdot 5;\end{aligned}\]

\[\begin{aligned} 55 &= 5 \cdot 11;\\ 91 &= 7 \cdot 13;\\ 140 &= 2^2\cdot 5\cdot 7;\\ 204 &= 2^2 \cdot 3 \cdot 17.\end{aligned}\]

One thing that stands out about the factorizations are the numbers 5, 7, 11, 13, and 17. Other than in the factorizations of 30 and 140 (where we don't see 9 or 15), it looks as though the last number in each successive factorization is just the next odd number. In fact, if we forgot about prime factorizations and rewrote the factorizations of 1, 30, and 140 above, we would see the pattern even more clearly:

\[\begin{aligned} 1 &= \frac{1}{3}\cdot 3;\\ 5 &= 5;\\ 14 &= 2\cdot 7;\\ 30 &= \frac{1}{3} \cdot 2 \cdot 5 \cdot 9 ;\end{aligned}\]

\[\begin{aligned} 55 &= 5 \cdot 11;\\ 91 &= 7 \cdot 13;\\ 140 &= \frac{1}{3} \cdot 2^2\cdot 7\cdot 15;\\ 204 &= 2^2 \cdot 3 \cdot 17.\end{aligned}\]

Note that in order to make 3, 9, and 15 appear in the expected places, we had to introduce the fraction \(\frac{1}{3}\) in front of a few of the lines.

But now can we explain the patterns in the other factors appearing before the final odd factors? Can we explain why some lines need the fraction in the front while the others don't seem to? Through a little clever manipulation and perhaps some luck, we might happen on the following ways of writing our sums-of-squares numbers:

\[\begin{aligned} 1 &= \frac{1}{6} \cdot 1 \cdot 2 \cdot 3;\\ 5 &= \frac{1}{6} \cdot 2 \cdot 3 \cdot 5;\\ 14 &= \frac{1}{6} \cdot 3 \cdot 4 \cdot 7;\\ 30 &= \frac{1}{6} \cdot 4 \cdot 5 \cdot 9 ;\end{aligned}\]

\[\begin{aligned} 55 &= \frac{1}{6} \cdot 5 \cdot 6 \cdot 11;\\ 91 &= \frac{1}{6} \cdot 6 \cdot 7 \cdot 13;\\ 140 &= \frac{1}{6} \cdot 7 \cdot 8 \cdot 15;\\ 204 &= \frac{1}{6} \cdot 8 \cdot 9 \cdot 17.\end{aligned}\]

There's definitely a pattern here. In fact, looking at \[\begin{aligned} 1^2 &= \frac{1}{6} \cdot 1 \cdot 2 \cdot 3,\\ 1^2+2^2 &= \frac{1}{6} \cdot 2 \cdot 3 \cdot 5,\\ 1^2+2^2+3^2 &= \frac{1}{6} \cdot 3 \cdot 4 \cdot 7,\end{aligned}\] and so on, we might guess that the following is true:

If \(n\) is any positive integer, then \[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber \]

Plotting \(y=\frac{1}{6}x(x+1)(2x+1)\) on the coordinate plane, we get a curve that passes perfectly through the points on our graph from before, and as we expected, our conjectured formula for the numbers is a polynomial—it's a cubic function.

At this point we believe we've discovered a formula for the sum of the first \(n\) positive square numbers. However, other than by just appealing to our observations (which is rarely good enough for a mathematician), how would we prove that our formula is correct?

Proofs by mathematical induction

We now discuss a powerful tool for answering questions like the one above and for proving statements about integers. This tool will reappear at various places throughout this text. It is the Principle of Mathematical Induction introduced in the previous chapter, which we will refer to by PMI or simply induction. Here it is again, slightly restated:\(^{2}\)

The Principle of Mathematical Induction

If a statement about integers satisifes both

1. the statement is true for the number \(n_0\), and
2. whenever the statement is true for each of the numbers \[n_0,\: n_0+1,\ldots ,k,\nonumber\] the statement is true for \(k + 1\) as well,

then the statement is true for integer greater than or equal to \(n_0\).

There is a lot to digest in this principle. We illustrate it with a few examples, pointing out some key features of induction along the way.

We begin with our conjectured statement about the sums of squares. We call the statement we want to prove a proposition. It might also be called a theorem, lemma or corollary depending on the situation. Here again is our statement.

Proposition \(\PageIndex{1}\)

If \(n\) is any positive integer, then \[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber \]

Proof

As we think about a proof, this statement seems like a good candidate for a proof using PMI. Why is this?

Key Idea

PMI is a proof technique designed specifically for statements of the form \[P(n)\text{ for all integers }n\geq n_0.\nonumber\] where \(P(n)\) is a statement depending on an integer \(n\), and \(n_0\) is a specific integer.

Now the proposition above is written as an "if/then" statement, but it can be rephrased as \[\text{``}1^2+2^2+\cdots +n^2=\frac{1}{6}n(n+1)(2n+1)\text{ for all integers }n\geq 1\text{''.}\nonumber\]

This makes it a good candidate for PMI, and, using the notation of the key idea above, it also tells us two things:

• \(P(n)\) is the statement "\(\displaystyle 1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1)\)";
• \(n_0 = 1\).

Before proceeding, a few things are worth noting. First, the notation \(P(n)\) is used to suggest that values of \(n\) can be substituted into the \(P(n)\). If \(n=1\) then our \(P(n)\) becomes \(P(1)\), i.e., the statement \(1^2=\frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1)\), and if \(n=2\) then \(P(n)\) becomes \(P(2)\), which is the statement \(1^2+2^2 = \frac{1}{6}\cdot 2(2+1)(2\cdot 2 + 1)\).

Next, it is important to note that \(P(n)\) is the full equation, not simply \(1^2+2^2+\cdots+n^2\) or \(n^2\) or \(\frac{1}{6}n(n+1)(2n+1)\); instead of an expression, it is a statement. This will virtually always be the case: if you've correctly identified what \(P(n)\) should be, then \(P(n)\) will be a complete mathematical sentence, such as an equation or inequality, thought it may sometimes be a more complicated English sentence,\(^{3}\) perhaps spanning multiple lines.

Carrying on towards a proof of our proposition, now that we have recognized that the statement has a suitable form for using PMI, and we have identified \(P(n)\) and \(n_0\), we are ready to start assembling a proof. A proof by induction shows that \(P(n)\) satisfies both the conditions (a) and (b) in the Principle:

Simplified outline of a proof using PMI:

PMI(a) Explain why \(P(n_0)\) is true.\(^{4}\)
PMI(b) Carefully justify the following: If \(P(n)\) is known to be true for all values of \(n\) such that \(n_0\leq n\leq k\) and \(k\) is some integer, then these statements imply that \(P(k +1)\) is true. Said another way, what we need to prove is that \[\text{if }P(n_0);\: P(n_0 + 1);\: P(n_0 + 2);\ldots P(k)\text{ are all true, then }P(k + 1)\text{ must be true, too.}\nonumber\]

What does this outline look like for our proposition?

Step PMI(a) requires a demonstration that \(P(n_0)\) is true. For us this means that we must explain why \(P(1)\) is true, i.e., why \[1^2 = \frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1).\nonumber \] Since both sides of the equation equal 1, this can immediately be seen to be true; we just need to state it in the proof, and PMI(a) will be complete.

Now, since PMI(b) is an if/then statement, to prove it we begin by assuming or supposing, just for the sake of argument, that \[P(n) \text{ is true for } 1 \le n \le k.\nonumber \] That is, we assume \[\label{ind_hyp} 1^2 + 2^2 + \cdots + n^2 = \frac{1}{6}n(n+1)(2n+1)\mbox { for } 1 \le n \le k.\]

Another way to say this is that we suppose that \[\begin{gathered} \nonumber 1^2 = \frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1),\\ \nonumber 1^2+2^2 = \frac{1}{6}\cdot 2(2+1)(2\cdot 2 + 1),\\ \nonumber \vdots\\ \nonumber 1^2+2^2+\cdots+k^2 = \frac{1}{6}\cdot k(k+1)(2k + 1)\end{gathered}\] are all true statements, and we would like to see what these would imply.

The assumption \(\eqref{ind_hyp}\) is called the induction hypothesis; it is the "if" part of the "if/then" we are proving in PMI(b). Remember, to prove this implication, we suppose that the statement \(P(n)\) is known to be true for every choice of \(n\) between \(n_0\) and \(k\), and we then show how to use these facts to prove that \(P(n)\) holds when \(n=k+1\). Proving that \(P(k+1)\) is true is sometimes called the induction step.

Here is one way to carry out the inductive step in our example. We take the equation \[1^2+2^2+\cdots+k^2=\frac{1}{6}k(k+1)(2k+1)\nonumber \] (which is \(P(k)\), one of the equations we agreed to suppose was true in the induction hypothesis) and add \((k+1)^2\) to both sides to get \[ \label{indeq1} 1^2+2^2+\cdots+k^2 + (k+1)^2=\frac{1}{6}k(k+1)(2k+1) + (k+1)^2. \] Note that we are trying to prove \(P(k+1)\), so we would like to show that \[1^2+2^2+\cdots+ (k+1)^2=\frac{1}{6}(k+1)(k+1+1)(2(k+1)+1);\nonumber \] we are not quite there yet. The last two equations above do agree on the left-hand side, which is good, but the right-hand sides are not yet the same; how will we justify \(P(k+1)\)?

Here, all that is needed is simple algebraic manipulation. Starting from equation \(\eqref{indeq1}\), we can write \[\begin{aligned} 1^2+2^2+\cdots+k^2 + (k+1)^2 &=\frac{1}{6}k(k+1)(2k+1) + (k+1)^2\\ &= \frac{1}{6}k(k+1)(2k+1) + \frac{1}{6} \cdot 6(k+1)^2\\ &= \frac{1}{6}(k+1)\left[k(2k+1)+6(k+1)\right]\\ &= \frac{1}{6}(k+1)\left(2k^2+7k+6\right)\\ &= \frac{1}{6}(k+1)(k+2)(2k+3)\\ &= \frac{1}{6}(k+1)(k+1+1)(2(k+1)+1),\end{aligned}\] which shows that \(P(k+1)\) can be proved if we know that \(P(1),\cdots,P(k)\) are true. Thus we have established PMI(b), and PMI tells us that since PMI(a) and PMI(b) hold, the statement \(P(n)\) is true for \(n\geq 1\). We have finished!

Summarizing the discussion above, we now give a less pedagogical, more streamlined proof, which is more in line with the kinds of proofs you should strive for.

Proposition \(\PageIndex{2}\)

If \(n\) is any positive integer, then \[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber\]

Proof

We prove the proposition by induction on the variable \(n\).

When \(n=1\) we find \[1^2 = 1 = \frac{1}{6}\cdot 1(1+1)(2\cdot 1 + 1),\nonumber \] so the claimed equation is true when \(n=1\).

Assume that \[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1) \quad \text{for }1 \leq n \leq k \quad \text{(the induction hypothesis)}.\nonumber \] Taking \(n = k\) we have \[1^2+2^2+\cdots+k^2 = \frac{1}{6}k(k+1)(2k+1).\nonumber \] Then \[\begin{aligned} 1^2+2^2+\cdots+(k+1)^2 &= \left[1^2+2^2+\cdots+k^2\right] + (k+1)^2 \\ &=\frac{1}{6}k(k+1)(2k+1) + (k+1)^2 \quad \mbox { (by the induction hypothesis)}\\ &= \frac{1}{6}k(k+1)(2k+1) + \frac{1}{6} \cdot 6(k+1)^2\\ &= \frac{1}{6}(k+1)\left[k(2k+1)+6(k+1)\right]\\ &= \frac{1}{6}(k+1)\left(2k^2+7k+6\right)\\ &= \frac{1}{6}(k+1)(k+2)(2k+3)\\ &= \frac{1}{6}(k+1)(k+1+1)(2(k+1)+1).\end{aligned}\]

Hence by PMI we conclude that \[1^2+2^2+\cdots+n^2 = \frac{1}{6}n(n+1)(2n+1).\nonumber \] for \(n\geq 1\).

One of the hallmarks of a correctly written proof by induction is that if we check the claim by letting \(n\) equal every integer from \(n_0\) on, in turn, in \(P(n)\), the proof should give us convincing justification through a "domino" effect. For example, in the proposition above, we identified \(n_0\) as 1; does the proof justify \(P(1)\)? Yes—this is what second sentence explained.

Now does the proof justify \(P(2)\)? Consider the remainder of the proof. We start by taking as a fact that \(P(1),\cdots,P(k)\) are all true. Well, at the moment we only know that \(P(1)\) is true, so we can only suppose that \(P(1),\cdots,P(k)\) are all true if \(k=1\) and the list \(P(1),\cdots,P(k)\) really just contains \(P(1)\). So let's read the rest of the proof, substituting \(1\) everywhere we see \(k\). The remaining sentences in the proof give us a procedure for proving \(P(k+1)\), which for us means \(P(2)\). So yes, the proof does justify \(P(2)\).

Now does the proof justify \(P(3)\)? Let's return to midway through the proof and reread the proof beginning at the induction hypothesis. There we are supposed to start from the claim that \(P(1),\cdots,P(k)\) are all true. Since at this point we have been convinced that \(P(1)\) and \(P(2)\) are both true, we can now let \(k=2\) and substitute \(2\) everywhere we see \(k\). The remaining sentences in the proof then prove \(P(k+1)\), which for us at this point means \(P(3)\), so the proof does justify \(P(3)\).

Continuing this process, rereading the proof over and over, allows us to justifiably and logically let \(k\) be larger and larger in the induction hypothesis, and we see that if we reapplied the portion of the proof beginning the induction hypothesis enough times, we would have a proof of \(P(n)\) no matter which finite integer (past \(n_0\)) \(n\) happened to be. This is why induction proves that \(P(n)\) is true for any \(n \geq n_0\).

Following is another example of a proof using PMI. This time the statement \(P(n)\) is an inequality, and the value \(n_0\) is not 1. Try coming up with a proof of your own before reading the proof presented here.

Proposition \(\PageIndex{3}\)

If \(n \ge 5\) then \(2^n>5n\).

Proof

We prove the proposition by induction on the variable \(n\). If \(n=5\) we have \(2^5>5 \cdot 5\) or \(32>25\) which is true.

Assume \[2^n>5n \quad \text{ for }5 \leq n \leq k \quad \text{(the induction hypothesis)}.\nonumber \]

Taking \(n = k\) we have \[2^k>5k.\nonumber \] Multiplying both sides by 2 gives \[2^{k+1}>10k.\nonumber \] Now \(10k=5k+5k\) and \(k\geq 5\) so \(k\geq 1\) and therefore \(5k\geq 5\). Hence \[10k=5k+5k\geq 5k+5=5(k+1).\nonumber \] It follows that \[2^{k+1}>10k\geq 5(k+1)\nonumber \] and therefore \[2^{k+1}>5(k+1).\nonumber \]

Hence by PMI we conclude that \(2^n>5n\) for \(n\geq 5\).

Note that in Proposition \(\PageIndex{3}\) the condition \(n \geq 5\) (which leads to us having \(n_0=5\)) is necessary, since \(2^5 > 5\cdot 5\), but \(2^4 < 5\cdot 4\).

Considering both the previous propositions, a few general comments may help. First, note that the finished version of a proof by induction is often much more concise and straightforward than the calculations and notes that went into finding it. For that reason induction proofs in texts like this one may seem a bit more mysterious than necessary, but to most mathematicians, the conciseness is preferable, and you would do well to try to include only the necessities in your proofs when you are polishing them up.

Next, and more importantly, how did we figure out what to do to prove \(P(k+1)\) once we had supposed that \(P(n)\) was true for \(n_0\leq n \leq k\)? This is the big challenge of mathematical induction, and the one place where proofs by induction require problem solving and sometimes some creativity or ingenuity. Different steps were required at this stage of the proofs of the two propositions above, and figuring out how to show that \(P(k+1)\) automatically happens if \(P(n_0), \dots, P(k)\) do is not an exact science.

One of the best things to try is to pick out a part of the statement \(P(k+1)\) that looks like something from one of the earlier statements \(P(n_0), \cdots, P(k)\), and try to conclude something about that part of \(P(k+1)\).

In the proof of Proposition \(\PageIndex{2}\), for example, the left-hand side of \(P(k+1)\) included all the terms of the left-hand side of \(P(k)\) and one more term besides, and it was this connection to the equation \(P(k)\) that made proving \(P(k+1)\) possible. In the proof of Proposition \(\PageIndex{3}\), the inequality \(P(k+1)\) had a left-hand side that included \(2^{k+1}\). This didn't match the left-hand side of any other \(P(5), \dots, P(k)\), but it was pretty close to the \(2^k\) appearing on the left-hand side of \(P(k)\). Using the inequality \(2^k > 5k\) from \(P(k)\) to try to say something about the \(2^{k+1}\) in \(P(k+1)\) is what motivated us to multiply both sides of \(P(k)\) by 2, getting \(2^{k+1}>10k\) as we did.

This may still not completely clarify how to use earlier \(P(n)\) statements to prove \(P(k+1)\), but it's a starting point, and proving \(P(k+1)\) in PMI(b) will become much clearer and easier with practice. Again, pick out a part of the statement \(P(k+1)\) that looks like something from one of the earlier statements \(P(n)\), and try to conclude something about the rest of \(P(k+1)\).

Finally, you'll notice that there were a few things common to the proofs of Propositions \(\PageIndex{2}\) and \(\PageIndex{3}\) that were not spelled out in the simplified outline for induction proofs from before. We now give a more detailed outline for proofs by induction, followed by exercises where you can practice applying it.

Eight major parts of a proof by induction:

1. First state what proposition you are going to prove. Precede the statement by Proposition, Theorem, Lemma, Corollary, Fact, or To Prove:.
2. Write the Proof or Pf. at the very beginning of your proof.
3. Say that you are going to use induction (not every mathematical proof uses induction!) and if it is not obvious from the statement of the proposition, clearly identify \(P(n)\), i.e., the statement to be proved and the variable it depends upon, and the starting value \(n_0\). Even though this is usually clear, sometimes these things may not be obvious. And, of course, the variable need not be \(n\).
4. Prove that \(P(n)\) holds when \(n = n_0\).
5. Assume that \(P(n)\) holds for \(n_0\leq n\leq k\). (State this assumption in writing, closely following the form in the examples here!) This assumption will be referred to as the induction hypothesis.
6. Use the induction hypothesis and anything else that is known to be true to prove that \(P(n)\) holds when \(n = k + 1\).
7. Conclude, perhaps in writing, that since the conditions of the PMI have been met, \(P(n)\) holds for \(n\geq n_0\).
8. Write QED, \(\square\), \(\blacksquare\), or \(//\) or something to indicate that you have completed your proof.

Exercises

Exercise \(\PageIndex{1}\)

Consider the following statement:

Every nonnegative integer can be written as the sum of four perfect squares.

In this exercise we'll imagine what a proof of this statement by induction would look like, if one were possible.

1. For this statement, answer these questions (coming from Part 3 of the eight major parts at the end of the section): What would \(n_0\) be? What would \(P(n)\) be? (Remember that \(P(n)\) should be a statement—a complete mathematical sentence.)
2. In order to get some practice with working with \(P(n)\), use your answer in part (a) to write out the statements \(P(2)\) and \(P(5)\). (Do a thorough job—be sure to write out the complete statements.)
3. Now for Part 4 of the list: Write out the statement \(P(n_0)\) using your answer from part (a), and then prove that \(P(n_0)\) is true.
4. Carry out Part 5: Carefully write out the induction hypothesis we would use in an induction proof of the statement above, starting with the word "Assume."
5. What is the "goal" of Part 6? In other words, what is the specific statement about numbers and perfect squares we would like to show holds in this part?
6. Yes or no—is it easy to you to see how to use the facts \[\begin{aligned} 0 &= 0^2 + 0^2 + 0^2 + 0^2;& 3 &= 1^2 + 1^2 + 1^2 + 0^2;\\ 1 &= 1^2 + 0^2 + 0^2 + 0^2;& 4 &= 1^2 + 1^2 + 1^2 + 1^2;\\ 2 &= 1^2 + 1^2 + 0^2 + 0^2;& &\end{aligned}\] to write 5 as a sum of four perfect squares? Do you see how to complete Part 6 of the eight major parts, for any \(k\)? How likely do you think it is that an induction proof is possible for the statement we started with?\(^{5}\)

Exercise \(\PageIndex{2}\)

Prove that \(2^n>6n\) for \(n\geq 5\).

Exercise \(\PageIndex{3}\)

Prove that \(1+2+\cdots +n=\dfrac{n(n+1)}2\) for \(n\geq 1\).

Exercise \(\PageIndex{4}\)

Using only PMI and properties of inequalities from the previous chapter, prove that if \(0 < a < b\) then \(0 < a^n<b^n\) for all \(n \in \mathbb{N}\).

Exercise \(\PageIndex{5}\)

Prove that \(n!<n^n\) for \(n\geq 2\).

(For positive integers \(n\), we define \(n\) factorial, written \(n!\), as the product of all integers between and including \(n\) and \(1\). For example, \(1! = 1\) and \(2! = 2\cdot 1 = 2\) and \(5! = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 120\).)

Exercise \(\PageIndex{6}\)

Prove that \(1+2+2^2+\cdots +2^n=2^{n+1}-1\) for \(n \ge 1\).

Exercise \(\PageIndex{7}\)

Use PMI to prove that \(\underbrace{111\cdots 1}_{n \,1\mbox {'s}}=\dfrac{10^n-1}9\) for \(n \ge 1\).

Exercise \(\PageIndex{8}\)

Prove that if \(a\) and \(r\) are real numbers and \(r\neq 1\), then for \(n \ge 1\), \[a+ar+ar^2+\cdots +ar^n=\dfrac{a\left( r^{n+1}-1\right)}{r-1}.\nonumber \]

Exercise \(\PageIndex{9}\)

Prove that \(1^3+2^3+3^3+\cdots +n^3=\dfrac{n^2(n+1)^2}4\) if \(n\geq 1\). (Compare this result to Exercise \(\PageIndex{3}\).)

Exercise \(\PageIndex{10}\)

Prove that \(\dfrac{1}{1\cdot 2} + \dfrac{1}{2\cdot 3} + \dfrac{1}{3\cdot 4} + \cdots + \dfrac{1}{n(n+1)} = \dfrac{n}{n+1}\) for all \(n \geq 1\).

Exercise \(\PageIndex{11}\)

Perhaps imitating the steps from the "brief exploration" in this chapter, conjecture a formula for each of the sums below. Then using PMI, prove that your conjectured formula is correct.

1. \(1\cdot 2 + 2 \cdot 3 + 3 \cdot 4 + \cdots + n(n+1)\);
2. \(1 + 3 + 5 + \cdots + (2n-1)\).

Exercise \(\PageIndex{12}\)

Using induction, prove that \[a^n - b^n = (a-b)(a^{n-1}+a^{n-2}b + \cdots + ab^{n-2}+b^{n-1})\nonumber \] for all integers \(n \geq 2\). (Hint: during the induction step, write \(a^{k+1}-b^{k+1} = a^{k+1}-ab^k + ab^k-b^{k+1}\).)

Exercise \(\PageIndex{13}\)

Prove that if \(n\geq 12\) then \(n\) can be written as a sum of \(4\)'s and \(5\)'s. For example, \(23=5+5+5+4+4=3 \cdot 5+2 \cdot 4\).

(Hint: In this case it will help to do the cases \(n=12\), \(13\), \(14\), and \(15\) separately. Then use induction to handle \(n\geq 16\).)

Exercise \(\PageIndex{14}\)

1. For \(n\ge 1\), the triangular number \(t_n\) is the number of dots in a triangular array that has \(n\) rows with \(i\) dots in the \(i\)-th row. Find a formula for \(t_n\), \(n\ge 1\).
2. Suppose that for \(n \geq 1\), \(s_n\) denotes the number of dots in a square array that has \(n\) rows with \(n\) dots in each row. Find a formula for \(s_n\). The numbers \(s_n\) are usually called squares.

Exercise \(\PageIndex{15}\)

1. Find the first 10 triangular numbers and the first 10 squares.
2. Which of the triangular numbers in part (a) are also squares?
3. Can you find the next triangular number which is a square?
4. After completing parts (a)–(c), read the Wikipedia.org article "Square triangular number" and write one or more detailed sentences on what you thought of it.

Exercise \(\PageIndex{16}\)

Some propositions that can be proved by induction can also be proved without induction. Prove the propositions in Exercises \(\PageIndex{3}\) and \(\PageIndex{8}\) and \(\PageIndex{11}\)(b) without induction.

(Hints: For Exercise \(\PageIndex{3}\) write \(s=1+2+\dots+(n-1)+n\). Directly under this equation write \(s=n+(n-1)+\dots+2+1\). Add these equations to obtain \(2s = n(n+1)\). Solve for \(s\). For Exercise \(\PageIndex{8}\) write \(p=a+ar+ar^2+\dots+ar^n\). Then multiply both sides of this equation by \(r\) to get a new equation with \(rp\) as the left hand side. Subtract these two equation to obtain \(pr-p=ar^{n+1}-a\). Now solve for \(p\). For Exercise \(\PageIndex{11}\)(b), draw rows of dots as in Exercise \(\PageIndex{14}\)(b) and break them up into sets of size \(1,3,5,\dots\).

Footnotes

[1] Here we rely a bit on your previous knowledge. We will discuss primes and prime factorizations in more depth later. Note that \(1\) is not a prime.

[2] In other math courses you may have seen this principle called strong induction, with "ordinary" induction referring to a principle with a different condition (b) than the one appearing here. This should not matter too much; the PMI used here is chosen for simplicity.

[3] An example may be found in Exercise \(\PageIndex{1}\) at the end of the chapter.

[4] Depending on the details of PMI(b), sometimes in PMI(a) not only \(P(n_0)\) but also a few more specific statements \(P(i)\) (such as \(P(n_0 +1)\) or \(P(n_0 +2))\) are necessary to check in order to make the logic work; see, for example, Exercise \(\PageIndex{13}\) at the end of the chapter. Most of the induction proofs in this text will require just checking \(P(n_0)\); when more early cases are required, this will be pointed out.

[5] We leave it as an unanswered question whether the statement this exercise is based on is true, though we will come back to this question later in the text. The point of the exercise is to show that you can carry out most of the eight major parts even before you figure out how to carry out Part 6 (or even before you know whether the statement you are attempting to prove is even true!).