1.13: The Gaussian Integers
- Page ID
- 93796
In this section we study a special subset of the complex numbers known as the Gaussian integers.
A Gaussian integer is a complex number of the form \(a+bi\) where both \(a\) and \(b\) are integers. We often denote the set of Gaussian integers by \(\mathbb{Z}[i]\).
In order to simplify notation (and not confuse Gaussian integers with ordinary integers), we will sometimes use Greek letters \(\alpha, \beta\), etc. to represent Gaussian integers.
The Gaussian integers have many special properties that are similar to those of the integers. In this chapter, once we have a few fundamental concepts, we will see how the Gaussian integers satisfy a division algorithm and a version of unique factorization. We will also see the Gaussian integers pop up a few times in later chapters.
We start with a graphical representation. Just as the integers form points along the standard real line,

we can visualize the Gaussian integers as regularly spaced points, though in a new context.
The complex numbers can be represented by a 2-dimensional drawing called an Argand plane. Just like a normal Cartesian plane, an Argand plane contains a horizontal axis and a vertical axis for measurements. However, instead of representing an ordered pair of real numbers, each point in the Argand plane represents a single complex number—the point located at what would traditionally be labeled \((x,y)\) in Cartesian coordinates instead represents the complex number \(x+yi\), where \(i\) is a square root of \(-1\), as usual. Shown here is a picture of the Argand plane:
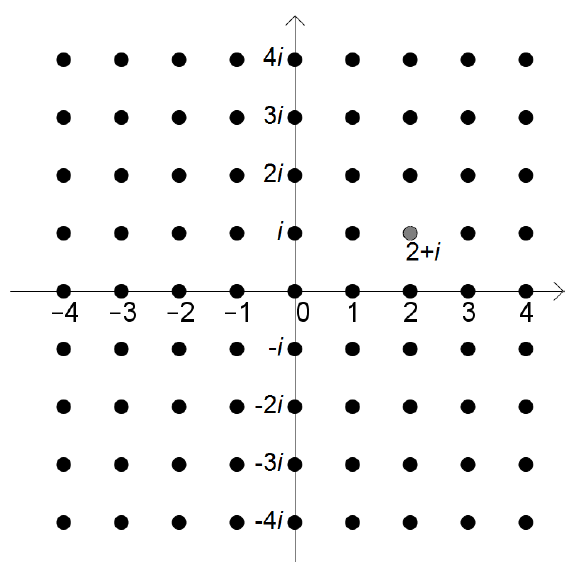
The solid points mark the locations of the Gaussian integers. Note that the horizontal axis measures the real part of each complex number, and the vertical axis measures the imaginary part. Hence the point \(2+i\) is located 2 units horizontally to the right of the center and one unit vertically up.
Since the (real) integers lie on a single line, it is easy to understand whether one integer is “bigger” than another. For the Gaussian integers, though, it is not immediately clear whether \(2+i\) is bigger or smaller than 3. Because being able to compare Gaussian integers will be important to us shortly, we will define a way to do this.
The norm of a Gaussian integer \(\alpha = a+bi\), denoted \(N(\alpha)\) or \(N(a+bi)\), is a real number defined by \[N(\alpha) = N(a+bi)=a^2+b^2.\nonumber \]
Since the norm of a Gaussian integer is a real number, we can use norms to compare “sizes” of Gaussian integers. For example, \(N(2+i) = 5\) and \(N(3) = 9\) (since \(3 = 3+0i\)), so intuitively we can think of \(2+i\) as smaller than 3. Indeed, you might notice that \(N(a+bi)\) is the square of the usual straight-line distance from \(0\) to \(a+bi\) if we think of them as the Cartesian points \((0,0)\) and \((a,b)\). For instance \(1\), \(-1\), \(i\), and \(-i\) are each one unit away from \(0\), and \(N(1)=N(-1)=N(i)=N(-i) = 1= 1^2\).
One idea you may remember from earlier exposure to complex numbers is that of a complex conjugate.
Given a complex number \(\alpha=a+bi\), the (complex) conjugate is the complex number \(a-bi\), i.e., the complex number obtained by changing the sign on the imaginary part. We denote the conjugate of \(\alpha\) with a horizontal bar above the number, so \(\overline{\alpha}=\overline{a+bi} = a-bi\).
Note that \(\overline{a-bi} = a+bi\), too, so the conjugate of a conjugate is again the original complex number. Note also that the conjugate of a real number is itself.
Some useful observations connect norms and conjugates. In the following, remember how complex numbers are multiplied: \[\begin{aligned} (a+bi)(c+di) &= ac + adi + bci + bdi^2\\ &= (ac-bd)+(ad+bc)i,\end{aligned}\] since \(i^2=-1\).
For any \(\alpha \in \mathbb{Z}[i]\) we have the following:
- \(N(\alpha) = \alpha\cdot \overline{\alpha}\);
- \(N\left(\overline{\alpha}\right) = N(\alpha)\).
Proof
Perhaps the most important property about norms is the following.
[lem: multiplicative norms] For any \(\alpha,\beta \in \mathbb{Z}[i]\), \[N\left(\alpha\beta\right) = N(\alpha)N(\beta).\nonumber \]
Proof
Divisibility and division
We can make many of the same definitions for Gaussian integers as we have done in earlier chapters for integers.
Given Gaussian integers \(\alpha\) and \(\beta\), we will say that \(\alpha\) divides \(\beta\) if there exists another Gaussian integer \(\gamma\) such that \(\alpha \gamma = \beta\). In this case we call \(\alpha\) a divisor of \(\beta\), and \(\beta\) a multiple of \(\alpha\).
If \(p\) and \(q\) are (real) integers, then it can be shown that \(p\) divides \(q\) under this new definition of “divides” if and only if \(p|q\) as integers.
It may seem a little difficult at first to decide whether one Gaussian integer divides another. For example, how would you know whether \(1-i\) divides 4, or whether \(2+i\) divides 6? As a corollary to Lemma \(\PageIndex{2}\), we can find a quick way to rule out certain possibilities.
If \(N(\alpha)\) does not divide \(N(\beta)\), then \(\alpha\) is not a divisor of \(\beta\).
Since \(N(2+i) = 5\) and \(N(6)=36\) and \(5\) is not a divisor of 36, we know that \(2+i\) does not divide 6.
However, is \(1-i\) a divisor of 4? Comparing their norms
\[\begin{gathered} N(1-i) = 1^2+(-1)^2 = 2,\\ N(4) = 4^2+0^2 = 16,\end{gathered}\]
we do see that \(2\) divides \(16\). Neither Corollary \(\PageIndex{1}\) nor Lemma \(\PageIndex{2}\) guarantees that \(1-i\) divides \(4\); it still might not. If it did, how could we find a number to multiply \(1-i\) by to produce 4?
At this point, though we have tried to avoid much use of fractions in this text, we will find it convenient to use them. The number we seek is \[\frac{4}{1-i},\nonumber \] but this complex number isn’t written in our usual form of \(a+bi\); how can we put it in this form?
You may remember the answer from past experience with complex numbers: to put a complex fraction with a non-real denominator in the form \(a+bi\), we multiply both the numerator and denominator by the conjugate of the denominator.
In this case, we find \[\frac{4}{1-i} = \frac{4}{1-i}\cdot \frac{1+i}{1+i} = \frac{4+4i}{1^2-i^2} = \frac{4}{2} + \frac{4i}{2} = 2 + 2i.\nonumber \]
Since \(2+2i\) is a Gaussian integer and \((1-i)(2+2i) = 4\), we conclude that yes, \(1-i\) is a divisor of \(4\). (If the quotient had turned out to be a complex number other than a Gaussian integer, then we would have concluded that \(1-i\) wasn’t a divisor.)
Now that we have defined divisors, we need a few more definitions that weren’t important when working with integers but will be useful now.
A unit in \(\mathbb{Z}[i]\) is an element \(\omega\) for which \(N(\omega)=1\). Two Gaussian integers \(\alpha\) and \(\beta\) are associates if there exists a unit \(\omega\) such that \(\alpha \omega = \beta\).
Note that if \(v+wi\) is a unit in \(\mathbb{Z}[i]\), then \(v\) and \(w\) are integers, and \(v^2+w^2 = 1\). The only ways this can happen is if one of \(v\) or \(w\) is \(\pm 1\) and the other is 0. Thus the only units in \(\mathbb{Z}[i]\) are \(1\), \(-1\), \(i\), and \(-i\). Consequently, each Gaussian unit has a total of four associates (counting itself).
The Gaussian integer \(2+3i\) has four associates: itself, and \[\begin{aligned} (2+3i)(-1) &= -2-3i,\\ (2+3i)i &= -3 + 2i, \text{ and}\\ (2+3i)(-i) &= 3 - 2i.\end{aligned}\]
Associates play an important role in statements about divisibility, because of the next lemma.
Let \(\alpha\), \(\beta\), and \(\gamma\) be Gaussian integers.
- If \(\alpha\) and \(\beta\) are associates, then \(\gamma\) divides one of \(\alpha,\beta\) if and only if it divides the other.
- If \(\alpha\) and \(\beta\) are associates, then \(\alpha\) divides \(\gamma\) if and only if \(\beta\) divides \(\gamma\).
Now what can we say for Gaussian integers like \(2+i\) and \(6\) where neither divides the other? As we did for the integers, we introduce a Division Algorithm-type theorem for the Gaussian integers.
Given Gaussian integers \(\alpha\) and \(\beta\), where \(\beta \neq 0\), there exist Gaussian integers \(\kappa\) and \(\rho\) such that \[\alpha = \beta\kappa+\rho \qquad \text{ and } \qquad 0 \leq N(\rho) < N(\beta).\nonumber \]
For the sake of brevity, and because the details are in some respects analogous to those in the proof of the Division Algorithm, we will skip the proof of Theorem \(\PageIndex{1}\). However, we will illustrate some of its ideas in the following example.
We will find \(\kappa\) and \(\rho\) given \(\alpha = 6\) and \(\beta = 2+i\). We start with \(\kappa\) by computing the complex number \[\frac{\alpha}{\beta}=\frac{6}{2+i} = \frac{6}{2+i}\cdot \frac{2-i}{2-i} = \frac{12-6i}{2^2 - (-1)^2} = \frac{12}{5} - \frac{6}{5}i.\nonumber \] The answer is not a Gaussian integer, as \(\kappa\) should be, so we will round both the real and imaginary parts to the nearest integer and set \(\kappa\) equal to the result, obtaining here \(\kappa = 2 - i\).
We now find \(\rho = \alpha - \beta\kappa\): \[\rho = 6 - (2+i)(2-i) = 6 - 5 = 1.\nonumber \] We check that the norms work as they should, and we see that indeed, \[0 \leq N(\rho) = N(1) = 1 < 5 = N(2+i) = N(\beta).\nonumber \]
In general, finding a quotient and remainder when one Gaussian integer is divided by another can be accomplished just as in the previous example—we treat the Gaussian integers as complex numbers and divide as normal, producing a complex number with possibly non-integer coeffients for real and imaginary parts. Rounding these numbers to the nearest integer will provide a quotient, which can then be used to compute the remainder. Note that as opposed to the Division Algorithm, here we don’t require a nonnegative remainder, and we don’t claim that the quotient and remainder are unique. The next example illustrates why.
If we attempt to find a quotient and remainder for the Gaussian integers \(1+i\) and \(3i\) using the same process as in the last example, we find \[\begin{gathered} 3i = (1+i)(2+2i) - i,\\ 0 \leq N(-i) < N(1+i); \end{gathered}\] or \[\begin{gathered} 3i = (1+i)(1+i) + i,\\ 0 \leq N(i) < N(1+i); \end{gathered}\] or perhaps \[\begin{gathered} 3i = (1+i)(1+2i) + 1,\\ 0 \leq N(1) < N(1+i);\\ \end{gathered}\] or \[\begin{gathered} 3i = (1+i)(2+i) - 1,\\ 0 \leq N(-1) < N(1+i); \end{gathered}\] since at the first step when we divide \(3i\) by \(1+i\) the fraction \(3i/(1+i)\) is equal to \(3/2 + (3/2)i\), and \(3/2\) is equally close to 1 and to 2.
Greatest common divisors
Now that we have a Gaussian integer version of the Division Algorithm, can we adapt some of our earlier algorithms, like the Euclidean Algorithm? What would the outcome tell us? Let’s try.
If we begin the Euclidean Algorithm with \(2-3i\) and \(3+5i\), we may obtain \[\begin{aligned} 3+5i &= (2-3i)(-1+i) + 2;\\ 2-3i &= 2(1-2i) + i;\\ 2 &= i(-2i) + 0. \end{aligned}\] The last nonzero remainder is \(i\).
If the numbers involved in the Euclidean Algorithm were integers, we would interpret the last nonzero remainder to be the greatest common divisor. Can we do the same for Gaussian integers?
Yes, if we take the right meaning for the word “greatest”. As in the proof of the Euclidean Algorithm, a Gaussian integer is a common divisor of \(3+5i\) and \(2-3i\) if and only if it is a common divisor of \(2-3i\) and \(2\), which happens if and only if it is a common divisor of \(2\) and \(i\), which happens if and only if it is a common divisor of \(i\) and \(0\). Thus the common divisors all divide \(i\), so \(i\) is the “greatest” common divisor in the sense that every common divisor divides it.
By Lemma \(\PageIndex{3}\), a Gaussian integer divides \(i\) if and only if it divides \(1\), \(-1\), or \(-i\), so these four associates are all greatest common divisors of \(3+5i\) and \(2-3i\).
In general, carrying out the Euclidean Algorithm with Gaussian integers will always produce a greatest common divisor, and we may find others by considering associates.
Unique factorization
Studying the divisors of integers led us to think about prime numbers, those integers that could not be divided evenly by any smaller positive integers other than 1. We then saw that every positive integer greater than 1 could be written uniquely as a product of these primes, if we ordered the primes from smallest to largest. We can study similar questions for the Gaussian integers, though the answers will be different at times.
An element in \(\mathbb{Z}[i]\) is called a Gaussian prime if it cannot be written as the product of two or more other Gaussian numbers where none of the numbers in the product is a unit.
The numbers \(11-10i\) and \(27\) are not Gaussian primes, since \(11-10i=(2-3i)(4+i)\) and \(27 = 3\cdot 9=(3+0i)(9+0i)\).
In contrast, \(2+i\) is a Gaussian prime. To see why, suppose to the contrary that \(2+i= \alpha\beta\), where \(\alpha,\beta \in \mathbb{Z}[i]\) and neither is a unit. By Lemma \(\PageIndex{2}\), \[N(\alpha) N(\beta) = N(2+i) = 5.\nonumber \] Since \(N(\alpha)\) and \(N(\beta)\) are both nonnegative integers, one must equal 5 and the other must equal 1. However, if either \(\alpha\) or \(\beta\) has a norm of 1 then it is a unit, contrary to our assumption. Thus \(2+i\) is a Gaussian prime.
By the same reasoning as in the example above, we can say the following.
For every \(\alpha \in \mathbb{Z}[i]\), if \(N(\alpha)\) is a prime number, then \(\alpha\) is a Gaussian prime.
Note that the converse of Proposition \(\PageIndex{1}\) isn’t true; for example, the norm of \(3\) is \(9\), is composite, but \(3\) is still a Gaussian prime (see Exercise \(\PageIndex{6}\)).
The number 41 is a prime number; is it also a Gaussian prime?
If not, then there exist Gassian integers \(\alpha\) and \(\beta\) whose product is 41, such that neither is a unit. By Lemma \(\PageIndex{2}\), \[N(\alpha) N(\beta) = N(41) = 41^2.\nonumber \] This forces \(N(\alpha) = 41\) and \(N(\beta)=41\). Can we find two Gaussian integers with norm 41 whose product is 41?
We can! Observe that \(4+5i\) and \(4-5i\) both have norm 41, and \((4+5i)(4-5i)=41\). Hence 41, though a prime number, is not a Gaussian prime.
Many other prime numbers are not Gaussian primes (see Exercise \(\PageIndex{6}\)), though some, like 3, are prime in both the integers and in the Gaussian integers. We will be able to say more about primes and Gaussian primes in the exercises of Section 1.28.
Now that we have the notion of Gaussian primes, can we factor Gaussian integers uniquely into Gaussian primes? At first glance, the answer might seem to be no.
In the previous example we saw that \[41 = (4+5i)(4-5i).\nonumber \] Since \(N(4+5i)\) and \(N(4-5i)\) are prime numbers, we know by Proposition \(\PageIndex{1}\) that \(4+5i\) and \(4-5i\) are Gaussian primes.
However, we may also write \[41 = (5+4i)(5-4i),\nonumber \] and \(5+4i\) and \(5-4i\) are also Gaussian primes. This means that \(41\) cannot be written uniquely as a product of non-unit Gaussian primes.
Still, the numbers \(4\pm 5i\) and \(5\pm 4i\) are related. Note that \((4+5i)(-i) = 5-4i\), and \((4-5i)i = 5+4i\), so \(4+5i\) and \(5-4i\) are associates, as are \(4-5i\) and \(5+4i\). We can also derive one factorization from the other: \[\begin{aligned} 41 &= (4+5i)(4-5i) \cdot 1\\ &= (4+5i)(4-5i) \cdot (-i)i\\ &= [(4+5i)(-i)][(4-5i)i]\\ &= (5-4i)(5+4i). \end{aligned}\] Because \(-i\) and \(i\) multiply to 1, or because \(4\pm 5i\) and \(5\mp 4i\) are associates, couldn’t we say that the two factorizations are pretty much the same?
In fact, one can show that if \(\alpha\) is a Gaussian prime, then \(\omega\alpha\) is a Gaussian prime for any unit \(\omega\), so by using units whose product is 1 as in the example above, we can find many different-looking factorizations of a Gaussian integer into Gaussian primes.
Still, what if we relax our notion of “sameness” in factorizations so as to ignore differences in associates? Then the Gaussian integers can be uniquely factored into Gaussian primes.
Any Gaussian integer \(\alpha\) with norm greater than 1 can be factored into Gaussian primes, and the factorization is unique in the following sense: if \[\alpha = \beta_1\beta_2\cdots \beta_k= \gamma_1\gamma_2\cdots \gamma_\ell,\nonumber \] where each \(\beta_i\) and each \(\gamma_i\) is a Gaussian prime, then \(k=\ell\) (i.e., the numbers of primes involved are the same) and the primes may be reordered and renumbered so that \(\beta_i\) is an associate of \(\gamma_i\) for all \(i\).
We will not prove this theorem here, though you are encouraged to attempt it. Proving the existence of a prime factorization can be done by induction in much the same way that Lemma 1.12.4 uses; try to adapt Lemma 1.12.5 for the rest.
We have seen how many of the key results we have encountered so far have analogues in the number system of the Gaussian integers. Though as the text progresses, we will mention the Gaussian integers only a few more times, you are invited to think about how each new result would look if the integers involved were replaced by Gaussian integers. Doing so will lead you to research questions; it may also give you a new perspective on things you’ve already long since known.
Exercises
Prove both statements in Lemma \(\PageIndex{1}\).
Prove Lemma \(\PageIndex{2}\).
Prove both statements in Lemma \(\PageIndex{3}\).
(Hint: Recall that the only units in \(\mathbb{Z}[i]\) are \(\pm 1\) and \(\pm i\).)
Write \(i\) as a linear combination of \(2-3i\) and \(3+5i\).
(Hint: apply a method from Section 1.10 and perhaps refer to Example \(\PageIndex{5}\). Remember that the coefficients on \(2-3i\) and \(3+5i\) must be Gaussian integers; they cannot involve fractions.)
Use the Euclidean Algorithm to find a greatest common divisor of 5 and \(1-i\). Then write this greatest common divisor as a linear combination of \(5\) and \(1-i\).
(Hint: See hints from the previous exercise.)
- Show that none of \(2\), \(5\), \(13\), or \(-3+4i\) is a Gaussian prime by writing each as a product of non-unit Gaussian integers.
(Hint: \(-3+4i\) is a perfect square.) - Show that \(3\) is a Gaussian prime.
(Hint: suppose that \(a+bi\) and \(c+di\) are non-unit Gaussian integers whose product is 3, and conclude that each must have norm 3; then show that no Gaussian integer has norm 3.)
- Prove that \(1+i\) is a Gaussian prime.
- Prove that \(N(\alpha)\) is even if and only if \(\alpha\) is a multiple of \(1+i\).
- Find a Gaussian prime factorization of \(7+9i\). (Hint: get an idea from Exercise \(\PageIndex{7}\)).
- Find at least two more factorizations of \(7+9i\) into Gaussian primes, so that no Gaussian prime factor is repeated among the factorizations in part (a) and here.
The set \(\mathbb{Z}[i]\) of Gaussian integers is a number system that, like \(\mathbb{Z}\), has unique factorizations (up to associates). In this exercise we’ll consider a slightly different number system.
Define \[\mathbb{Z}[\sqrt{-5}] = \{a+b\sqrt{-5}\,\mid\, a,b \in \mathbb{Z}\}.\nonumber \] It turns out that if we define a new norm by \(N(a+b\sqrt{-5}) = a^2+5b^2\), then \(N(\alpha\beta)=N(\alpha)N(\beta)\) for every pair of elements \(\alpha,\beta \in \mathbb{Z}[\sqrt{-5}]\).
- Show that \(2\), \(23\), and \(1+3\sqrt{-5}\) are all “primes” in \(\mathbb{Z}[\sqrt{-5}]\), i.e., that they cannot be written as products of factors all having smaller norms.
(Hint: Use the multiplicative property of the norm and a proof by contradiction as in Example \(\PageIndex{6}\). As part of your answer, show that \(a^2+5b^2\) never equals \(2\) or \(23\) when \(a\) and \(b\) are integers.) - Show that \(1+3\sqrt{-5}\) divides \(46\) in \(\mathbb{Z}[\sqrt{-5}]\).
- Show that \(\mathbb{Z}[\sqrt{-5}]\) does not have a unique factorization property.
(Hint: Show that \(46\) does not have a unique factorization into the primes in \(\mathbb{Z}[\sqrt{-5}]\).)


