4.1: Some Speculative History
- Page ID
- 77011
\(\newcommand{\RR}{\mathbb R}\)
\(\newcommand{\QQ}{\mathbb Q}\)
\(\newcommand{\ZZ}{\mathbb Z}\)
\(\newcommand{\Cc}{\mathcal C}\)
\(\newcommand{\Dd}{\mathcal D}\)
\(\newcommand{\Ee}{\mathcal E}\)
\(\newcommand{\Ff}{\mathcal F}\)
\(\newcommand{\Kk}{\mathcal K}\)
\(\newcommand{\Mm}{\mathcal M}\)
\(\newcommand{\Pp}{\mathcal P}\)
\(\newcommand{\ind}{\operatorname{ind}}\)
\(\newcommand{\ord}{\operatorname{ord}}\)
Perhaps there was a form of deception that preceded language – certainly many a house pet has feigned innocence despite the clear evidence of involvement in stealing treats. And even apiologists may not know if some lazy bees make up a story about a long excursion to a new flower patch when their Queen demands an accounting.
But among homo sapiens, probably as soon as there was language, there was lying. Of course, when two humans are face to face, both parties have some control, such as: the listener can make an attempt to evaluate the trustworthiness of speaker, they can both form their own judgements of the other’s identity and therefore choose what they wish to share with each other, and the words of the speaker pass directly from their lips to the listener’s ears without the possibility of change of meaning in flight (absent considerations of ambient noise and so on).
A great deal changed with the invention of writing more than 5000 years ago. Words frozen in physical form, and the ideas they represent, can be taken and shared with a wide range of parties other than those with whom the original author wanted to communicate. In addition, if an author is not able to hand her work directly to the intended reader and instead the written words are out in the world on their own for a while, then both intended communicants can no longer be sure that the other is who the writing claims them to be nor that the writing remains the unchanged symbols that the other party originally set down.
Let us formalize some of these issues of information security (as it is called now), in the context of a message to be sent from someone named Alice to someone named Bob. The role of the possibly disruptive and overly intrusive environment is played in our little drama by Eve. (Traditionally one skips directly to a character whose name starts with E to symbolize both the environment and also someone who is potentially an eavesdropper1.)
Here is some basic terminology:
Definition: Confidentiality
Confidentiality means that only the intended recipient can extract the content of the message – Alice wants only Bob to get her message and not Eve, no matter if she listens on the eavesdrop or intercepts the message as it travels in some form from Alice to Bob.
Definition: Integrity
Message integrity means that the recipient can be sure the message was not altered – Bob wants to know that what he gets is what Alice wrote, not what the mischievous Eve intended to change it into.
Definition: Authentication
Sender authentication means that the recipient can determine from the message the identity of the sender – Bob wants to be sure this message did in fact originate with Alice.
Definition: Non-repudiation
Sender non-repudiation means that the sender should not be able to deny sending that message – Bob wants to be able to hold Alice to her promises.
Note that Alice and Bob may actually be the same person sending a message from a past self to their future self. For example, someone may want to keep records which must be confidential and whose integrity must be reliable, even if there is a break-in to the site keeping those records.
One of the earliest schemes attempting to achieve confidentiality was probably used around the \(7^{\text{th}}\) century BCE in Greece by military commanders who wanted to get dispatches from far away soldiers, and to send them orders, in a way that even if the messenger is captured, the message they carry will not be readable by the enemy. They used a device called a scytale (the “c” is hard and the word rhymes with “Italy”), which was a cylindrical stick – maybe a spear shaft – (\(\sigma\kappa\upsilon\tau\acute{\alpha}\eta\) means baton in ancient Greek), around which a long strip of parchment was wrapped in a spiral.
A message could then be written in parallel rows along the length of the scytale, so that when the strip was unwound, the letters were all jumbled and the message was unreadable.
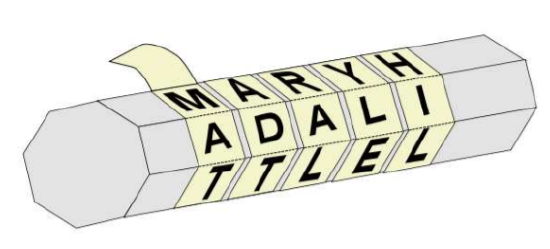
On the other end, assuming the receiver also has a scytale, when the strip is wound in a spiral and read lengthwise, the message reappears, as if by magic.
Before we go on, a few more technical terms:
Definition: Plaintext
The message that Alice wishes to send to Bob, in its actual original (and final) form is called the plaintext.
Definition: Encryption Cipher
An algorithm that Alice uses to transform (obfuscate) the plaintext into a form that will remain confidential even if observed by Eve while in flight is called a cipher. We also say that Alice encrypts the (plaintext) message.
Definition: Ciphertext
After the message has been encrypted, it is called the ciphertext.
Definition: Decrypt
When Bob receives the ciphertext, he applies another algorithm to decrypt it and recover the plaintext.
Graphically:
Basic crypto terminology:
| Alice | on public network | Bob |
| plaintext/cleartext | ||
| message \(m\) | ||
| encrypts \(m\) to \(c\) | ||
| transmits \(c\) | \(\rightarrowtail\; \; \;\)ciphertext \(c\; \; \; \rightarrowtail\) | receives \(c\) |
| decrypts \(c\) to | ||
| recover plaintext \(m\) |
Suppose a spy sees scouts in the field wrapping strips of parchment around their spears and writing down the length of the spear: meaning Eve learns the encryption algorithm. Although the algorithm is known, confidentiality may be preserved:
Definition: Key
Additional information (some of which is) used in encryption and (some of) which is necessary for successful decryption is called a key.
In the case of encryption with a scytale, the diameter of the scytale is the key. In fact, there is some conjecture that the scytale was also a simple from of authentication: only Alice had the matching scytale to the Bob’s, so if Bob could read any coherent sequence of letters at all along his scytale, he knew Alice had sent it.
Even with a key, the vulnerabilities of this cryptosystem are fairly clear. And Athens did lose the Peloponnesian War.
Many hundreds of years of cryptology have shown that in fact it is better to reveal the algorithms of your cryptosystem to the public, and only to keep the key for a particularly communication channel (between Alice and Bob, say) secret. There are many reasons for this, the primary one probably being that the author of a cryptosystem can never be sure they have thought of all the possible methods of cryptanalysis which will be used against it. So the system’s author is better off letting the general crypto community do its best against the system, and only the systems which have withstood such assault should be used. After all, this is basic to the scientific method itself: scientists publish all the details of their experiments, so others can try them as well and give independent verification or find something to criticize.
This idea – that the security of a cryptosystem should be based on the secrecy of the key but not of the algorithm – has come to be called Kerckhoff’s Principle, after a set of cryptosystem design ideas written down in 1883 by a French military cryptography. It is held in opposition to cryptosystems, thought of as very weak, which rely upon no one ever finding out the algorithms: such systems rely instead on the ill-advised security through obscurity paradigm.
Exercise \(\PageIndex{1}\)
- Suppose for some \(k\in\NN\), the cleartext Alice wishes to send consists of some symbols \(m_1,\dots,m_k\). Assume that the scytale she uses has a diameter such that \(s\in\NN\) letters can be written on each turn of the spiral of parchment, when it is wrapped around the scytale.
- Write one or more formulæ describing what the letters \(c_1,\dots,c_k\) of the ciphertext will be. You should assume \(s<k\) and, if you like, that they have any particular useful relationship such as \(s\mid k\).
- Even if the scytale cryptosystem were strong, there may be problems using it for authentication. Describe how authentication might fail depending upon the message being sent – give an example or two of “bad” messages for authentication.
- The scytale cryptosystem seems weak. Describe how you would cryptanalyze it.


