2.6: Integrating Factors
- Page ID
- 9402
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
In the previous section on Exact Equations we saw that if \(M\), \(N\), \(M_y\) and \(N_x\) are continuous and \(M_y=N_x\) on an open rectangle \(R\) then
\[\label{eq:2.6.1} M(x,y)\,dx+N(x,y)\,dy=0\]
is exact on \(R\). Sometimes an equation that isn’t exact can be made exact by multiplying it by an appropriate function. For example,
\[\label{eq:2.6.2} (3x+2y^2)\,dx+2xy\,dy=0\]
is not exact, since \(M_y(x,y)=4y\ne N_x(x,y)=2y\) in Equation \ref{eq:2.6.2}. However, multiplying Equation \ref{eq:2.6.2} by \(x\) yields
\[\label{eq:2.6.3} (3x^2+2xy^2)\,dx+2x^2y\,dy=0,\]
which is exact, since \(M_y(x,y)=N_x(x,y)=4xy\) in Equation \ref{eq:2.6.3}. Solving Equation \ref{eq:2.6.3} by the procedure given in Section 2.5 yields the implicit solution
\[x^3+x^2y^2=c.\nonumber \]
A function \(\mu=\mu(x,y)\) is an integrating factor for Equation \ref{eq:2.6.1} if \[\label{eq:2.6.4} \mu(x,y)M (x,y)\,dx+\mu(x,y)N (x,y)\,dy=0\] is exact. If we know an integrating factor \(\mu\) for Equation \ref{eq:2.6.1}, we can solve the exact equation Equation \ref{eq:2.6.4} by the method of Section 2.5. It would be nice if we could say that Equation \ref{eq:2.6.1} and Equation \ref{eq:2.6.4} always have the same solutions, but this isn’t so. For example, a solution \(y=y(x)\) of Equation \ref{eq:2.6.4} such that \(\mu(x,y(x))=0\) on some interval \(a<x<b\) could fail to be a solution of \ref{eq:2.6.1} (Exercise 2.6.1)
Finding Integrating Factors
By applying Theorem 2.5.2 (with \(M\) and \(N\) replaced by \(\mu M\) and \(\mu N\)), we see that Equation \ref{eq:2.6.4} is exact on an open rectangle \(R\) if \(\mu M\), \(\mu N\), \((\mu M)_y\), and \((\mu N)_x\) are continuous and \[{\partial\over\partial y}(\mu M)={\partial\over\partial x} (\mu N) \quad \text{or, equivalently,} \quad \mu_yM+\mu M_y=\mu_xN+\mu N_x\nonumber \] on \(R\). It’s better to rewrite the last equation as \[\label{eq:2.6.5} \mu(M_y-N_x)=\mu_xN-\mu_yM,\] which reduces to the known result for exact equations; that is, if \(M_y=N_x\) then Equation \ref{eq:2.6.5} holds with \(\mu=1\), so Equation \ref{eq:2.6.1} is exact.
You may think Equation \ref{eq:2.6.5} is of little value, since it involves partial derivatives of the unknown integrating factor \(\mu\), and we haven’t studied methods for solving such equations. However, we’ll now show that Equation \ref{eq:2.6.5} is useful if we restrict our search to integrating factors that are products of a function of \(x\) and a function of \(y\); that is, \(\mu(x,y)=P(x)Q(y)\). We’re not saying that every equation \(M\,dx+N\,dy=0\) has an integrating factor of this form; rather, we are saying that some equations have such integrating factors.We’llnow develop a way to determine whether a given equation has such an integrating factor, and a method for finding the integrating factor in this case.
If \(\mu(x,y)=P(x)Q(y)\), then \(\mu_x(x,y)=P'(x)Q(y)\) and \(\mu_y(x,y)=P(x)Q'(y)\), so Equation \ref{eq:2.6.5} becomes
\[\label{eq:2.6.6} P(x)Q(y)(M_y-N_x)=P'(x)Q(y)N-P(x)Q'(y)M,\] or, after dividing through by \(P(x)Q(y)\),
\[\label{eq:2.6.7} M_y-N_x={P'(x)\over P(x)}N-{Q'(y)\over Q(y)}M.\] Now let \[p(x)={P'(x)\over P(x)} \quad \text{and} \quad q(y)={Q'(y)\over Q(y)},\nonumber \] so Equation \ref{eq:2.6.7} becomes
\[\label{eq:2.6.8} M_y-N_x=p(x)N-q(y)M.\]
We obtained Equation \ref{eq:2.6.8} by assuming that \(M\,dx+N\,dy=0\) has an integrating factor \(\mu(x,y)=P(x)Q(y)\). However, we can now view Equation \ref{eq:2.6.7} differently: If there are functions \(p=p(x)\) and \(q=q(y)\) that satisfy Equation \ref{eq:2.6.8} and we define
\[\label{eq:2.6.9} P(x)=\pm e^{\int p(x)\,dx}\quad \text{and} \quad Q(y)=\pm e^{\int q(y)\,dy},\]
then reversing the steps that led from Equation \ref{eq:2.6.6} to Equation \ref{eq:2.6.8} shows that \(\mu(x,y)=P(x)Q(y)\) is an integrating factor for \(M\,dx+N\,dy=0\). In using this result, we take the constants of integration in Equation \ref{eq:2.6.9} to be zero and choose the signs conveniently so the integrating factor has the simplest form.
There’s no simple general method for ascertaining whether functions \(p=p(x)\) and \(q=q(y)\) satisfying Equation \ref{eq:2.6.8} exist. However, the next theorem gives simple sufficient conditions for the given equation to have an integrating factor that depends on only one of the independent variables \(x\) and \(y\), and for finding an integrating factor in this case.
Let \(M,\) \(N,\) \(M_y,\) and \(N_x\) be continuous on an open rectangle \(R.\) Then:
(a) If \((M_y-N_x)/N\) is independent of \(y\) on \(R\) and we define \[p(x)={M_y-N_x\over N}\nonumber \] then \[\label{eq:2.6.10} \mu(x)=\pm e^{\int p(x)\,dx}\] is an integrating factor for \[\label{eq:2.6.11} M(x,y)\,dx+N(x,y)\,dy=0\] on \(R.\)
(b) If \((N_x-M_y)/M\) is independent of \(x\) on \(R\) and we define \[q(y)={N_x-M_y\over M},\nonumber \] then \[\label{eq:2.6.12} \mu(y)=\pm e^{\int q(y)\,dy}\] is an integrating factor for Equation \ref{eq:2.6.11} on \(R.\)
- Proof
-
(a) If \((M_y-N_x)/N\) is independent of \(y\), then Equation \ref{eq:2.6.8} holds with \(p=(M_y-N_x)/N\) and \(q\equiv0\). Therefore \[P(x)=\pm e^{\int p(x)\,dx}\quad\text{ and}\quad Q(y)=\pm e^{\int q(y)\,dy}=\pm e^0=\pm1,\nonumber \] so Equation \ref{eq:2.6.10} is an integrating factor for Equation \ref{eq:2.6.11} on \(R\).
(b) If \((N_x-M_y)/M\) is independent of \(x\) then eqrefeq:2.6.8 holds with \(p\equiv0\) and \(q=(N_x-M_y)/M\), and a similar argument shows that Equation \ref{eq:2.6.12} is an integrating factor for Equation \ref{eq:2.6.11} on \(R\).
The next two examples show how to apply Theorem 2.6.1 .
Find an integrating factor for the equation \[\label{eq:2.6.13} (2xy^3-2x^3y^3-4xy^2+2x)\,dx+(3x^2y^2+4y)\,dy=0\] and solve the equation.
Solution
In Equation \ref{eq:2.6.13} \[M=2xy^3-2x^3y^3-4xy^2+2x,\ N=3x^2y^2+4y,\nonumber \] and \[M_y-N_x=(6xy^2-6x^3y^2-8xy)-6xy^2=-6x^3y^2-8xy,\nonumber \] so Equation \ref{eq:2.6.13} isn’t exact. However, \[{M_y-N_x\over N}=-{6x^3y^2+8xy\over 3x^2y^2+4y}=-2x\nonumber \] is independent of \(y\), so Theorem 2.6.1 (a) applies with \(p(x)=-2x\). Since \[\int p (x)\,dx=-\int 2x\,dx=-x^2,\nonumber \] \(\mu(x)=e^{-x^2}\) is an integrating factor. Multiplying Equation \ref{eq:2.6.13} by \(\mu\) yields the exact equation \[\label{eq:2.6.14} e^{-x^2}(2xy^3-2x^3y^3-4xy^2+2x)\,dx+ e^{-x^2}(3x^2y^2+4y)\,dy=0.\]
To solve this equation, we must find a function \(F\) such that \[\label{eq:2.6.15} F_x(x,y)=e^{-x^2}(2xy^3-2x^3y^3-4xy^2+2x)\] and \[\label{eq:2.6.16} F_y(x,y)=e^{-x^2}(3x^2y^2+4y).\] Integrating Equation \ref{eq:2.6.16} with respect to \(y\) yields \[\label{eq:2.6.17} F(x,y)=e^{-x^2}(x^2y^3+2y^2)+\psi(x).\] Differentiating this with respect to \(x\) yields \[F_x(x,y)=e^{-x^2}(2xy^3-2x^3y^3-4xy^2)+\psi'(x).\nonumber \] Comparing this with Equation \ref{eq:2.6.15} shows that \(\psi'(x)= 2xe^{-x^2}\); therefore, we can let \(\psi(x)=-e^{-x^2}\) in Equation \ref{eq:2.6.17} and conclude that \[e^{-x^2}\left(y^2(x^2y+2)-1\right)=c\nonumber \] is an implicit solution of Equation \ref{eq:2.6.14}. It is also an implicit solution of Equation \ref{eq:2.6.13}.
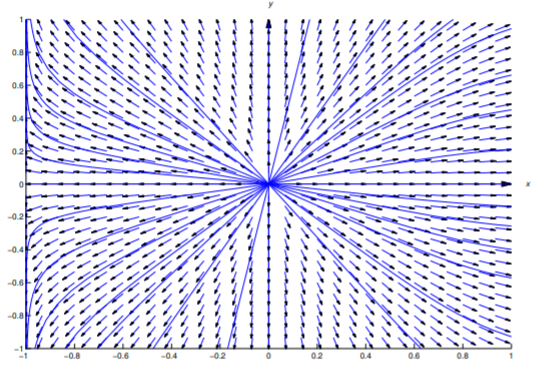
Figure 2.6.1 shows a direction field and some integral curves for Equation \ref{eq:2.6.13}
Find an integrating factor for
\[\label{eq:2.6.30} 2xy^{3}dx+(3x^{2}y^{2}+x^{2}y^{3}+1)dy=0\]
and solve the equation.
Solution
In Equation \ref{eq:2.6.30},
\[M=2xy^{3},\quad N=3x^{2}y^{2}+x^{2}y^{3}+1,\nonumber \]
and
\[M_{y}-N_{x}=6x^{2}-(6xy^{2}+2xy^{3})=-2xy^{3},\nonumber \]
so Equation \ref{eq:2.6.30} isn't exact. Moreover,
\[\frac{M_y-N_x}{N}=-\frac{2xy^3}{3x^2y^2+x^2y^2+1}\nonumber \]
is not independent of \(y\), so Theorem 2.6.1(a) does not apply. However, Theorem 2.6.1(b) does apply, since
\[\frac{N_x-M_y}{M}=\frac{2xy^3}{2xy^3}=1\nonumber \]
is not independent of \(x\), so we can take \(q(y)=1\). Since
\[\int q(y)dy=\int dy=y,\nonumber \]
\(\mu (y)=e^{y}\) is an integrating factor. Multiplying Equation \ref{eq:2.6.30} by \(\mu\) yields the exact equation.
\[\label{eq:2.6.36} 2xy^{3}e^{y}dx+(3x^{2}y^{2}+x^{2}y^{3}+1)e^{y}dy=0.\]
To solve this equation, we must find a function \(F\) such that
\[\label{eq:2.6.37} F_x (x,y)=2xy^{3}e^{y}\]
and
\[\label{eq:2.6.38} F_{y}(x,y)=(3x^{2}y^{2}+x^{2}y^{3}+1)e^{y}.\]
Integrating Equation \ref{eq:2.6.37} with respect to \(x\) yields
\[\label{eq:2.6.39} F (x,y)=x^{2} y^{3} e^{y} + \phi (y)\]
Differentiating this with respect to \(y\) yields
\[F_{y}= (3x^{2} y^{2} + x^{2} y^{3}) e^{y} + \phi ' (y)\nonumber \]
and comparing this with Equation \ref{eq:2.6.38} shows that φ 0 (y) = e y . Therefore we set φ(y) = e y in Equation \ref{eq:2.6.39} and conclude that
\[(x^{2}y^{3}+1)e^{y}=c\nonumber \]
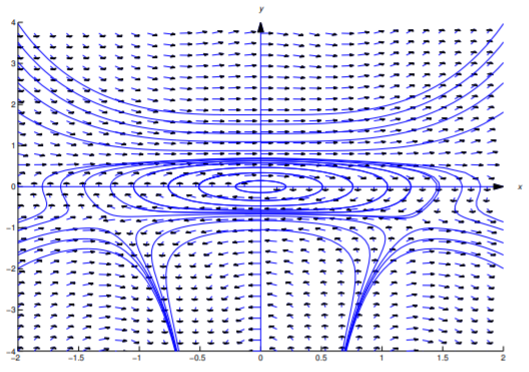
is an implicit solution of \ref{eq:2.6.36}. It is also an implicit solution of \ref{eq:2.6.30}. Figure 2.6.2 shows a direction field and some integral curves for \ref{eq:2.6.30}.
Theorem 2.6.1 does not apply in the next example, but the more general argument that led to Theorem 2.6.1 provides an integrating factor.
Find an integrating factor for
\[\label{eq:2.6.42} (3xy+6y^{2})dx+(2x^{2} +9xy)dy=0\]
and solve the equation.
Solution
In Equation \ref{eq:2.6.42}
\[M=3xy+6y^2, \quad N=2x^2+9xy,\nonumber \]
and
\[M_y -N_x =(3x+12y)-(4x+9y)=-x+3y.\nonumber \]
Therefore
\[\frac{M_y - N_x}{M}=\frac{-x+3y}{3xy+6y^2}\quad\text{and}\quad\frac{N_x - M_y}{N}=\frac{x-3y}{2x^2 +9xy}\nonumber \]
so Theorem 2.6.1 does not apply. Following the more general argument that led to Theorem 2.6.1 , we look for functions \(p = p(x)\) and \(q = q(y)\) such that
\[M_y - N_x = p(x)N-q(y)M;\nonumber \]
that is,
\[-x+3y=p(x)(2x^2+9xy)-q(y)(3xy+6y^2).\nonumber \]
Since the left side contains only first degree terms in \(x\) and \(y\), we rewrite this equation as
\[xp(x)(2x+9y)-yq(y)(3x+6y)=-x+3y.\nonumber \]
This will be an identity if
\[\label{eq:2.6.49} xp(x)=A\quad\text{and}yq(y)=B,\]
where \(A\) and \(B\) are constants such that
\[-x+3y=A(2x+9y)-B(3x+6y),\nonumber \]
or, equivalently,
\[-x+3y=(2A-3B)x+(9A-6B)y.\nonumber \]
Equating the coefficients of x and y on both sides shows that the last equation holds for all \((x, y)\) if
\[\begin{aligned} 2A-3B &=-1 \\ 9A-6B &=3 \end{aligned}\nonumber \]
which has the solution A = 1, B = 1. Therefore Equation \ref{eq:2.6.49} implies that
\[p(x)=\frac{1}{x}\quad\text{and}\quad q(y)=\frac{1}{y}.\nonumber \]
Since
\[\int p(x)dx=\ln |x|\quad\text{and}\quad\int q(y)dy=\ln |y|,\nonumber \]
we can let \(P(x) = x\) and \(Q(y) = y\); hence, \(µ(x, y) = xy\) is an integrating factor. Multiplying Equation \ref{eq:2.6.42} by \(µ\) yields the exact equation
\[(3x^{2}y^{2}+6xy^{3})dx + (2x^{3}y+9x^{2}y^{2})dy=0.\nonumber \]
We leave it to you to use the method of Section 2.5 to show that this equation has the implicit solution
\[\label{eq:2.6.55} x^{3}y^{2}+3x^{2}y^{3}=c.\]
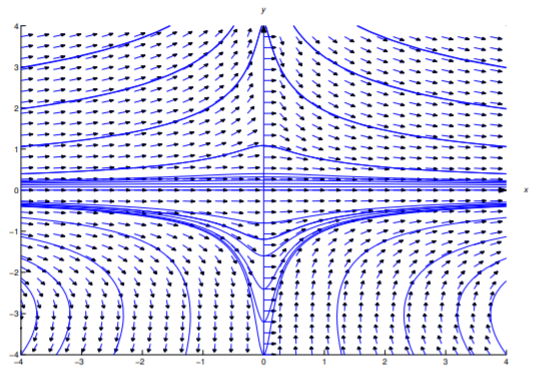
This is also an implicit solution of Equation \ref{eq:2.6.42}. Since x ≡ 0 and y ≡ 0 satisfy Equation \ref{eq:2.6.55}, you should check to see that x ≡ 0 and y ≡ 0 are also solutions of Equation \ref{eq:2.6.42}. (Why is it necesary to check this?) Figure 2.6.3 shows a direction field and integral curves for Equation \ref{eq:2.6.42}. See Exercise 2.6.28 for a general discussion of equations like Equation \ref{eq:2.6.42}.
The separable equation
\[\label{eq:2.6.56} -ydx+(x+x^{6})dy=0\]
can be converted to the exact equation
\[\label{eq:2.6.57} -\frac{dx}{x+x^{6}}+\frac{dy}{y}=0\]
by multiplying through by the integrating factor
\[\mu (x,y)=\frac{1}{y(x+x^{6})}.\nonumber \]
However, to solve Equation \ref{eq:2.6.57} by the method of Section 2.5 we would have to evaluate the nasty integral
\[\int\frac{dx}{x+x^{6}}.\nonumber \]
Instead, we solve Equation \ref{eq:2.6.56} explicitly for \(y\) by finding an integrating factor of the form \(µ(x, y) = x^{a}y^{b}\).
Solution
In Equation \ref{eq:2.6.56}
\[M=-y,\ N=x+x^6,\nonumber \]
and
\[M_y-N_x=-1-(1+6x^5)=-2-6x^5.\nonumber \]
We look for functions \(p=p(x)\) and \(q=q(y)\) such that
\[M_y-N_x=p(x)N-q(y)M;\nonumber \]
that is,
\[\label{eq:2.6.28} -2-6x^5=p(x)(x+x^6)+q(y)y.\]
The right side will contain the term \(-6x^5\) if \(p(x)=-6/x\). Then Equation \ref{eq:2.6.28} becomes
\[-2-6x^5=-6-6x^5+q(y)y,\nonumber \]
so \(q(y)=4/y\). Since
\[\int p(x)\,dx=-\int{6\over x}\,dx=-6\ln|x|=\ln{1\over x^6},\nonumber \]
and
\[\int q(y)\,dy=\int{4\over y}\,dy=4\ln |y|=\ln{y^4},\nonumber \]
we can take \(P(x)=x^{-6}\) and \(Q(y)=y^4\), which yields the integrating factor \(\mu(x,y)=x^{-6}y^4\). Multiplying Equation \ref{eq:2.6.56} by \(\mu\) yields the exact equation
\[-{y^5\over x^6}\,dx+\left({y^4\over x^5}+y^4\right) \,dy=0.\nonumber \]
We leave it to you to use the method of the Section 2.5 to show that this equation has the implicit solution
\[\left({y\over x}\right)^5+y^5=k.\nonumber \]
Solving for \(y\) yields
\[y=k^{1/5}x(1+x^5)^{-1/5},\nonumber \]
which we rewrite as
\[y=cx(1+x^5)^{-1/5}\nonumber \]
by renaming the arbitrary constant. This is also a solution of Equation \ref{eq:2.6.56}.
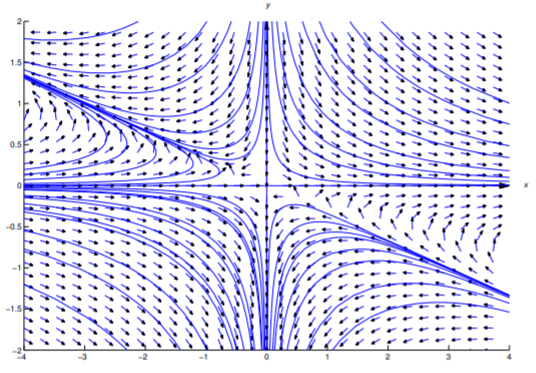
Figure 2.6.4 shows a direction field and some integral curves for Equation \ref{eq:2.6.56}.