6.4E: Motion Under a Central Force (Exercises)
- Page ID
- 18280
Q6.4.1
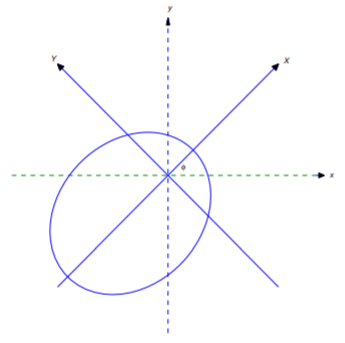
1. Find the equation of the curve
\[r={\rho\over 1+e\cos(\theta-\phi)} \tag{A}\]
in terms of \((X,Y)=\left(r\cos(\theta-\phi),r\sin(\theta-\phi)\right)\), which are rectangular coordinates with respect to the axes shown in Figure 6.4E.1 . Use your results to verify that (A) is the equation of an ellipse if \(0<e<1\), a parabola if \(e=1\), or a hyperbola if \(e>1\). If \(e<1\), leave your answer in the form
\[{(X-X_0)^2\over a^2}+{(Y-Y_0)^2\over b^2}=1,\]
and show that the area of the ellipse is
\[A={\pi\rho^2\over(1-e^2)^{3/2}}.\]
Then use Theorem 6.4.1 to show that the time required for the object to traverse the entire orbit is
\[T={2\pi\rho^2\over h(1-e^2)^{3/2}}.\]
(This is Kepler’s third law; \(T\) is called the period of the orbit.)
2. Suppose an object with mass \(m\) moves in the \(xy\)-plane under the central force
\[{\bf F}(r,\theta)=-{mk\over r^2}(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}),\]
where \(k\) is a positive constant. As we shown, the orbit of the object is given by
\[r={\rho\over 1+e\cos(\theta-\phi)}.\]
Determine \(\rho\), \(e\), and \(\phi\) in terms of the initial conditions
\[r(0)=r_0,\quad r'(0)=r_0', \quad\text{and}\quad \theta(0)=\theta_0,\quad \theta'(0)=\theta_0'.\]
Assume that the initial position and velocity vectors are not collinear.
3. Suppose we wish to put a satellite with mass \(m\) into an elliptical orbit around Earth. Assume that the only force acting on the object is Earth’s gravity, given by
\[{\bf F}(r,\theta)=-mg\left(R^2\over r^2\right)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}),\]
where \(R\) is Earth’s radius, \(g\) is the acceleration due to gravity at Earth’s surface, and \(r\) and \(\theta\) are polar coordinates in the plane of the orbit, with the origin at Earth’s center.
- Find the eccentricity required to make the aphelion and perihelion distances equal to \(R\gamma_1\) and \(R\gamma_2\), respectively, where \(1<\gamma_1<\gamma_2\).
- Find the initial conditions \[r(0)=r_0,\quad r'(0)=r_0',\quad \text{and} \quad \theta(0)=\theta_0,\quad \theta'(0)=\theta_0'\] required to make the initial point the perigee, and the motion along the orbit in the direction of increasing \(\theta\). HINT: Use the results of Exercise 6.4.2
4. An object with mass \(m\) moves in a spiral orbit \(r=c\theta^2\) under a central force
\[{\bf F}(r,\theta)=f(r)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}).\]
Find \(f\).
5. An object with mass \(m\) moves in the orbit \(r=r_0e^{\gamma\theta}\) under a central force
\[{\bf F}(r,\theta)=f(r)(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}).\]
Find \(f\).
6. Suppose an object with mass \(m\) moves under the central force
\[{\bf F}(r,\theta)=-{mk\over r^3}(\cos\theta\,{\bf i}+\sin\theta\,{\bf j}),\]
with
\[r(0)=r_0,\quad r'(0)=r_0', \quad\text{and}\quad \theta(0)=\theta_0,\quad \theta'(0)=\theta_0',\]
where \(h=r_0^2\theta_0'\ne0\).
- Set up a second order initial value problem for \(u=1/r\) as a function of \(\theta\).
- Determine \(r=r(\theta)\) if (i) \(h^2<k\); (ii) \(h^2=k\); (iii) \(h^2>k\).


