6.3: Maximum Principle
- Page ID
- 2158
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let \(\Omega\subset \mathbb{R}^n\) be a bounded domain. Set
\begin{eqnarray*}
D_T&=&\Omega\times(0,T),\ \ T>0,\\
S_T&=&\{(x,t):\ (x,t)\in\Omega\times\{0\}\ \mbox{or}\ (x,t)\in\partial\Omega\times[0,T]\},
\end{eqnarray*}
see Figure 6.3.1.
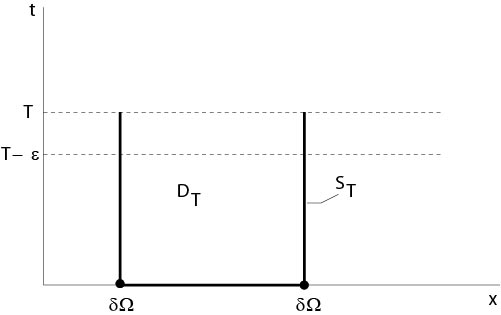
Figure 6.3.1: Notations to the maximum principle
Theorem 6.2
Assume \(u\in C(\overline{D_T})\), that \(u_t\), \(u_{x_ix_k}\) exist and are continuous in \(D_T\), and
$$u_t-\triangle u\le 0\ \ \mbox{in}\ D_T.\]
Then
$$\max_{\overline{D_T}} u(x,t)=\max_{S_T} u.\]
Proof
Assume initially \(u_t-\triangle u<0\) in \(D_T\). Let \(\varepsilon>0\) be small and \(0<\varepsilon<T\). Since \(u\in C(\overline{D_{T-\varepsilon}})\), there is an \((x_0,t_0) \in \overline{D_{T-\varepsilon}}\) such that
$$u(x_0,t_0)=\max_{\overline{D_{T-\varepsilon}}} u(x,t).\]
Case (i)
Let \((x_0,t_0)\in D_{T-\varepsilon}\). Hence, since \(D_{T-\varepsilon}\) is open,
\(u_t(x_0,t_0)=0\), \(u_{x_l}(x_0,t_0)=0\), \(l=1,\ldots,n\) and
$$\sum_{l,k=1}^n u_{x_lx_k}(x_0,t_0)\zeta_l\zeta_k\le0\ \ \mbox{for all}\ \zeta\in\mathbb{R}^n.\]
The previous inequality implies that \(u_{x_kx_k}(x_0,t_0)\le0\) for each \(k\). Thus we arrived at a contradiction to \(u_t-\triangle u<0\) in \(D_T\).
Case (ii)
Assume \((x_0,t_0)\in\Omega\times\{T-\varepsilon\}\). Then it follows as above \(\triangle u\le 0\) in \((x_0,t_0)\), and from \(u(x_0,t_0)\ge u(x_0,t)\), \(t\le t_0\), one concludes that \(u_t(x_0,t_0)\ge0\). We arrived at a contradiction to \(u_t-\triangle u<0\) in \(D_T\) again.
Summarizing, we have shown that
$$\max_{\overline{D_{T-\varepsilon}}} u(x,t)=\max_{T-\varepsilon} u(x,t).\]
Thus there is an \((x_\varepsilon,t_\varepsilon)\in S_{T-\varepsilon}\) such that
$$u(x_\varepsilon,t_\varepsilon)=\max_{\overline{D_{T-\varepsilon}}} u(x,t).\]
Since \(u\) is continuous on \(\overline{D}_T\), we have
$$\lim_{\varepsilon\to 0}\max_{\overline{D_{T-\varepsilon}}} u(x,t)=\max_{\overline{D_T}} u(x,t).\]
It follows that there is \((\overline{x},\overline{t})\in S_T\) such that
$$u(\overline{x},\overline{t})=\max_{\overline{D_T}} u(x,t)\]
since \(S_{T-\varepsilon}\subset S_T\) and \(S_T\) is compact. Thus, theorem is shown under the assumption \(u_t-\triangle u<0\) in \(D_T\). Now assume \(u_t-\triangle u\le 0\) in \(D_T\). Set
$$v(x,t):=u(x,t)-kt,\]
where \(k\) is a positive constant. Then
$$v_t-\triangle v=u_t-\triangle u-k<0.\]
From above we have
\begin{eqnarray*}
\max_{\overline{D_T}} u(x,t)&=&\max_{\overline{D_T}} (v(x,t)+kt)\\
&\le&\max_{\overline{D_T}} v(x,t)+kT\\
&=&\max_{S_T} v(x,t)+kT\\
&\le&\max_{S_T}u(x,t)+kT,
\end{eqnarray*}
Letting \(k\to 0\), we obtain
$$\max_{\overline{D_T}} u(x,t)\le\max_{S_T} u(x,t).\]
Since \(S_T\subset\overline{D_T}\), the theorem is shown.
\(\Box\)
If we replace in the above theorem the bounded domain \(\Omega\) by \(\mathbb{R}^n\), then the result remains true provided we assume an {\it additional} growth assumption for \(u\). More precisely, we have the following result which is a corollary of the previous theorem. Set for a fixed \(T\), \(0<T<\infty\),
$$D_T=\{ (x,t):\ x\in\mathbb{R}^n,\ 0<t<T\}.\]
Proposition 6.2
Assume \(u\in C(\overline{D_T})\), that \(u_t\), \(u_{x_ix_k}\) exist and are continuous in \(D_T\),
$$u_t-\triangle u\le 0\ \ \mbox{in}\ D_T,\]
and additionally that \(u\) satisfies the growth condition
$$u(x,t)\le Me^{a|x|^2},\]
where \(M\) and \(a\) are positive constants.
Then
$$\max_{\overline{D_T}} u(x,t)=\max_{S_T} u.\]
It follows immediately the
Corollary
The initial value problem \(u_t-\triangle u=0\) in \(D_T\), \(u(x,0)=f(x)\), \(x\in\mathbb{R}^n\), has a unique solution in the class defined by \(u\in C(\overline{D_T})\), \(u_t\), \(u_{x_ix_k}\) exist and are continuous in \(D_T\) and \(|u(x,t)|\le Me^{a|x|^2}\).
Proof of Proposition 6.2.
See [10], pp. 217. We can assume that \(4aT<1\), since the finite interval can be divided into finite many intervals of equal length \(\tau\) with
\(4a\tau<1\). Then we conclude successively for \(k\) that
$$u(x,t)\le\sup_{y\in\mathbb{R}^n}u(y,k\tau)\le\sup_{y\in\mathbb{R}^n}u(y,0)\]
for \(k\tau\le t\le (k+1)\tau\), \(k=0,\ldots, N-1\), where \(N=T/\tau\).
There is an \(\epsilon>0\) such that \(4a(T+\epsilon)<1\). Consider the comparison function
\begin{eqnarray*}
v_\mu(x,t):&=&u(x,t)-\mu\left(4\pi(T+\epsilon-t)\right)^{-n/2}e^{|x-y|^2/(4(T+\epsilon-t))}\\
&=&u(x,t)-\mu K(ix,iy,T+\epsilon-t)
\end{eqnarray*}
for fixed \(y\in\mathbb{R}^n\) and for a constant \(\mu>0\). Since the heat kernel \(K(ix,iy,t)\) satisfies \(K_t=\triangle K_x\), we obtain
$$\frac{\partial}{\partial t}v_\mu-\triangle v_\mu=u_t-\triangle u\le0.\]
Set for a constant \(\rho>0\)
$$D_{T,\rho}=\{(x,t):\ |x-y|<\rho,\ 0<t<T\}.\]
Then we obtain from Theorem 6.2 that
$$v_\mu(y,t)\le\max_{S_{T,\rho}}v_\mu,\]
where \(S_{T,\rho}\equiv S_T\) of Theorem 6.2 with \(\Omega=B_\rho(y)\), see Figure 6.3.1.
On the bottom of \(S_{T,\rho}\) we have, since \(\mu K>0\),
$$v_\mu(x,0)\le u(x,0)\le\sup_{z\in\mathbb{R}^n}f(z).\]
On the cylinder part \(|x-y|=\rho\), \(0\le t\le T\), of \(S_{T,\rho}\) it is
\begin{eqnarray*}
v_\mu(x,t)&\le&Me^{a|x|^2}-\mu\left(4\pi(T+\epsilon-t)\right)^{-n/2}e^{\rho^2/(4(T+\epsilon-t))}\\
&\le&Me^{a(|y|+\rho)^2}-\mu\left(4\pi(T+\epsilon)\right)^{-n/2}e^{\rho^2/(4(T+\epsilon))}\\
&\le&\sup_{z\in\mathbb{R}^n}f(z)
\end{eqnarray*}
for all \(\rho>\rho_0(\mu)\), \(\rho_0\) sufficiently large. We recall that \(4a(T+\epsilon)<1\).
Summarizing, we have
$$\max_{S_{T,\rho}}v_\mu(x,t)\le\sup_{z\in\mathbb{R}^n}f(z)\]
if \(\rho>\rho_0(\mu)\). Thus
$$v_\mu(y,t)\le\max_{S_{T,\rho}}v_\mu(x,t)\le\sup_{z\in\mathbb{R}^n}f(z)\]
if \(\rho>\rho_0(\mu)\).
Since
$$v_\mu(y,t)=u(y,t)-\mu\left(4\pi(T+\epsilon-t)\right)^{-n/2}\]
it follows
$$u(y,t)-\mu\left(4\pi(T+\epsilon-t)\right)^{-n/2}\le\sup_{z\in\mathbb{R}^n}f(z).\]
Letting \(\mu\to0\), we obtain the assertion of the proposition.
\(\Box\)
The above maximum principle of Theorem 6.2 holds for a large class of parabolic differential operators, even for degenerate equations.
Set
$$Lu=\sum_{i,j=1}^na^{ij}(x,t)u_{x_ix_j},\]
where \(a^{ij}\in C(D_T)\) are real, \(a^{ij}=a^{ji}\), and the matrix \((a^{ij})\) is non-negative, that is,
$$\sum_{i,j=1}^na^{ij}(x,t)\zeta_i\zeta_j\ge 0\ \ \mbox{for all}\ \zeta\in\mathbb{R}^n,\]
and \((x,t)\in D_T\).
Theorem 6.3
Assume \(u\in C(\overline{D_T})\), that \(u_t\), \(u_{x_ix_k}\) exist and are continuous in \(D_T\), and
$$u_t-L u\le 0\ \ \mbox{in}\ D_T.\]
Then
$$\max_{\overline{D_T}} u(x,t)=\max_{S_T} u.\]
Proof
(i) One proof is a consequence of the following lemma: let \(A\), \(B\) real, symmetric and non-negative matrices. Non-negative means that all eigenvalues are non-negative. Then trace~\((AB)\equiv\sum_{i,j=1}^na^{ij}b_{ij}\ge0\), see an exercise.
(ii) Another proof is more directly: let \(U=(z_1,\ldots,z_n)\), where \(z_l\) is an orthonormal system of eigenvectors to the eigenvalues \(\lambda_l\) of the matrix \(A=(a^{i,j}(x_0,t_0))\). Set \(\zeta=U\eta\), \(x=U^T(x-x_0)y\) and \(v(y)=u(x_0+Uy,t_0)\), then
\begin{eqnarray*}
0&\le&\sum_{i,j=1}^na^{ij}(x_0,t_0)\zeta_i\zeta_j=\sum_{i=1}^n\lambda_i\eta_i^2\\
0&\ge&\sum_{i,j=1}^n u_{x_ix_j}\zeta_i\zeta_j=\sum_{i=1}^n v_{y_iy_i}\eta_i^2.
\end{eqnarray*}
It follows \(\lambda_i\ge0\) and \(v_{y_iy_i}\le0\) for all \(i\).
Consequently
$$\sum_{i,j=1}^na^{ij}(x_0,t_0)u_{x_ix_j}(x_0,t_0)=\sum_{i=1}^n\lambda_iv_{y_iy_i}\le0.\]
\(\Box\)
Contributors and Attributions
Integrated by Justin Marshall.


