Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

7.2: Spherical Coordinates

  1. Last updated
  2. Save as PDF
  • Page ID
    8340

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

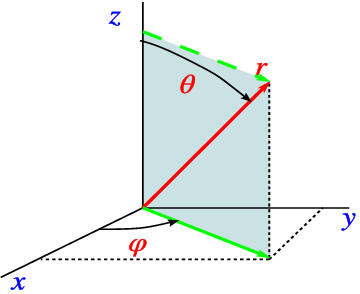
    Spherical coordinates are defined from Cartesian coordinates as

    \[\begin{aligned} r &= \sqrt{x^2+y^2+z^2} \\[4pt] \phi &= \arctan(y/x) \\[4pt] \theta &=\arctan\left(\frac{\sqrt{x^2+y^2}}{z}\right)\end{aligned}\]

    or alternatively

    \[\begin{aligned} x &= r \cos\phi\sin\theta,\\[4pt] y &= r \sin\phi\sin\theta \\[4pt] z &=r \cos\theta\end{aligned}\]

    as indicated schematically in Fig. \(\PageIndex{1}\).

    spherical.png
    Figure \(\PageIndex{1}\): Spherical coordinates

    Using the chain rule we find

    \[\begin{aligned} \frac{\partial}{\partial x}{~} &= \frac{\partial r}{\partial x}\frac{\partial}{\partial r}{~} + \frac{\partial \phi}{\partial x}\frac{\partial}{\partial \phi}{~} + \frac{\partial \theta}{\partial x}\frac{\partial}{\partial \theta}{~}\nonumber\\[4pt] &= \frac{x}{r} \frac{\partial}{\partial r}{~}-\frac{y}{x^2+y^2}\frac{\partial}{\partial \phi}{~} +\frac{xz}{r^2\sqrt{x^2+y^2}}\frac{\partial}{\partial \theta}{~} \nonumber\\[4pt] &= \sin\theta\cos\phi\frac{\partial}{\partial r}{~}-\frac{\sin\phi}{r\sin\theta} \frac{\partial}{\partial \phi}{~} +\frac{\cos\phi\cos\theta}{r} \frac{\partial}{\partial \theta}{~},\\[4pt] \frac{\partial}{\partial y}{~} &= \frac{\partial r}{\partial y}\frac{\partial}{\partial r}{~}+\frac{\partial \phi}{\partial y}\frac{\partial}{\partial \phi}{~}+\frac{\partial \theta}{\partial y}\frac{\partial}{\partial \theta}{~}\nonumber\\[4pt] &= \frac{y}{r} \frac{\partial}{\partial r}{~}+\frac{x}{x^2+y^2}\frac{\partial}{\partial \phi}{~} +\frac{yz}{r^2\sqrt{x^2+y^2}}\frac{\partial}{\partial \theta}{~} \nonumber\\[4pt] &= \sin\theta\sin\phi\frac{\partial}{\partial r}{~}+\frac{\cos\phi}{r\sin\theta} \frac{\partial}{\partial \phi}{~} +\frac{\sin\phi\cos\theta}{r} \frac{\partial}{\partial \theta}{~},\\[4pt] \frac{\partial}{\partial z}{~} &= \frac{\partial r}{\partial z}\frac{\partial}{\partial r}{~}+\frac{\partial \phi}{\partial z}\frac{\partial}{\partial \phi}{~}+\frac{\partial \theta}{\partial z}\frac{\partial }{\partial \theta}{~}\nonumber\\[4pt] &= \frac{z}{r} \frac{\partial }{\partial r}{~} -\frac{\sqrt{x^2+y^2}}{r^2}\frac{\partial }{\partial \theta}{~} \nonumber\\[4pt] &= \sin\theta\sin\phi\frac{\partial }{\partial r}{~}-\frac{\sin\theta}{r} \frac{\partial }{\partial \theta}{~}.\\[4pt]\end{aligned}\]

    once again we can write \({\nabla}\) in terms of these coordinates.

    \[\begin{aligned} {\nabla} &=& \hat{e}_r \frac{\partial}{\partial r}{~}+\hat{e}_\phi \frac{1}{r\sin\theta}\frac{\partial}{\partial \phi}{~} + \hat{e}_\theta \frac{1}{r}\frac{\partial}{\partial \theta}{~}\end{aligned}\] where the unit vectors \[\begin{aligned} \hat{e}_r &=& (\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta), \nonumber\\[4pt] \hat{e}_\phi &=& (-\sin\phi,\cos\phi,0), \nonumber\\[4pt] \hat{e}_\theta &=& (\cos\phi\cos\theta,\sin\phi\cos\theta,-\sin\theta).\end{aligned}\]

    are an orthonormal set. We say that spherical coordinates are orthogonal.

    We can use this to evaluate \(\Delta={\nabla}^2\),

    \[\Delta = \frac{1}{r^2}\frac{\partial}{\partial r}{~}\left(r^2 \frac{\partial}{\partial r}{~}\right) +\frac{1}{r^2} \frac{1}{\sin\theta} \frac{\partial}{\partial \theta}{~} \left( \sin\theta\frac{\partial}{\partial \theta}{~} \right) + \frac{1}{r^2}\frac{\partial^2}{\partial \phi^2}{~}\]

    Finally, for integration over these variables we need to know the volume of the small cuboid contained between \(r\) and \(r+\delta r\), \(\theta\) and \(\theta + \delta\theta\) and \(\phi\) and \(\phi+\delta\phi\).

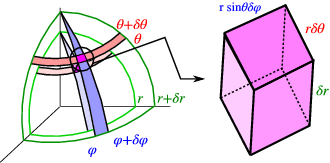
    spherical2.png
    Figure \(\PageIndex{2}\): Integration in spherical coordinates

    The length of the sides due to each of these changes is \(\delta r\), \(r \delta \theta\) and \(r \sin \theta \delta \theta\), respectively (these are the Jacobians for the conversion of Cartesian coordinates to polar and spherical coordinates, respectively). We thus conclude that

    \[\int_V f(x,y,z) dx dy dz = \int_V f(r,\theta,\phi) r^2\sin\theta \,dr \,d\theta \,d\phi.\]

    Contributors