1.14: Complex Numbers
- Page ID
- 90397
View tutorial on YouTube: Complex Numbers
View tutorial on YouTube: Complex Exponential Function
We define the imaginary number \(i\) to be one of the two numbers that satisfies the rule \((i)^2 = −1\), the other number being \(−i\). Formally, we write \(i =\sqrt{−1}\). A complex number \(z\) is written as \[z=x+iy,\nonumber\] where \(x\) and \(y\) are real numbers. We call \(x\) the real part of \(z\) and \(y\) the imaginary part and write \[x=\text{Re }z,\quad y=\text{Im }z.\nonumber\]
Two complex numbers are equal if and only if their real and imaginary parts are equal.
The complex conjugate of \(z = x + iy\), denoted as \(\overline{z}\), is defined as \[\overline{z}=x-iy.\nonumber\]
Using \(z\) and \(\overline{z}\), we have \[\label{eq:1}\text{Re }z=\frac{1}{2}(z+\overline{z}),\quad\text{Im }z=\frac{1}{2i}(z-\overline{z}).\]
Furthermore, \[\begin{aligned}z\overline{z}&=(x+iy)(x-iy) \\ &=x^2-i^2y^2 \\ &=x^2+y^2;\end{aligned}\] and we define the absolute value of \(z\), also called the modulus of \(z\), by \[\begin{aligned} |z|&=(z\overline{z})^{1/2} \\ &=\sqrt{x^2+y^2}.\end{aligned}\]
We can add, subtract, multiply and divide complex numbers to get new complex numbers. With \(z = x + iy\) and \(w = s + it\), and \(x,\) \(y,\) \(s,\) \(t\) real numbers, we have \[ z + w = (x + s) + i(y + t);\quad z − w = (x − s) + i(y − t);\nonumber\]
\[\begin{aligned} zw&=(x+iy)(s+it) \\ &=(xs-yt)+i(xt+ys); \\ & \\ \frac{z}{w}&=\frac{z\overline{w}}{w\overline{w}} \\ &=\frac{(x+iy)(s-it)}{s^2+t^2} \\ &=\frac{(xs+yt)}{s^2+t^2}+i\frac{(ys-xt)}{s^2+t^2}.\end{aligned}\]
Furthermore, \[\begin{aligned} |zw|&=\sqrt{(xs-yt)^2+(xt+ys)^2} \\ &=\sqrt{(x^2+y^2)(s^2+t^2)} \\ &=|z||w|;\end{aligned}\] and \[\begin{aligned}\overline{zw}&=(xs-yt)-i(xt+ys) \\ &=(x-iy)(s-it) \\ &=\overline{z}\overline{w}.\end{aligned}\]
Similarly \[\left|\frac{z}{w}\right| =\frac{|z|}{|w|},\quad\overline{\left(\frac{z}{w}\right)}=\frac{\overline{z}}{\overline{w}}.\nonumber\]
Also, \(\overline{z + w} = \overline{z} + \overline{w}\). However, \(|z + w| ≤ |z| + |w|\), a theorem known as the triangle inequality.
It is especially interesting and useful to consider the exponential function of an imaginary argument. Using the Taylor series expansion of an exponential function, we have \[\begin{aligned}e^{i\theta}&=1+(i\theta )+\frac{(i\theta )^2}{2!}+\frac{(i\theta )^3}{3!}+\frac{(i\theta )^4}{4!}+\frac{(i\theta )^5}{5!}\cdots \\ &=\left(1-\frac{\theta^2}{2!}+\frac{\theta^4}{4!}-\cdots\right)+i\left(\theta -\frac{\theta^3}{3!}+\frac{\theta^5}{5!}+\cdots\right) \\ &=\cos\theta +i\sin\theta.\end{aligned}\]
Since we have determined that \[\label{eq:2}\cos\theta=\text{Re }e^{i\theta },\quad\sin\theta =\text{Im }e^{i\theta },\] we also have using \(\eqref{eq:1}\) and \(\eqref{eq:2}\), the frequently used expressions \[\cos\theta =\frac{e^{i\theta}+e^{-i\theta }}{2},\quad\sin\theta=\frac{e^{i\theta}-e^{-i\theta}}{2i}.\nonumber\]
The much celebrated Euler’s identity derives from \(e^{iθ} = \cos θ + i \sin θ\) by setting \(θ = π\), and using \(\cos π = −1\) and \(\sin π = 0\):
\[e^{i\pi}+1=0,\nonumber\] and this identity links the five fundamental numbers—\(0,\: 1,\: i,\: e\) and \(π\)—using three basic mathematical operations—addition, multiplication and exponentiation—only once.
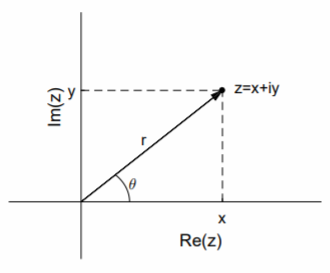
The complex number \(z\) can be represented in the complex plane with \(\text{Re }z\) as the \(x\)-axis and \(\text{Im }z\) as the \(y\)-axis (see Figure \(\PageIndex{1}\)). This leads to the polar representation of \(z = x + iy\):
\[z=re^{i\theta},\nonumber\] where \(r = |z|\) and \(\tan θ = y/x\). We define \(\text{arg }z = θ\). Note that \(θ\) is not unique, though it is conventional to choose the value such that \(−π < θ ≤ π\), and \(θ = 0\) when \(r = 0\).
The polar form of a complex number can be useful when multiplying numbers. For example, if \(z_1=r_1e^{i\theta _1}\) and \(z_2=r_2e^{i\theta _2}\), then \(z_1z_2 = r_1r_2e^{i(θ_1+θ_2)}\). In particular, if \(r_2 = 1\), then multiplication of \(z_1\) by \(z_2\) spins the representation of \(z_1\) in the complex plane an angle \(θ_2\) counterclockwise.
Useful trigonometric relations can be derived using \(e^{iθ}\) and properties of the exponential function. The addition law can be derived from \[e^{i(x+y)}=e^{ix}e^{iy}.\nonumber\]
We have \[\begin{aligned} \cos(x + y) + i \sin(x + y) &= (\cos x + i \sin x)(\cos y + i \sin y) \\ &= (\cos x \cos y − \sin x \sin y) + i(\sin x \cos y + \cos x \sin y);\end{aligned}\] yielding \[ \cos(x + y) = \cos x \cos y − \sin x \sin y,\quad \sin(x + y) = \sin x \cos y + \cos x \sin y.\nonumber\]
De Moivre’s Theorem derives from \(e^{inθ} = (e^{iθ})^n\), yielding the identity \[\cos(nθ) + i \sin(nθ) = (\cos θ + i \sin θ)^n.\nonumber\]
For example, if \(n=2\), we derive \[\begin{aligned} \cos 2\theta +i\sin 2\theta &=(\cos\theta +i\sin\theta)^2 \\ &=(\cos^2\theta -\sin^2\theta)+2i\cos\theta\sin\theta.\end{aligned}\]
Therefore, \[\cos 2θ = \cos^2 θ − \sin^2 θ,\quad \sin 2θ = 2 \cos θ \sin θ.\nonumber\]
Write \(\sqrt{i}\) as a standard complex number
Solution
To solve this example, we first need to define what is meant by the square root of a complex number. The meaning of \(\sqrt{z}\) is the complex number whose square is \(z\). There will always be two such numbers, because \((\sqrt{z})^2 = (−\sqrt{z})^2 = z\). One can not define the positive square root because complex numbers are not defined as positive or negative.
We will show two methods to solve this problem. The first most straightforward method writes \[\sqrt{i}=x+iy.\nonumber\]
Squaring both sides, we obtain \[i=x^2-y^2+2xyi;\nonumber\] and equating the real and imaginary parts of this equation yields the two real equations \[x^2-y^2=0,\quad 2xy=1.\nonumber\]
The first equation yields \(y = ±x\). With \(y = x\), the second equation yields \(2x^2 = 1\) with two solutions \(x = ±\sqrt{2}/2\). With \(y = −x\), the second equation yields \(−2x^2 = 1\), which has no solution for real \(x\). We have therefore found that \[\sqrt{i}=\pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right).\nonumber\]
The second solution method makes use of the polar form of complex numbers. The algebra required for this method is somewhat simpler, especially for finding cube roots, fourth roots, etc. We know that \(i = e^{iπ/2}\), but more generally because of the periodic nature of the polar angle, we can write \[i=e^{i(\frac{\pi}{2}+2\pi k)},\nonumber\] where \(k\) is an integer. We then have \[\sqrt{i}=i^{1/2}=e^{i(\frac{\pi}{4}+\pi k)}=e^{i\pi k}e^{i\pi /4}=\pm e^{i\pi /4},\nonumber\] where we have made use of the usual properties of the exponential function, and \(e^{iπk} = ±1\) for \(k\) even or odd. Converting back to standard form, we have \[\sqrt{i}=\pm (\cos \pi /4+i\sin \pi /4)=\pm\left(\frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2}\right).\nonumber\]
The fundamental theorem of algebra states that every polynomial equation of degree \(n\) has exactly \(n\) complex roots, counted with multiplicity. Two familiar examples would be \(x^2 − 1 = (x + 1)(x − 1) = 0\), with two roots \(x_1 = −1\) and \(x_2 = 1\); and \(x^2 − 2x + 1 = (x − 1)^2 = 0\), with one root \(x_1 = 1\) with multiplicity two.
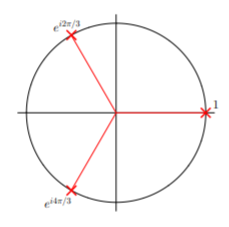
The problem of finding the \(n\)th roots of unity is to solve the polynomial equation \[z^n=1\nonumber\] for the \(n\) complex values of \(z\). We have \(z_1 = 1\) for \(n = 1\); and \(z_1 = 1\), \(z_2 = −1\) for \(n = 2\). Beyond \(n = 2\), some of the roots are complex and here we find the cube roots of unity, that is, the three values of \(z\) that satisfy \(z^3 = 1\). Writing \(1 = e^{i2πk}\), where \(k\) is an integer, we have \[z=(1)^{1/3}=\left(e^{i2\pi k}\right)^{1/3}=e^{i2\pi k/3}=\left\{\begin{array}{l}1; \\ e^{i2\pi /3}; \\ e^{i4\pi /3}.\end{array}\right.\nonumber\]
Using \(\cos (2π/3) = −1/2,\) \(\sin (2π/3) = \sqrt{3}/2,\) \(\cos (4π/3) = −1/2,\) \(\sin (4π/3) = − \sqrt{3}/2,\) the three cube roots of unity are given by \[z_1=1,\quad z_2=-\frac{1}{2}+i\frac{\sqrt{3}}{2},\quad z_3=-\frac{1}{2}-i\frac{\sqrt{3}}{2}.\nonumber\]
These three roots are evenly spaced around the unit circle in the complex plane, as shown in the figure below.