9.4: Fourier Sine and Cosine Series
- Page ID
- 90435
The Fourier series simplifies if \(f(x)\) is an even function such that \(f(−x) = f(x)\), or an odd function such that \(f(−x) = −f(x)\). Use will be made of the following facts. The function \(\cos (n\pi x/L)\) is an even function and \(\sin (n\pi x/L)\) is an odd function. The product of two even functions is an even function. The product of two odd functions is an even function. The product of an even and an odd function is an odd function. And if \(g(x)\) is an even function, then \[\int_{-L}^Lg(x)dx=2\int_0^Lg(x)dx;\nonumber\] and if \(g(x)\) is an odd function, then \[\int_{-L}^Lg(x)dx=0.\nonumber\]
We examine in turn the Fourier series for an even or an odd function. First, if \(f(x)\) is even, then from (9.3.5) and (9.3.6) and our facts about even and odd functions, \[\begin{align}a_n&=\frac{2}{L}\int_0^L f(x)\cos\frac{n\pi x}{L}dx,\label{eq:1} \\ b_n&=0.\nonumber\end{align}\]
The Fourier series for an even function with period \(2L\) is thus given by the Fourier cosine series \[\label{eq:2}f(x)=\frac{a_0}{2}+\sum\limits_{n=1}^\infty a_n\cos\frac{n\pi x}{L},\quad f(x)\text{ even}.\]
Second, if \(f(x)\) is odd, then \[\begin{align} a_n&=0,\nonumber \\ b_n&=\frac{2}{L}\int_0^L f(x)\sin\frac{n\pi x}{L}dx;\label{eq:3}\end{align}\] and the Fourier series for an odd function with period \(2L\) is given by the Fourier sine series \[\label{eq:4}f(x)=\sum\limits_{n=1}^\infty b_n\sin\frac{n\pi x}{L},\quad f(x)\text{ odd.}\]
Examples of Fourier series computed numerically can be obtained using the Java applet found at http://www.falstad.com/fourier. Here, we demonstrate an analytical example.
Determine the Fourier cosine series of the even triangle function represented by Fig. \(\PageIndex{1}\).
Solution
The triangle function depicted in Fig. \(\PageIndex{1}\) is an even function of \(x\) with period \(2\pi\) (i.e., \(L =\pi\)). Its definition on \(0 < x <\pi\) is given by \[f(x)=1-\frac{2x}{\pi}.\nonumber\]
Because \(f(x)\) is even, it can be represented by the Fourier cosine series given by \(\eqref{eq:1}\) and \(\eqref{eq:2}\). The coefficient \(a_0\) is \[\begin{aligned}a_0&=\frac{2}{\pi}\int_0^\pi f(x)dx \\ &=\frac{2}{\pi}\int_0^{\pi}\left(1-\frac{2x}{\pi}\right)dx \\ &=\frac{2}{\pi}\left[x-\frac{x^2}{\pi}\right]_0^\pi \\ &=0.\end{aligned}\]
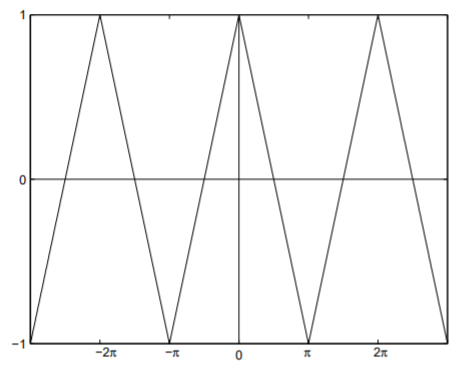
Note that \(a_0/2\) is the average value of \(f(x)\) over one period, and it is obvious from Fig. \(\PageIndex{1}\) that this value is zero. The coefficients for \(n > 0\) are \[\begin{aligned}a_n&=\frac{2}{\pi}\int_0^\pi f(x)\cos (nx)dx \\ &=\frac{2}{\pi}\int_0^\pi \left(1-\frac{2x}{\pi}\right)\cos (nx)dx \\ &=\frac{2}{\pi}\int_0^\pi \cos (nx)dx-\frac{4}{\pi^2}\int_0^\pi x\cos (nx)dx \\ &=\frac{2}{n\pi}\sin (nx)]_0^\pi -\frac{4}{\pi^2}\left\{\left[\frac{x}{n}\sin (nx)\right]_0^\pi -\frac{1}{n}\int_0^\pi \sin (nx)dx\right\} \\ &=\frac{4}{n\pi^2}\int_0^\pi \sin (nx)dx \\ &=-\frac{4}{n^2\pi^2}\cos (nx)]_0^\pi \\ &=\frac{4}{n^2\pi ^2}(1-\cos (n\pi )).\end{aligned}\]
Since \[\cos (n\pi )=\left\{\begin{array}{rl}-1,& \text{if }n\text{ odd;} \\ 1,&\text{if }n\text{ even;}\end{array}\right.\nonumber\] we have \[a_n=\left\{\begin{array}{rl}8/(n^2\pi^2),&\text{if }n\text{ odd;} \\ 0,&\text{if }n\text{ even.}\end{array}\right.\nonumber\]
The Fourier cosine series for the triangle function is therefore given by \[f(x)=\frac{8}{\pi^2}\left(\cos x+\frac{\cos 3x}{3^2}+\frac{\cos 5x}{5^2}+\cdots\right).\nonumber\]
Convergence of this series is rapid. As an interesting aside, evaluation of this series at \(x = 0\), using \(f(0) = 1\), yields an infinite series for \(\pi^2/8\): \[\frac{\pi^2}{8}=1+\frac{1}{3^2}+\frac{1}{5^2}+\cdots\nonumber\]
With Fourier series now included in our applied mathematics toolbox, we are ready to solve the diffusion and wave equations in bounded domains.


