1.3E: Direction Fields for First Order Equations (Exercises)
- Page ID
- 18257
Exercises for Section 1.3
In Exercises 1–11 a direction field is drawn for the given equation. Sketch some integral curves.


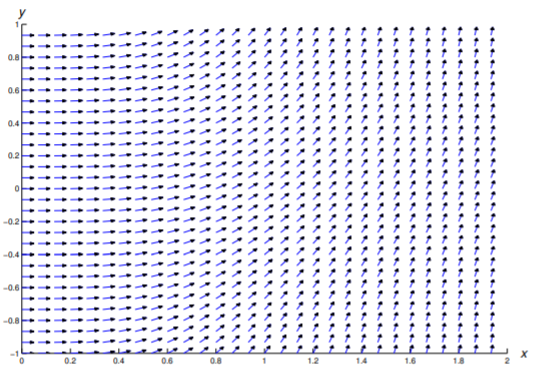
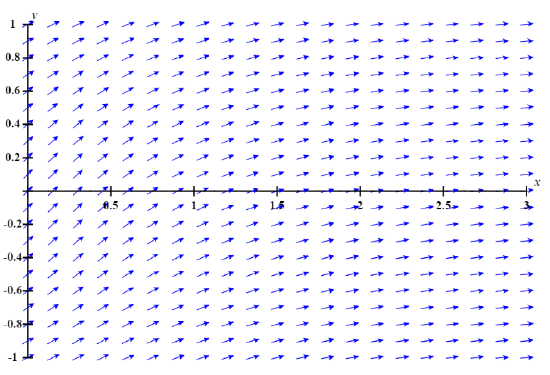

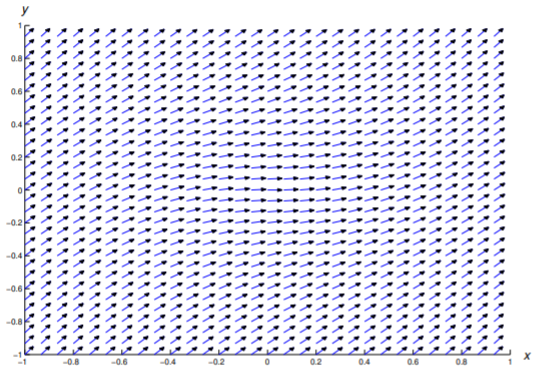
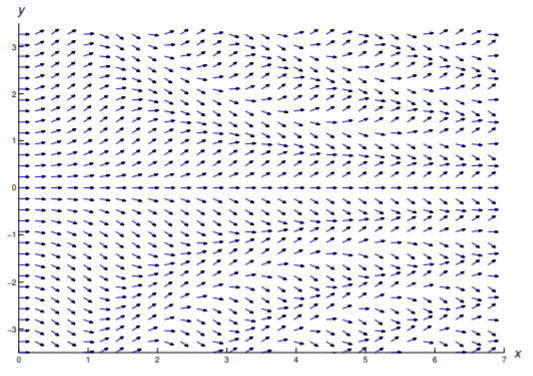
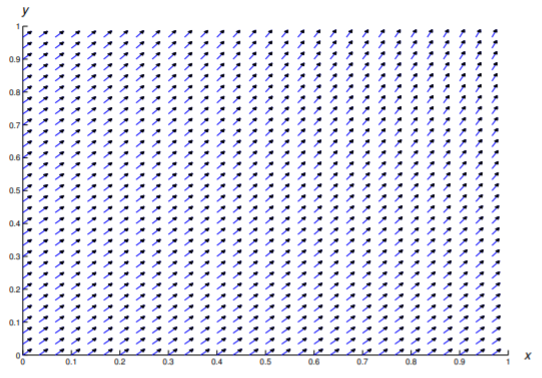
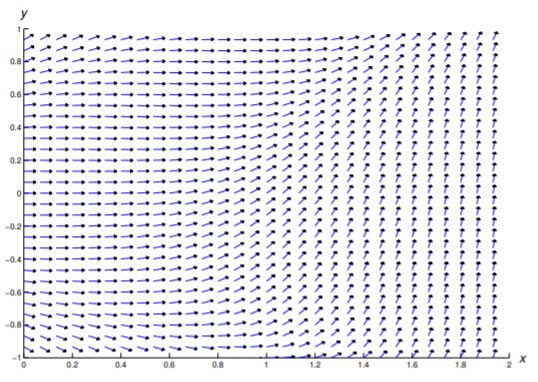
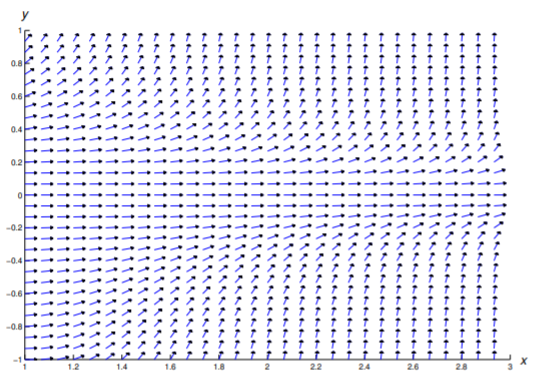

In Exercises 12 - 22 construct a direction field and plot some integral curves in the indicated rectangular region.
12. \(y'=y(y-1); \quad \{-1\le x\le 2,\ -2\le y\le2\}\)
13. \(y'=2-3xy; \quad \{-1\le x\le 4,\ -4\le y\le4\}\)
14. \(y'=xy(y-1); \quad \{-2\le x\le2,\ -4\le y\le 4\}\)
15. \(y'=3x+y; \quad \{-2\le x\le2,\ 0\le y\le 4\}\)
16. \(y'=y-x^3; \quad \{-2\le x\le2,\ -2\le y\le 2\}\)
17. \(y'=1-x^2-y^2; \quad \{-2\le x\le2,\ -2\le y\le 2\}\)
18. \(y'=x(y^2-1); \quad \{-3\le x\le3,\ -3\le y\le 2\}\)
19. \(y'= {x\over y(y^2-1)}; \quad \{-2\le x\le2,\ -2\le y\le 2\}\)
20. \(y'= {xy^2\over y-1}; \quad \{-2\le x\le2,\ -1\le y\le 4\}\)
21. \(y'= {x(y^2-1)\over y}; \quad \{-1\le x\le1,\ -2\le y\le 2\}\)
22. \(y'=- {x^2+y^2\over1-x^2-y^2}; \quad \{-2\le x\le2,\ -2\le y\le 2\}\)
23. By suitably renaming the constants and dependent variables in the equations
\[T' = -k(T-T_m) \tag{A}\]
and
\[G'=-\lambda G+r\tag{B}\]
discussed in Section 1.2 in connection with Newton’s law of cooling and absorption of glucose in the body, we can write both as
\[y'=- ay+b, \tag{C}\]
where \(a\) is a positive constant and \(b\) is an arbitrary constant. Thus, (A) is of the form (C) with \(y=T\), \(a=k\), and \(b=kT_m\), and (B) is of the form (C) with \(y=G\), \(a=\lambda\), and \(b=r\). We’ll encounter equations of the form (C) in many other applications in Chapter 2.
Choose a positive \(a\) and an arbitrary \(b\). Construct a direction field and plot some integral curves for (C) in a rectangular region of the form \[\{0\le t\le T,\ c\le y\le d\}\]
of the \(ty\)-plane. Vary \(T\), \(c\), and \(d\) until you discover a common property of all the solutions of (C). Repeat this experiment with various choices of \(a\) and \(b\) until you can state this property precisely in terms of \(a\) and \(b\).
24. By suitably renaming the constants and dependent variables in the equations
\[P'=aP(1-\alpha P) \tag{A}\]
and
\[I'=rI(S-I) \tag{B}\]
discussed in Section 1.1 in connection with Verhulst’s population model and the spread of an epidemic, we can write both in the form
\[y'=ay-by^2, \tag{C}\]
where \(a\) and \(b\) are positive constants. Thus, (A) is of the form (C) with \(y=P\), \(a=a\), and \(b=a\alpha\), and (B) is of the form (C) with \(y=I\), \(a=rS\), and \(b=r\). In Chapter 2 we’ll encounter equations of the form (C) in other applications..
Choose positive numbers \(a\) and \(b\). Construct a direction field and plot some integral curves for (C) in a rectangular region of the form \[\{0\le t\le T,\ 0\le y\le d\}\]
of the \(ty\)-plane. Vary \(T\) and \(d\) until you discover a common property of all solutions of (C) with \(y(0)>0\). Repeat this experiment with various choices of \(a\) and \(b\) until you can state this property precisely in terms of \(a\) and \(b\).
Choose positive numbers \(a\) and \(b\). Construct a direction field and plot some integral curves for (C) in a rectangular region of the form \[\{0\le t\le T,\ c\le y\le 0\}\]
of the \(ty\)-plane. Vary \(a\), \(b\), \(T\) and \(c\) until you discover a common property of all solutions of (C) with \(y(0)<0\).
You can verify your results later by doing Exercise 2.2.27.


