7.3.1: Boundary Value Problems: Dirichlet Problem

The Dirichlet problem (first boundary value problem) is to find a solution $u\in C^2(\Omega)\cap C(\overline{\Omega})$ of

$$\begin{eqnarray} \label{D1}\tag{7.3.1.1} \triangle u&=&0\ \ \mbox{in}\ \Omega\\ \label{D2}\tag{7.3.1.2} u&=&\Phi\ \ \mbox{on}\ \partial\Omega, \end{eqnarray}$$
where $\Phi$ is given and continuous on $\partial\Omega$.

Proposition 7.4. Assume $\Omega$ is bounded, then a solution to the Dirichlet problem is uniquely determined.

Proof. Maximum principle.

Remark. The previous result fails if we take away in the boundary condition ($\ref{D2}$) one point from the the boundary as the following example shows. Let $\Omega\subset\mathbb{R}^2$ be the domain
$$
\Omega=\{x\in B_1(0):\ x_2>0\},
\]

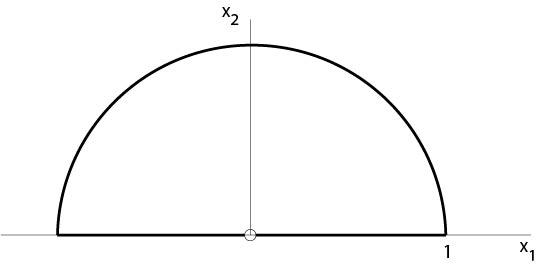
Figure 7.3.1.1: Counterexample

Assume $u\in C^2(\Omega)\cap C(\overline{\Omega}\setminus\{0\})$ is a solution of

$$\begin{eqnarray*} \triangle u&=&0\ \ \mbox{in}\ \Omega\\ u&=&0\ \ \mbox{on}\ \partial\Omega\setminus\{0\}. \end{eqnarray*}$$
This problem has solutions $u\equiv 0$ and $u=\mbox{Im}(z+z^{-1})$, where $z=x_1+ix_2$. Concerning another example see an exercise.

In contrast to this behavior of the Laplace equation, one has uniqueness if $\triangle u=0$ is replaced by the minimal surface equation
$$
\frac{\partial}{\partial x_1}\left(\frac{u_{x_1}}{\sqrt{1+|\nabla u|^2}}\right)+
\frac{\partial}{\partial x_2}\left(\frac{u_{x_2}}{\sqrt{1+|\nabla u|^2}}\right)=0.
\]

Contributors and Attributions

• Prof. Dr. Erich Miersemann (Universität Leipzig)

• Integrated by Justin Marshall.