3.3: Same sign lemmas
- Page ID
- 23593
Assume \(Q' \in [PQ)\) and \(Q' \ne P\). Then for any \(X \in (PQ)\) the angles \(PQX\) and \(PQ'X\) have the same sign.
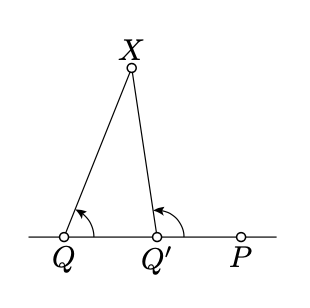
- Proof
-
By Proposition 2.2.2, for any \(t \in [0, 1]\) there is a unique point \(Q_t \in [PQ)\) such that
\[PQ_t = (1 - t) \cdot PQ + t \cdot PQ'.\]
Note that the map \(t \mapsto Q_t\) is continuous,
\(Q_0 = Q\), \(Q_1 = Q'\)
and for any \(t \in [0, 1]\), we have that \(P \ne Q_t\).
Applying Corollary 3.2.1, for \(P_t = P\), \(Q_t\), and \(X_t = X\), we get that \(\angle PQX\) has the same sign as \(\angle PQ'X\).
In arbitrary nondegenerate triangle \(ABC\), the angles \(ABC, BCA,\) and \(CAB\) have the same sign.
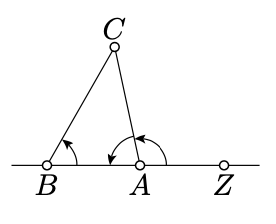
- Proof
-
Choose a point \(Z \in (AB)\) so that \(A\) lies between \(B\) and \(Z\).
According to Lemma \(\PageIndex{1}\), the angles \(ZBC\) and \(ZAC\) have the same sign.
Note that \(\measuredangle ABC = \measuredangle ZBC\) and
\[\measuredangle ZAC + \measuredangle CAB \equiv \pi.\]
Therefore, \(\angle CAB\) has the same sign as \(\angle ZAC\) which in turn has the same sign as \(\measuredangle ABC = \measuredangle ZBC\).
Repeating the same argument for \(\angle BCA\) and \(\angle CAB\), we get the result.
Assume \([XY]\) does not intersect \((PQ)\), then the angles \(PQX\) and \(PQY\) have the same sign.
The proof is nearly identical to the one above.
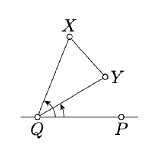
- Proof
-
According to Proposition 2.2.2, for any \(t \in [0, 1]\) there is a point \(X_t \in [XY]\), such that
\(XX_t = t \cdot XY.\)
Note that the map \(t \mapsto X_t\) is continuous. Moreover, \(X_0 = X\), \(X_1 = Y\), and \(X_t \not\in (QP)\) for any \(t \in [0, 1]\).
Applying Corollary 3.2.1, for \(P_t = P\), \(Q_t = Q\), and \(X_t\), we get that \(\angle PQX\) has the same sign as \(\angle PQY\).


