3.4: Half-planes
- Page ID
- 23594
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
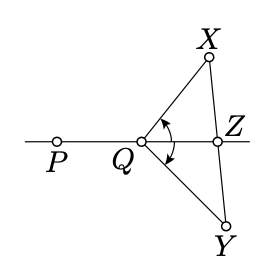
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Assume \(X, Y \not\in (PQ)\). Then the angles \(PQX\) and \(PQY\) have the same sign if and only if \([XY]\) does not intersect \((PQ)\).
- Proof
-
The if-part follows from Lemma 3.3.2.
Assume \([XY]\) intersects \((PQ)\); suppose that \(Z\) denotes the point of intersection. Without loss of generality, we can assume \(Z \ne P\).
Note that \(Z\) lies between \(X\) and \(Y\). According to Lemma 3.1.1, \(\angle PZX\) and \(\angle PZY\) have opposite signs. It proves the statement if \(Z = Q\).
If \(Z \ne Q\), then \(\angle ZQX\) and \(QZX\) have opposite signs by 3.7. The same way we get that \(\angle ZQY\) and \(\angle QZY\) have opposite signs.
If \(Q\) lies between \(Z\) and \(P\), then by Lemma 3.1.1 two pairs of angles \(\angle PQX\), \(\angle ZQX\) and \(\angle PQY\), \(\angle ZQY\) have opposite signs. It follows that \(\angle PQX\) and \(\angle PQY\) have opposite signs as required.
In the remaining case \([QZ) = [QP)\) and therefore \(\angle PQX = \angle ZQX\) and \(\angle PQY = \angle ZQY\). Therefore again \(\angle PQX\) and \(\angle PQY\) have opposite signs as required.
The complement of a line \((PQ)\) in the plane can be presented in a unique way as a union of two disjoint subsets called half-planes such that
(a) Two points \(X, Y \not\in (PQ)\) lie in the same half-plane if and only if the angles \(PQX\) and \(PQY\) have the same sign.
(b) Two points \(X, Y \not\in (PQ)\) in the same half-plane if and only if \([XY]\) does not intersect \((PQ)\).
We say that \(X\) and \(Y\) lie on one side of \((PQ)\) if they lie in one of the half-planes of \((PQ)\) and we say that \(P\) and \(Q\) lie on the opposite sides of \(l\) if they lie in the different half-planes of \(l\).
Exercise \(\PageIndex{1}\)
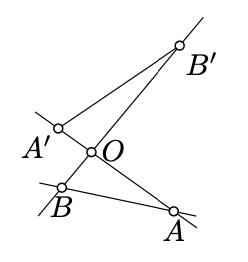
Suppose that the angles \(AOB\) and \(A'OB'\) are vertical and \(B \not\in (OA)\). Show that the line \((AB)\) does not intersect the segment \([A'B']\).
- Hint
-
Note that \(O\) and \(A'\) lie on the same side of \((AB)\). Analogously \(O\) and \(B'\) lie on the same side of \((AB)\). Hence the result.
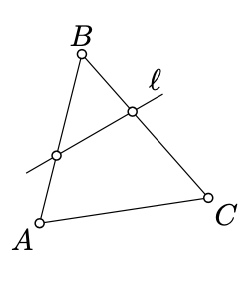
Consider the triangle \(ABC\). The segments \([AB], [BC]\), and \([CA]\) are called sides of the triangle.
Assume line \(l\) does not pass thru any vertex of a triangle. Then it intersects either two or zero sides of the triangle.
- Proof
-
Assume that the line \(l\) intersects side \([AB]\) of the triangle \(ABC\) and does not pass thru \(A, B,\) and \(C\).
By Corollary \(\PageIndex{1}\), the vertexes \(A\) and \(B\) lie on opposite sides of \(l\).
The vertex \(C\) may lie on the same side with \(A\) and on the opposite side with \(B\) or the other way around. By Corollary \(\PageIndex{1}\), in the first case, \(l\) intersects side \([BC]\) and does not intersect \([AC]\); in the second case, \(l\) intersects side \([AC]\) and does not intersect \([BC]\). Hence the statement follows.
Exercise \(\PageIndex{2}\)
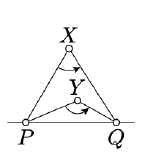
Show that two points \(X, Y \not\in (PQ)\) lie on the same side of \((PQ)\) if and only if the angles \(PXQ\) and \(PYQ\) have the same sign.
- Hint
-
Apply Theorem 3.3.1 for \(\triangle PQX\) and \(\triangle PQY\) and then apply Corollary \(\PageIndex{1}\)a.
Exercise \(\PageIndex{3}\)
Let \(\triangle ABC\) be a nondegenerate triangle, \(A' \in [BC]\) and \(B' \in [AC]\). Show that the segments \([AA']\) and \([BB']\) intersect.
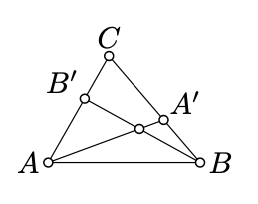
- Hint
-
We can assume that \(A' \ne B, C\) and \(B' \ne A, C\); otherwise the statement trivially holds.
Note that \((BB')\) does not intersect \([A'C]\). Applying Pasch's theorem (Theorem 3.4.1) for \(\triangle AA'C\) and \((BB')\), we get that \((BB')\) intersets \([AA']\); denote the point of intersection by \(M\).
The same way we get that \((AA')\) intersects \([BB']\); that is \(M\) lies on \([AA']\) and \([BB']\).
Exercise \(\PageIndex{4}\)
Assume that the points \(X\) and \(Y\) lie on opposite sides of the line \((PQ)\). Show that the half-line \([PX)\) does not intersect \([QY)\).
- Hint
-
Assume that \(Z\) is the point of intersection.
Note that \(Z \ne P\) and \(Z \ne Q\). Therefore, \(Z \in (PQ)\).
Show that \(Z\) and \(X\) lie on one side of \((PQ)\). Repeat the argument to show that \(Z\) and \(Y\) lie on one side of \((PQ)\). It follows that \(X\) and \(Y\) lie on the same side of \((PQ)\) - a contradiction.
Advanced Exercise \(\PageIndex{1}\)
Note that the follwing quantity
\[^{~} \measuredangle ABC = \begin{cases} \pi & \text{if } \measuredangle ABC = \pi \\ -\measuredangle ABC & \text{if } \measuredangle ABC < \pi \end{cases}\]
can serve as the angle measure; that is, the axioms hold if one exchanges \(\measuredangle\) to \(^{~} \measuredangle\) everywhere.
Show that \(\measuredangle\) and \(^{~} \measuredangle\) are the only possible angle measures on the plane.
Show that without Axiom IIIc, this is no longer true.


