6.2: Pythagorean theorem

Last updated
Save as PDF

Page ID: 23613

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A triangle is called right if one of its angles is right. The side opposite the right angle is called the hypotenuse. The sides adjacent to the right angle are called legs.

Theorem $\PageIndex{1}$

Assume $\triangle ABC$ is a right triangle with the right angle at $C$. Then

$AC^2 + BC^2 = AB^2.$

Proof

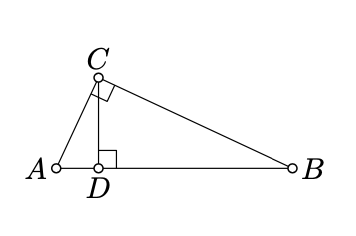
$截屏2021-02-08 上午10.52.32.png$

Let $D$ be the foot point of $C$ on $(AB)$.

According to Lemma 5.5.1,

$AD < AC < AB$

and

$BD < BC < AB.$

Therefore, $D$ lies between $A$ and $B$; in particular,

\[AD + BD = AB.\]

Note that by the AA similarity condition, we have

$\triangle ADC \sim \triangle ACB \sim \triangle CDB.$

In particular,

\[\dfrac{AD}{AC} = \dfrac{AC}{AB} \text{ and } \dfrac{BD}{BC} = \dfrac{BC}{BA}.\]

Let us rewrite the two identities in 6.2.2:

$AC^2 = AB \cdot AD$ and $BC^2 = AB \cdot BD$.

Summing up these two identities and applying 6.2.1, we get that

$AC^2 + BC^2 = AB \cdot (AD + BD) = AB^2.$

Exercise $\PageIndex{1}$

Assume $A, B, C$, and $D$ are as in the proof above. Show that

$CD^2 = AD \cdot BD.$

The following exercise is the converse to the Pythagorean theorem.

Hint: Apply that $\triangle ADC \sim \triangle CDB$.

Exercise $\PageIndex{2}$

Assume that $ABC$ is a triangle such that

$AC^2 + BC^2 = AB^2.$

Prove that the angle at $C$ is right.

Hint: Apply the Pythagorean theorem $\PageIndex{1}$ and the SSS congruence condition

Theorem \(\PageIndex{1}\)

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)