6.3: Method of similar triangles
( \newcommand{\kernel}{\mathrm{null}\,}\)
The proof of the Pythagorean theorem given above uses the method of similar triangles. To apply this method, one has to search for pairs of similar triangles and then use the proportionality of corresponding sides and/or equalities of corresponding angles. Finding such pairs might be tricky at first.
Let ABC be a nondegenerate triangle and the points X,Y, and Z as on the diagram. Assume ∡CAY≡∡XBC. Find four pairs of similar triangles with these six points as the vertexes and prove their similarity.
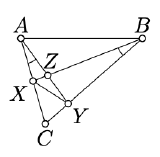
- Hint
-
By the AA similarity condition (Theorem 6.1.2), △AYC∼△BXC. Conclude that YCAC=XCBC. Apply the SAS similarity condition to show that △ABC∼△YXC.
Similarly, apply AA and equality of vertical angles to prove that △AZX∼△BZY and use SAS to show that △ABZ∼△YXZ.


