11.4: Defect
- Page ID
- 23650
The defect of triangle \(\triangle ABC\) is defined as
\(\text{defect} (\triangle ABC) := \pi - |\measuredangle ABC| - |\measuredangle BCA| - |\measuredangle CAB|.\)
Note that Theorem 11.3.1 states that the defect of any triangle in a neutral plane has to be nonnegative. According to Theorem 7.4.1, any triangle in the Euclidean plane has zero defect.
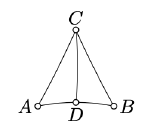
Let \(\triangle ABC\) be a nondegenerate triangle in the neutral plane. Assume \(D\) lies between \(A\) and \(B\). Show that
\(\text{defect} (\triangle ABC) = \text{defect} (\triangle ADC) + \text{defect} (\triangle DBC).\)
- Hint
-
Note that \(|\measuredangle ADC| + |\measuredangle CDB| = \pi\). Then apply the definition of the defect.
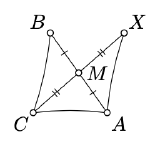
Let \(ABC\) be a nondegenerate triangle in the neutral plane. Suppose \(X\) is the reflection of \(C\) across the midpoint \(M\) of \([AB]\). Show that
\(\text{defect} (\triangle ABC) = \text{defect} (\triangle AXC).\)
- Hint
-
Show that \(\triangle AMX \cong \triangle BMC\). Apply Exercise \(\PageIndex{1}\) to \(\triangle ABC\) and \(\triangle AXC\).
Suppose that \(ABCD\) is a rectangle in a neutral plane; that is, \(ABCD\) is a quadrangle with all right angles. Show that \(AB = CD\).
- Hint
-
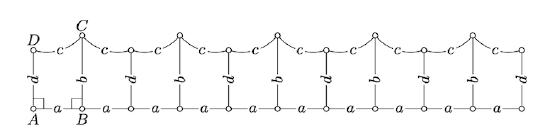
Show that \(B\) and \(D\) lie on the opposite sides of \((AC)\). Conclude that
\(\text{defect} (\triangle ABC) + \text{defect} (\triangle CDA) = 0.\)
Apply Theorem \(\PageIndex{1}\) to show that
\(\text{defect} (\triangle ABC) = \text{defect} (\triangle CDA = 0\)
Use it to show that \(\meauredangle CAB = \measuredangle ACD\) and \(\measuredangle ACB = \measuredangle CAD\). By ASA, \(\triangle ABC \cong \triangle CDA\), and, in particular, \(AB =CD\).
(Alternatively, you may apply Exercise 11.3.1)
Show that if a neutral plane has a rectangle, then all its triangles have zero defect.


