15.6: Moving points to infinity

Theorem 15.5.1 makes it possible to take any line in the projective plane and declare it to be ideal. In other words, we can choose a preferred affine plane by removing one line from the projective plane. This construction provides a method for solving problems in projective geometry which will be illustrated by the following classical example:

Theorem \(\PageIndex{1}\) Desargues' theorem

Desargues’ theorem[thm:desargues] Consider three concurrent lines \((AA')\), \((BB')\), and \((CC')\) in the real projective plane. Set

\(\begin{aligned} X&=(BC)\cap (B'C'),\\ Y&=(CA)\cap (C'A'),\\ Z&=(AB)\cap (A'B').\end{aligned}\)

Then the points \(X\), \(Y\), and \(Z\) are collinear.

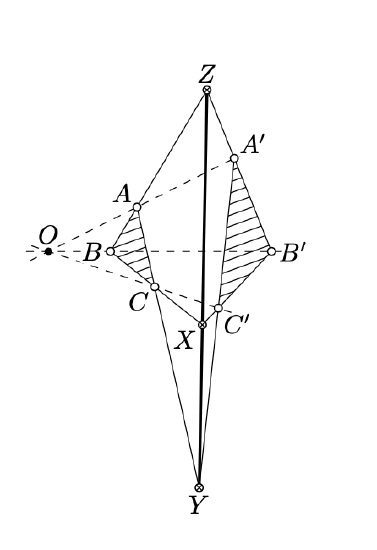
Proof

Without loss of generality, we may assume that the line \((XY)\) is ideal. If not, apply a perspective projection that sends the line \((XY)\) to the ideal line.

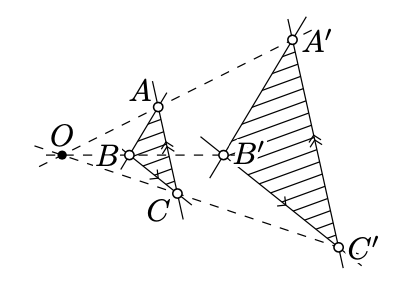
That is, we can assume that

\((BC) \parallel (B'C')\ \ \ \ \text{and} \ \ \ \ (CA) \parallel (C'A')\) 

and we need to show that

\((AB) \parallel(A'B').\)

Assume that the lines \((AA')\), \((BB')\), and \((CC')\) intersect at point \(O\). Since \((BC) \parallel (B'C')\), the transversal property (Theorem 7.3.1) implies that \(\measuredangle OBC = \measuredangle OB'C'\) and \(\measuredangle OCB = \measuredangle OC'B'\). By the AA similarity condition, \(\triangle OBC\z\sim\triangle OB'C'\). In particular,

\(\dfrac{OB}{OB'}=\dfrac{OC}{OC'}.\)

The same way we get that \(\triangle OAC \sim\triangle OA'C'\) and

\(\dfrac{OA}{OA'}=\dfrac{OC}{OC'}.\) 

Therefore,

\(\dfrac{OA}{OA'}=\dfrac{OB}{OB'}.\) 

By the SAS similarity condition, we get that \(\triangle OAB\sim\triangle OA'B'\); in particular, \(\measuredangle OAB = \pm\measuredangle OA'B'\).

Note that \(\measuredangle AOB=\measuredangle A'OB'\). Therefore,

\(\measuredangle OAB=\measuredangle OA'B'.\) 

By the transversal property (Theorem 7.3.1), we have \((AB)\parallel (A'B')\).

The case \((AA') \parallel (BB') \parallel (CC')\) is done similarly. In this case the quadrangles \(B'BCC'\) and \(A'ACC'\) are parallelograms. Therefore,

\(BB'=CC'=AA'.\)

Hence \(\square B'BAA'\) is a parallelogram and \((AB)\parallel (A'B')\).

Here is another classical theorem of projective geometry.

Theorem \(\PageIndex{2}\) Pappus' theorem

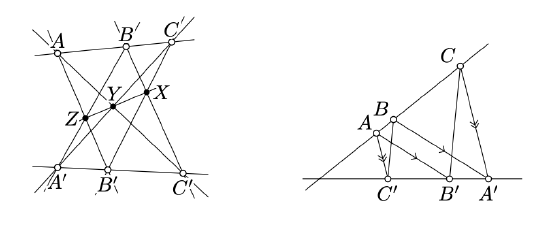
Assume that two triples of points \(A\), \(B\), \(C\), and \(A'\), \(B'\), \(C'\) are collinear. Suppose that points \(X\), \(Y\), \(Z\) are uniquely defined by

\(X = (BC') \cap (B'C)\),     \(Y = (CA') \cap (C'A)\),     \(Z = (AB') \cap (A'B).\)

Then the points \(X\), \(Y\), \(Z\) are collinear.

Pappus’ theorem can be proved the same way as Desargues’ theorem.

Idea of the Proof

Applying a perspective projection, we can assume that \(Y\) and \(Z\) lie on the ideal line. It remains to show that \(X\) lies on the ideal line.

In other words, assuming that \((AB') \parallel (A'B)\) and \((AC') \parallel (A'C)\), we need to show that \((BC') \parallel(B'C)\).

Exercise \(\PageIndex{1}\)

Finish the proof of Pappus’ theorem using the idea described above.

Hint

Assume that \((AB)\) meets \((A'B')\) at \(O\). Since \((AB') \parallel (BA')\), we get that \(\triangle OAB' \sim \triangle OBA'\) and \(\dfrac{OA}{OB} = \dfrac{OB'}{OA'}\).

Similarly, since \((AC') \parallel (CA')\), we get that \(\dfrac{OA}{OC} = \dfrac{OC'}{OA'}\).

Therefore \(\dfrac{OB}{OC} = \dfrac{OC'}{OB'}\). Applying the SAS similarity condition, we get that \(\triangle OBC' \sim \triangle OCB'\). Therefore, \((BC') \parallel (CB')\).

The case \((AB) \parallel (A'B')\) is similar.

The following exercise gives a partial converse to Pappus’ theorem.

Exercise \(\PageIndex{2}\)

Given two triples of points \(A\), \(B\), \(C\), and \(A'\), \(B'\), \(C'\), suppose distinct points \(X\), \(Y\), \(Z\) are uniquely defined by

\(\begin{aligned} X&=(BC')\cap(B'C), & Y&=(CA')\cap(C'A), & Z&=(AB')\cap(A'B).\end{aligned}\)

Assume that the triples \(A\), \(B\), \(C\), and \(X\), \(Y\), \(Z\) are collinear. Show that the triple \(A'\), \(B'\), \(C'\) is collinear.

Hint

Observe that the statement is equivalent to Pappus’ theorem.

Exercise \(\PageIndex{3}\)

Solve the following construction problem

1. using Desargues’ theorem;

2. using Pappus’ theorem.

Hint

To do (a), suppose that the parallelogram is formed by the two pairs of parallel lines \((AB) \parallel (A'B')\) and \((BC) \parallel (B'C')\) and \(\ell = (AC)\) in the notation of Desargues' theorem (Theorem \(\PageIndex{1}\))

To do (b), suppose that the parallelogram is formed by the two pairs of parallelogram is formed by the two pairs of parallel lines \((AB') \parallel (A'B')\) and \((BC') \parallel (B'C)\) and \(\ell = (AC')\) in the notation of Pappus' theorem (Theorem \(\PageIndex{2}\)).

Problem \(\PageIndex{1}\)

Suppose a parallelogram and a line \(\ell\) are given. Assume the line \(\ell\) crosses all sides (or their extensions) of the parallelogram at different points are given. Construct another line parallel to \(\ell\) with a ruler only.