7.3: Transversal Property

If the line \(t\) intersects each line \(\ell\) and \(m\) at one point, then we say that \(t\) is a transversal to \(\ell\) and \(m\). For example, on the diagram, line (\(CB\)) is a transversal to (\(AB\)) and (\(CD\)).

Theorem \(\PageIndex{1}\): Transversal Property

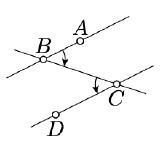
\((AB) \parallel (CD)\) if and only if

\[2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 0. \nonumber\]

Equivalently

\(\measuredangle ABC + \measuredangle BCD \equiv 0\) or \(\measuredangle ABC + \measuredangle BCD \equiv \pi.\)

Moreover, if \((AB) \ne (CD)\), then in the first case, \(A\) and \(D\) lie on opposite sides of \((BC)\); in the second case, \(A\) and \(D\) lie on the same sides of \((BC)\).

Proof

"only-if" part. Denote by \(O\) the midpoint of \([BC]\).

Assume \((AB) \parallel (CD)\). According to Theorem 7.2.1, \((CD)\) is a reflection of \((AB)\) across \(O\).

Let \(A'\) be the reflection of \(A\) across \(O\). Then \(A' \in (CD)\) and by Proposition 7.2.1 we have that

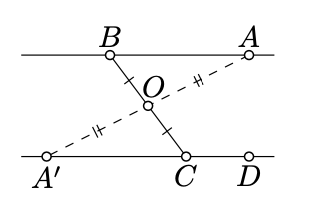
\[\measuredangle ABO = \measuredangle A'CO.\]

Note that

\[\measuredangle ABO \equiv \measuredangle ABC, \ \ \ \ \measuredangle A'CO \equiv \measuredangle BCA'.\]

Since \(A', C\) and \(D\) lie on one line, Exercise 2.4.2 implies that

\[2 \cdot \measuredangle BCD \equiv 2 \cdot \measuredangle BCA'.\]

Finally note that 7.3.2, 7.3.3 and 7.3.4 imply 7.3.1.

"If"-part. By Theorem 7.2.1 there is a unique line \((CD)\) thru \(C\) that is parallel to \((AB)\). From the "only-if" part we know that 7.3.1 holds.

On the other hand, there is a unique line \((CD)\) such that 7.3.1 holds. Indeed, suppose there are two such lines \((CD)\) and \((CD')\), then

\(2 \cdot (\measuredangle ABC + \measuredangle BCD) \equiv 2 \cdot (\measuredangle ABC + \measuredangle BCD') \equiv 0\).

Therefore \(2 \cdot \measuredangle BCD \equiv 2 \cdot BCD'\) and by Exercise 2.4.2, \(D' \in (CD)\), or equivalently the line \((CD)\) coincides with \((CD')\).

Therefore if 7.3.1 holds, then \((CD) \parallel (AB)\).

Finally, if \((AB) \ne (CD)\) and \(A\) and \(D\) lie on the opposite sides of \((BC)\), then \(\angle ABC\) and \(\angle BCD\) have opposite signs. Therefore

\(-\pi < \measuredangle ABC + \measuredangle BCD < \pi.\)

Applying 7.3.1, we get \(\measuredangle ABC + \measuredangle BCD = 0\).

Similarly if \(A\) and \(D\) lie on the same side of \((BC)\), then \(\angle ABC\) and \(\angle BCD\) have the same sign. Therefore

\(0 < |\measuredangle ABC + \measuredangle BCD| < 2\cdot \pi\)

and 7.3.1 implies that \(\measurdangle ABC + \measuredangle BCD \equiv \pi\).

Exercise \(\PageIndex{1}\)

Let \(\triangle ABC\) be a nondegenerate triangle, and \(P\) lies between \(A\) and \(B\). Suppose that a line \(\ell\) passes thru \(P\) and is parallel to \((AC)\). Show that \(\ell\) crosses the side \([BC]\) at another point, say \(Q\), and

\(\triangle ABC \sim \triangle PBQ.\)

In particular,

\(\dfrac{PB}{AB} = \dfrac{QB}{CB}.\)

Hint

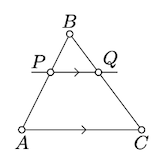
Since \(\ell \parallel (AC)\), it cannot cross \([AC]\). By Pasch's theorem (Theorem 3.4.1), \(\ell\) has to cross another side of \(\triangle ABC\). Therefore \(\ell\) cross \([BC]\); denote the point of intersection by \(Q\).

Use the transversal property (Theorem \(\PageIndex{1}\)) to show that \(\measuredangle BAC = \measuredangle BPQ\). The same argument shows that \(\measuredangel ACB = \measuredangle PQB\); it remains to apply the AA similarity condition.

Exercise \(\PageIndex{2}\)

Trisect a given segment with a ruler and a compass.

Answer

Assume we need to trisect segment \([AB]\). Construct a line \(\ell \ne (AB)\) with four points \(A, C_1, C_2, C_3\) such that \(C_1\) and \(C_2\) trisect \([AC_3]\). Draw the line \((BC_3)\) and draw parallel lines thru \(C_1\) and \(C_2\). The points of intersections of these two lines with \((AB)\) trisect the segment \([AB]\).