7.1: Parallel lines

In consequence of Axiom II, any two distinct lines $\ell$ and $m$ have either one point in common or none. In the first case they are intersecting (briefly $\ell \nparallel m$); in the second case, l and m are said to be parallel (briefly, $\ell \parallel m$); in addition, a line is always regarded as parallel to itself.

To emphasize that two lines on a diagram are parallel we will mark them with arrows of the same type.

Proposition $\PageIndex{1}$

Let $\ell, m$, and $n$ be three lines. Assume that $n \perp m$ and $m \perp \ell$. Then $\ell \parallel n$.

Proof

Assume the contrary; that is, $\ell \nparallel m$. Then there is a point, say $Z$, of intersection of $\ell$ and $n$. Then by Theorem 5.3.1, $\ell = n$. Since any line is parallel to itself, we have that $\ell \parallel n$ — a contradiction.

Theorem $\PageIndex{1}$

For any point $P$ and any line $\ell$ there is a unique line $m$ that passes thru $P$ and is parallel to $\ell$.

The above theorem has two parts, existence and uniqueness. In the proof of uniqueness we will use the method of similar triangles.

Proof

Apply Theorem 5.3.1 two times, first to construct the line $n$ thru $P$ that is perpendicular to $\ell$, and second to construct the line $n$ thru $P$ that is perpendicular to $m$. Then apply Proposition $\PageIndex{1}$.

Uniqueness. If $P \in \ell$, then $m =\ell$ by the definition of parallel lines. Further we assume $P \not\in \ell$.

Let us construct the lines $n \ni P$ and $m \ni P$ as in the proof of existence, so $m \parallel \ell$.

Assume there is yet another line $s \ni P$ parallel to $\ell$. Choose a point $Q \in s$ taht lies with $\ell$ on the same side from $m$. Let $R$ be the foot point of $Q$ on $n$.

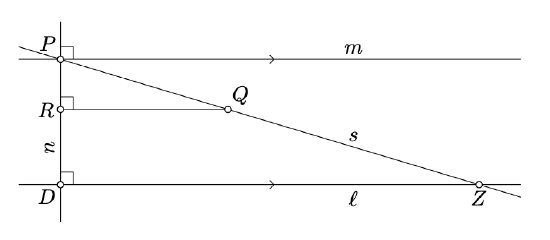
Let $D$ be the point of intersection of $n$ and $\ell$. According to Proposition $\PageIndex{1}$ $(QR) \parallel m$. Therefore, $Q, R$, and $\ell$ lie on the same side of $m$. In particular, $R \in [PD)$.

Choose $Z \in [PQ)$ such that

$\dfrac{PZ}{PQ} = \dfrac{PD}{PR}.$

By SAS similarity condition (or equivalently by Axiom V) we have that $\triangle RPQ \sim \triangle DPZ$; therefore $(ZD) \perp (PD)$. It follows that $Z$ lies on $\ell$ and $s$ - a condition.

Corollary $\PageIndex{2}$

Assume $\ell, m$, and $n$ are lines such that $\ell \parallel m$ and $m \parallel n$. Then $\ell \parallel n$.

Proof

Assume the contrary; that is, $\ell \nparallel n$. Then there is a point $P \in \ell \cap n$. By Theorem $\PageIndex{1}$, $n = \ell$ -- a contradiction.

Note that from the definition, we have that $\ell \parallel m$ if and only if $m \parallel \ell$. Therefore, according to the above corollary, "$\parallel$" is an equivalence relation. That is, for any lines $\ell, m$, and $n$ the following conditions hold:

(i) $\ell \parallel \ell$;
(ii) if $\ell \parallel m$, then $m \parallel \ell$;
(iii) if $\ell \parallel m$ and $m \parallel n$, then $\ell \parallel n$.

Exercise $\PageIndex{1}$

Let $k, \ell, m$, and $n$ be lines such that $k \perp \ell$, $\ell \perp m$, and $m \perp n$. Show that $k \nparallel n$.

Hint

Apply Proposition $\PageIndex{1}$ to show that $k \parallel m$. By Corollary $\PageIndex{2}$, $k \parallel n \Rightarrow m \parallel n$. The latter contradicts that $m \perp n$.

Exercise $\PageIndex{1}$

Make a ruler-and-compass construction of a line thru a given point that is parallel to a given line.

Hint

Repeat the construction in Exercise 5.7.1 twice.