19.2: Construtible numbers
- Page ID
- 23704
In the classical compass-and-ruler constructions initial configuration can be completely described by a finite number of points; each line is defined by two points on it and each circle is described by its center and a point on it (equivalently, you may describe a circle by three points on it).
The same way the result of construction can be described by a finite collection of points.
We may always assume that the initial configuration has at least two points; if not add one or two points to the configuration. Moreover, applying a scaling to the whole plane, we can assume that the first two points in the initial configuration lie at distance 1 from each other.
In this case we can choose a coordinate system, such that one of the initial points is the origin \((0,0)\) and yet another initial point has the coordinates \((1,0)\). In this coordinate system, the initial configuration of \(n\) points is described by \(2\cdot n-4\) numbers — their coordinates \(x_3,y_3,\dots,x_n,y_n\).
It turns out that the coordinates of any point constructed with a compass and ruler can be written thru the numbers \(x_3,y_3,\dots,x_n,y_n\) using the four arithmetic operations "\(+\)", "\(-\)", "\(\cdot\)", "\(/\)" and the square root "\(\sqrt{\phantom{a}}\)".
For example, assume we want to find the points \(X_1=(x_1,y_1)\) and \(X_2=(x_2,y_2)\) of the intersections of a line passing thru \(A=(x_A,y_A)\) and \(B=(x_B,y_B)\) and the circle with center \(O=(x_O,y_O)\) that passes thru the point \(W=(x_W,y_W)\). Let us write the equations of the circle and the line in the coordinates \((x,y)\):
Note that coordinates \((x_1,y_1)\) and \((x_2,y_2)\) of the points \(X_1\) and \(X_2\) are solutions of this system. Expressing \(y\) from the second equation and substituting the result in the first one, gives us a quadratic equation in \(x\), which can be solved using "\(+\)", "\(-\)", "\(\cdot\)", "\(/\)" and "\(\sqrt{\phantom{a}}\)" only.
The same can be performed for the intersection of two circles. The intersection of two lines is even simpler; it is described as a solution of two linear equations and can be expressed using only four arithmetic operations; the square root "\(\sqrt{\phantom{a}}\)" is not needed.
On the other hand, it is easy to make compass-and-ruler constructions that produce segments of the lengths \(a+b\) and \(a-b\) from two given segments of lengths \(a>b\).
To perform "\(\cdot\)", "\(/\)" and "\(\sqrt{\phantom{a}}\)" consider the following diagram: let \([AB]\) be a diameter of a circle; fix a point \(C\) on the circle and let \(D\) be the foot point of \(C\) on \([AB]\). By Corollary 9.3.1, the angle \(ACB\) is right. Therefore
\(\triangle ABC\sim\triangle ACD\sim \triangle CBD.\)
It follows that \(AD\cdot BD=CD^2\).
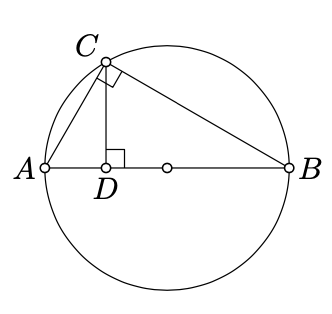
Using this diagram, one should guess a solution to the following exercise.
Given two line segments with lengths \(a\) and \(b\), give a ruler-and-compass construction of a segments with lengths \(\tfrac {a^2}b\) and \(\sqrt{a\cdot b}\).
- Hint
-
To construct \(\sqrt{a \cdot b}\): (1) construct points \(A, B\), and \(D \in [AB]\) such that \(AD = a\) and \(BD =b\); (2) construct the circle \(\Gamma\) on the diameter \([AB]\); (3) draw the line \(\ell\) thru \(D\) perpendicular to \((AB)\); (4) let \(C\) be an intersection of \(\Gamma\) and \(\ell\). Then \(DC = \sqrt{a \cdot b}\).
The construction of \(\dfrac{a^2}{b}\) is analogous.
Taking \(1\) for \(a\) or \(b\) above, we can produce \(\sqrt a\), \(a^2\), \(\tfrac1b\). Combining these constructions we can produce \(a\cdot b=(\sqrt{a\cdot b})^2\), \(\tfrac ab=a\cdot\tfrac 1b\). In other words we produced a compass-and-ruler calculator which can do "\(+\)", "\(-\)", "\(\cdot\)", "\(/\)", and "\(\sqrt{\phantom{a}}\)".
The discussion above gives a sketch of the proof of the following theorem:
Assume that the initial configuration of geometric construction is given by the points \(A_1=(0,0)\), \(A_2=(1,0)\), \(A_3=(x_3,y_3),\dots,A_n=(x_n,y_n)\). Then a point \(X=(x,y)\) can be constructed using a compass-and-ruler construction if and only if both coordinates \(x\) and \(y\) can be expressed from the integer numbers and \(x_3\), \(y_3\), \(x_4\), \(y_4,\dots,x_n,y_n\) using the arithmetic operations "\(+\)", "\(-\)", "\(\cdot\)", "\(/\)", and the square root "\(\sqrt{\phantom{a}}\)".
The numbers that can be expressed from the given numbers using the arithmetic operations and the square root “\(\sqrt{\phantom{a}}\)” are called constructible; if the list of given numbers is not given, then we can only use the integers.
The theorem above translates any compass-and-ruler construction problem into a purely algebraic language. For example:
- The impossibility of a solution for doubling the cube problem states that \(\sqrt[3]{2}\) is not a constructible number. That is \(\sqrt[3]{2}\) cannot be expressed thru integers using "\(+\)", "\(-\)", "\(\cdot\)", "\(/\)", and "\(\sqrt{\phantom{a}}\)".
- The impossibility of a solution for squaring the circle states that \(\sqrt{\pi}\), or equivalently \(\pi\), is not a constructible number.
- The Gauss–Wantzel theorem says for which integers \(n\) the number \(\cos\tfrac{2\cdot\pi}n\) is constructible.
Some of these statements might look evident, but rigorous proofs require some knowledge of abstract algebra (namely, field theory) which is out of the scope of this book.
In the next section, we discuss similar but simpler examples of impossible constructions with an unusual tool.
- Show that diagonal or regular pentagon is \(\tfrac{1+\sqrt5}2\) times larger than its side.
- Use (a) to make a compass-and-ruler construction of a regular pentagon.
- Hint
-
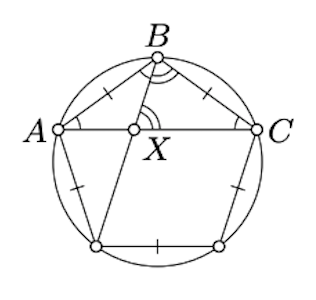
(a) Look at the diagram of regular pentagon; show that the angles marked the same way have the same angle measue. Conclude the that \(XC =BC\) and \(\triangle ABC \sim \triangle AXB\). Therefore
\(\dfrac{AB}{AC} = \dfrac{AX}{AB} = \dfrac{AC - AB}{AB} = \dfrac{AC}{AB} - 1\).
It remains to solve for \(\dfrac{AC}{AB}\).
(b) Choose two points \(P\) and \(Q\) and use the compass-and-ruler calculator to construct two points \(V\) and \(W\) such that \(VW = \dfrac{1 + \sqrt{5}}{2} \cdot PQ\). Then construct a pentagon with the sides \(PQ\) and diagonals \(VW\).


